Answer Key 10.6

  1. [latex]\phantom{a}[/latex]
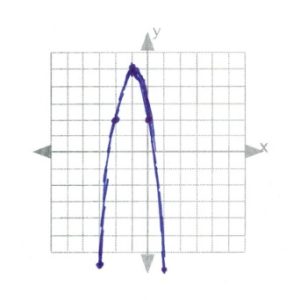
    [latex]\text{intercepts: }\begin{array}[t]{rrl} y&=&0 \\ 0&=&x^2-2x-8 \\ 0&=&(x-4)(x+2) \\ x&=&4,-2 \\ \\ \end{array}[/latex]
    [latex]\text{vertex: }\begin{array}[t]{l} \left[\dfrac{-b}{2a}, f\left(\dfrac{-b}{2a}\right)\right] \\ \\ (1,-9) \end{array}[/latex]
    [latex]\text{line of symmetry: }\begin{array}[t]{rll} x&=&\dfrac{-b}{2a} \\ \\ x&=& \dfrac{-(-2)}{2(1)}\Rightarrow \dfrac{2}{2}\text{ or }1 \\ \\ \therefore f(1)&=&1^2-2(1)-8 \\ \phantom{\therefore}f(1)&=&-9 \end{array}[/latex]
    Graph with line of symetry through x axis at 1
  2. [latex]\phantom{a}[/latex]
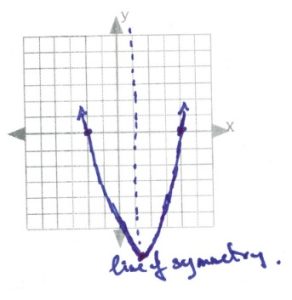
    [latex]\text{intercepts: }\begin{array}[t]{rrl} 0&=&x^2-2x-3 \\ 0&=&(x-3)(x+1) \\ x&=&3,-1 \end{array}[/latex]
    [latex]\text{line of symmetry: }\begin{array}[t]{rll} x&=& \dfrac{-(-2)}{2(1)}\Rightarrow \dfrac{2}{2}\text{ or }1 \end{array}[/latex]
    [latex]\text{vertex: }\begin{array}[t]{rll} f(1)&=&1^2-2(1)-3 \\ f(1)&=&1-2-3 \\ f(1)&=&-4 \\ \\ &&(1,-4) \end{array}[/latex]
    Graph with line of symmetry through (1,0)
  3. [latex]\phantom{a}[/latex]
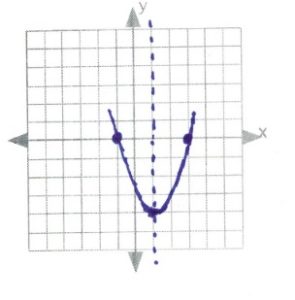
    [latex]\text{intercepts: }\begin{array}[t]{rrl} 0&=&2x^2-12x+10 \\ 0&=&2(x^2-6x+5) \\ 0&=&2(x-5)(x-1) \\ x&=&5,1 \end{array}[/latex]
    [latex]\text{line of symmetry: }\begin{array}[t]{rll} x&=&\dfrac{-b}{2a} \\ \\ x&=& \dfrac{-6}{2(1)}\Rightarrow \dfrac{6}{2}\text{ or }3 \end{array}[/latex]
    [latex]\text{vertex: }\begin{array}[t]{rll} f(3)&=&2(3)^2-12(3)+10 \\ f(3)&=&18-36+10 \\ f(3)&=&-8 \\ \\ &&(3,-8) \end{array}[/latex]
    Test of intercept with line of symmetry through x=3
  4. [latex]\phantom{a}[/latex]
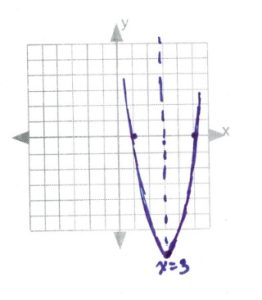
    [latex]\text{intercepts: }\begin{array}[t]{rrl} 0&=&2x^2-12x+16 \\ 0&=&2(x^2-6x+8) \\ 0&=&2(x-4)(x-2) \\ x&=&4,2 \end{array}[/latex]
    [latex]\text{line of symmetry: }\begin{array}[t]{rll} x&=&\dfrac{-b}{2a} \\ \\ x&=& \dfrac{-(-12)}{2(2)}\Rightarrow \dfrac{12}{4}\text{ or }3 \end{array}[/latex]
    [latex]\text{vertex: }\begin{array}[t]{rll} f(3)&=&2(3)^2-12(3)+16 \\ f(3)&=&18-36+16 \\ f(3)&=&-2 \\ \\ &&(3,-2) \end{array}[/latex]
    Line of symmetry through x=4
  5. [latex]\phantom{a}[/latex]
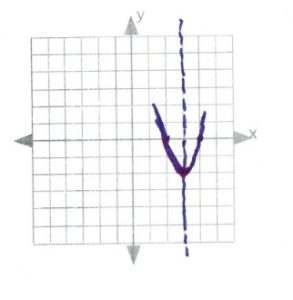
    [latex]\text{intercepts: }\begin{array}[t]{rrl} 0&=&-2x^2+12x-18 \\ 0&=&-2(x^2-6x+9) \\ 0&=&-2(x-3)(x-3) \\ x&=&3 \end{array}[/latex]
    [latex]\text{line of symmetry: }\begin{array}[t]{rll} x&=&\dfrac{-b}{2a} \\ \\ x&=& \dfrac{-12}{2(-2)}\Rightarrow \dfrac{-12}{-4}\text{ or }3 \end{array}[/latex]
    [latex]\text{vertex: }\begin{array}[t]{rll} f(3)&=&-2(3)^2-12(3)-18 \\ f(3)&=&-18+36-18 \\ f(3)&=&0 \\ \\ &&(0,3) \end{array}[/latex]
    Line of symmetry through x=4
  6. [latex]\phantom{a}[/latex]
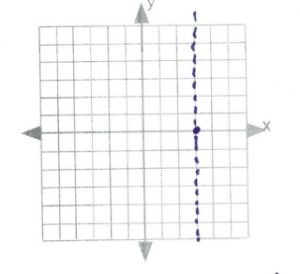
    [latex]\text{intercepts: }\begin{array}[t]{rrl} 0&=&-2x^2+12x-10 \\ 0&=&-2(x^2-6x+5) \\ 0&=&-2(x-5)(x-1) \\ x&=&5,1 \end{array}[/latex]
    [latex]\text{line of symmetry: }\begin{array}[t]{rll} x&=&\dfrac{-b}{2a} \\ \\ x&=& \dfrac{-12}{2(-2)}\Rightarrow \dfrac{-12}{-4}\text{ or }3 \end{array}[/latex]
    [latex]\text{vertex: }\begin{array}[t]{rll} f(3)&=&-2(3)^2-12(3)-10 \\ f(3)&=&-18+36-10 \\ f(3)&=&8 \\ \\ &&(3,8) \end{array}[/latex]
    Intercept test with line of symmetry through x=3
  7. [latex]\phantom{a}[/latex]
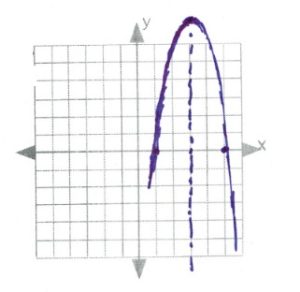
    [latex]\text{intercepts: }\begin{array}[t]{rrl} 0&=&-3x^2+24x-45 \\ 0&=&-3(x^2-8x+15) \\ 0&=&-3(x-3)(x-5) \\ x&=&3,5 \end{array}[/latex]
    [latex]\text{line of symmetry: }\begin{array}[t]{rll} x&=&\dfrac{-b}{2a} \\ \\ x&=& \dfrac{-24}{2(-3)}\Rightarrow \dfrac{-24}{-6}\text{ or }4 \end{array}[/latex]
    [latex]\text{vertex: }\begin{array}[t]{rll} f(4)&=&-3(4)^2+24(4)-45 \\ f(4)&=&-48+96-45 \\ f(4)&=&3 \\ \\ &&(4,3) \end{array}[/latex]
    Line of symmtery x=5
  8. [latex]\phantom{a}[/latex]
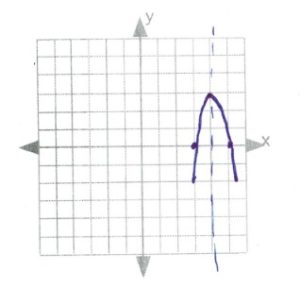
    [latex]\text{intercepts: }\begin{array}[t]{rrl} 0&=&-2(x^2+2x)+6 \\ 0&=&-2x^2-4x+6 \\ 0&=&-2(x^2+2x-3) \\ 0&=&-2(x+3)(x-1) \\ x&=&-3,1 \end{array}[/latex]
    [latex]\text{line of symmetry: }\begin{array}[t]{rll} x&=&\dfrac{-b}{2a} \\ \\ x&=& \dfrac{-(-4)}{2(-2)}\Rightarrow \dfrac{4}{-4}\text{ or }-1 \end{array}[/latex]
    [latex]\text{vertex: }\begin{array}[t]{rll} f(-1)&=&-2(-1)^2-4(-1)+6 \\ f(-1)&=&-2+4+6 \\ f(-1)&=&8 \\ \\ &&(-1,8) \end{array}[/latex]
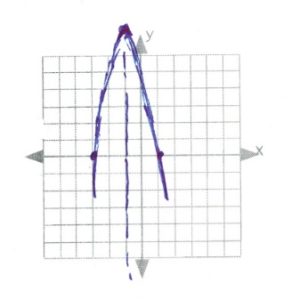
    Graph with line of symmetry x=-1
  9. [latex]\text{line of symmetry: }x=\dfrac{-b}{2a}\Rightarrow \dfrac{-(-6)}{2(3)}\Rightarrow \dfrac{6}{6}\text{ or }1[/latex]
    [latex]x[/latex] [latex]y[/latex]
    3 4
    2 −5
    1 −9
    0 −5
    −1 4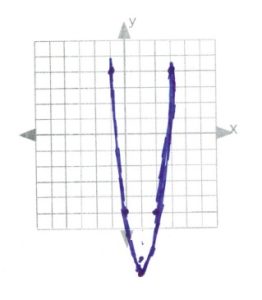

    Intercept test

  10. [latex]\text{line of symmetry: }x=\dfrac{-b}{2a}\Rightarrow \dfrac{-(-4)}{2(2)}\Rightarrow \dfrac{4}{4}\text{ or }1[/latex]
    [latex]x[/latex] [latex]y[/latex]
    3 3
    2 −3
    1 −5
    0 −3
    −1 3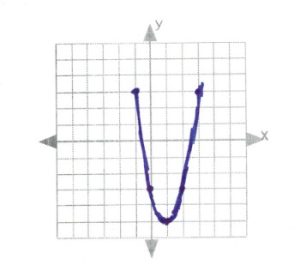

    Line of symmetry x=1

  11. [latex]\text{line of symmetry: }x=\dfrac{-b}{2a}\Rightarrow \dfrac{-4}{2(-1)}\Rightarrow \dfrac{-4}{-2}\text{ or }2[/latex]
    [latex]x[/latex] [latex]y[/latex]
    5 −3
    4 2
    3 5
    2 6
    1 5
    0 2
    −1 −3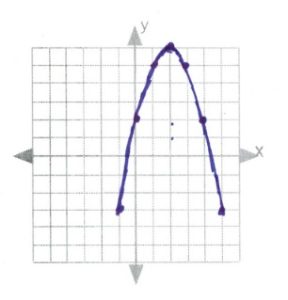

    Line of symmetry x=2

  12. [latex]\text{line of symmetry: }x=\dfrac{-b}{2a}\Rightarrow \dfrac{-(-6)}{2(-3)}\Rightarrow \dfrac{6}{-6}\text{ or }-1[/latex]
    [latex]x[/latex] [latex]y[/latex]
    1 −7
    0 2
    −1 5
    −2 2
    −3 −7

    Line of symmetry x=1

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Intermediate Algebra Copyright © 2020 by Terrance Berg is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book