Questions from Chapters 1 to 3

1. [latex]-(6)-\sqrt{6^2-4(4)(2)}[/latex]
   [latex]\begin{array}[t]{l}\\ -6-\sqrt{36-32} \\ \\ -6-\sqrt{4} \\ \\ -6-2=-8 \end{array}[/latex]
2. [latex]\phantom{a}[/latex]
   [latex]\begin{array}[t]{rrrrrrrrrrr} 6x&+&24&=&35&-&5x&-&8&+&12x \\ 6x&+&24&=&27&+&7x&&&& \\ -7x&-&24&&-24&-&7x&&&& \\ \hline &&-x&=&3&&&&&& \\ &&\therefore x&=&-3&&&&&& \\ \end{array}[/latex]
3. [latex]\left(\dfrac{x+4}{2}-\dfrac{1}{2}=\dfrac{x+2}{4}\right)(4)[/latex]
   [latex]\begin{array}[t]{crrrcrrrl} 2(x&+&4)&-&1(2)&=&x&+&2 \\ 2x&+&8&-&2&=&x&+&2 \\ -x&-&8&+&2&&-x&-&8+2 \\ \hline &&&&x&=&-4&& \end{array}[/latex]
4. [latex]x=-2[/latex]
5. [latex]\quad d^2=\Delta x^2+\Delta y^2[/latex]
   [latex]\begin{array}[t]{l} &=&(2--4)^2+(6--2)^2 \\ &=&6^2+8^2 \\ &=&36+64 \\ &=&100 \\ \\ \therefore d&=&\sqrt{100}=10 \end{array}[/latex]

6. [latex]2x-3y=6[/latex]

   [latex]x[/latex]	[latex]y[/latex]
   0	−2
   3	0
   6	2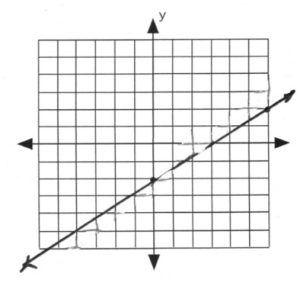

   

7. [latex]\phantom{a}[/latex]
   [latex]\begin{array}[t]{rrrrrrrrr} x&-&2x&+&10&\le &18&+&3x \\ &&-x&+&10&\le &18&+&3x \\ +&&-3x&-&10&&-10&-&3x \\ \hline &&&&\dfrac{-4x}{-4}&\le &\dfrac{8}{-4}&& \\ \\ &&&&x&\ge &-2&& \\ \end{array}[/latex]
   [latex][-2, \infty)[/latex]
   or equal to -2″ width=”300″ height=”69″>
8. [latex]\left(-1 < \dfrac{3x-2}{7}<1 \right)(7)[/latex] [latex]\begin{array}[t]{rrrcrrr} -7&<&3x&-&2&<&7 \\ +2&&&+&2&&+2 \\ \hline \dfrac{-5}{3}&<&&\dfrac{3x}{3}&&<&\dfrac{9}{3} \\ \\ -\dfrac{5}{3}&<&&x&&<&3 \end{array}[/latex] [latex]\phantom{1}[/latex] [latex]\left(-\dfrac{5}{3}, 3\right)[/latex]
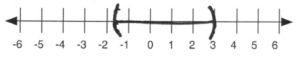
9. [latex]t=\dfrac{k}{r}[/latex]
   [latex]\begin{array}[t]{ll} \begin{array}[t]{rrl} &&\text{1st data} \\ \\ t&=&45\text{ min} \\ k&=&\text{find 1st} \\ r&=&600\text{ kL/min} \\ \\ t&=&\dfrac{k}{r} \\ \\ 45&=&\dfrac{k}{600} \\ \\ k&=&45(600) \\ k&=&27000\text{ kL} \end{array} & \hspace{0.25in} \begin{array}[t]{rrl} &&\text{2nd data} \\ \\ t&=&\text{find} \\ k&=&27000 \\ r&=&1000\text{ kL/min} \\ \\ t&=&\dfrac{k}{r} \\ \\ t&=&\dfrac{27000}{1000} \\ \\ t&=&27\text{ min} \end{array} \end{array}[/latex]
10. [latex]x, x+2[/latex]
    [latex]\begin{array}[t]{rrrrrrrrr} x&+&x&+&2&=&4(x)&-&12 \\ &&2x&+&2&=&4x&-&12 \\ &-&2x&+&12&&-2x&+&12 \\ \hline &&&&\dfrac{14}{2}&=&\dfrac{2x}{2}&& \\ \\ &&&&x&=&7&& \end{array}\\ \text{numbers are }7,9[/latex]

Questions from Chapters 4 to 6

1. [latex]\phantom{a}[/latex]
   [latex]\begin{array}[t]{rrrrrr} &2x&+&5y&=&-18 \\ +&-2x&+&y&=&6 \\ \hline &&&\dfrac{6y}{6}&=&\dfrac{-12}{6} \\ \\ &&&y&=&-2 \\ \\ &\therefore y&-&6&=&2x \\ &-2&-&6&=&2x \\ &&&2x&=&-8 \\ &&&x&=&-4 \end{array}[/latex]
   Answer: [latex](-4, -2)[/latex]
2. [latex]\phantom{a}[/latex]
   [latex]\begin{array}[t]{ll} \begin{array}[t]{rrrrrl} &(8x&+&7y&=&51)(-2) \\ &(5x&+&2y&=&20)(7) \\ \\ &-16x&-&14y&=&-102 \\ +&35x&+&14y&=&\phantom{-}140 \\ \hline &&&\dfrac{19x}{19}&=&\dfrac{38}{19} \\ \\ &&&x&=&2 \\ \\ \end{array} & \hspace{0.25in} \begin{array}[t]{rrrrr} \therefore 5x&+&2y&=&20 \\ 5(2)&+&2y&=&20 \\ 10&+&2y&=&20 \\ -10&&&&-10 \\ \hline &&2y&=&10 \\ &&y&=&5 \end{array} \end{array}[/latex]
   Answer: [latex](2, 5)[/latex]
3. [latex]\phantom{a}[/latex]
   [latex]\begin{array}[t]{ll} \begin{array}[t]{rrrrrrrl} &-2x&-&2y&-&12z&=&-10 \\ +&2x&&&-&3z&=&\phantom{-}4 \\ \hline &&&(-2y&-&15z&=&-6)(3) \\ &&&(3y&+&4z&=&\phantom{-}9)(2) \\ \\ &&&-6y&-&45z&=&-18 \\ &&+&6y&+&8z&=&\phantom{-}18 \\ \hline &&&&&-37z&=&0 \\ &&&&&z&=&0 \\ \\ \end{array} &\hspace{0.25in} \begin{array}[t]{rrrrl} 2x&-&\cancel{3z}0&=&4 \\ &&x&=&\dfrac{4}{2}\text{ or }2 \\ \\ 3y&+&\cancel{4z}0&=&9 \\ &&y&=&\dfrac{9}{3}\text{ or }3 \end{array} \end{array}[/latex]
   Answer [latex](2, 3, 0)[/latex]
4. [latex]24+\{-3x-\cancel{\left[6x-3(5-2x)\right]^0}1\}+3x[/latex]
   [latex]24-3x-1+3x[/latex]
   [latex]23[/latex]
5. [latex]2ab^3(a^2-16)\Rightarrow 2a^3b^3-32ab^3[/latex]
6. [latex](x^{1--2}y^{-3-4})^{-1}[/latex]
   [latex](x^3y^{-7})^{-1}[/latex]
   [latex]x^{-3}y^7 [/latex]
   [latex]\dfrac{y^7}{x^3}[/latex]
7. [latex]3x^2+3x+8x+8[/latex]
   [latex]3x(x+1)+8(x+1)[/latex]
   [latex](x+1)(3x+8)[/latex]
8. [latex](4x)^3-y^3\Rightarrow (4x-y)(16x^2+4xy+y^2)[/latex]
9. [latex]\phantom{a}[/latex]
   [latex]\begin{array}[t]{rrrcrl} &(A&+&B&=&\phantom{191.}50)(-370) \\ &(3.95A&+&3.70B&=&191.25)(100) \\ \\ &-370A&-&370B&=&-18500 \\ +&395A&+&370B&=&\phantom{-}19125 \\ \hline &&&25A&=&625 \\ \\ &&&A&=&\dfrac{625}{25}\text{ or }25 \\ \\ &A&+&B&=&50 \\ &25&+&B&=&50 \\ &&&B&=&25 \\ \end{array}[/latex]
10. [latex]\phantom{a}[/latex]
    [latex]\begin{array}[t]{rrrrrl} &(d&+&q&=&16)(-10) \\ &10d&+&25q&=&235 \\ \\ &-10d&-&10q&=&-160 \\ +&10d&+&25q&=&\phantom{-}235 \\ \hline &&&\dfrac{15q}{15}&=&\dfrac{75}{15} \\ \\ &&&q&=&5 \\ &&&\therefore d&=&16-5=11 \\ \end{array}[/latex]

Questions from Chapters 7 to 10

1. [latex]\dfrac{\cancel{15}3s^{\cancel{3}2}}{\cancel{3t^2}1}\cdot \dfrac{\cancel{17}1\cancel{s^3}}{\cancel{5}1\cancel{t}}\cdot \dfrac{\cancel{3t^3}}{\cancel{34}2\cancel{s^4}}\Rightarrow \dfrac{3s^2}{2}[/latex]
2. [latex]\text{LCD}=(x+2)(x-2)[/latex]
   [latex]\begin{array}[t]{l} \dfrac{2x(x-2)-4x(x+2)+20}{(x+2)(x-2)} \\ \\ \dfrac{2x^2-4x-4x^2-8x+20}{(x+2)(x-2)} \\ \\ \dfrac{-2x^2-12x+20}{(x+2)(x-2)} \\ \\ \dfrac{-2(x^2+6x-10)}{(x+2)(x-2)} \end{array}[/latex]
3. [latex]\dfrac{\left(\dfrac{x^2}{y^2}-9\right)y^3}{\left(\dfrac{x+3y}{y^3}\right)y^3}\Rightarrow \dfrac{x^2y-9y^3}{x+3y}\Rightarrow \dfrac{y(x^2-9y^2)}{x+3y}\Rightarrow \dfrac{y(x-3y)\cancel{(x+3y)}}{\cancel{(x+3y)}}[/latex]
   [latex]\Rightarrow y(x-3y)[/latex]
4. [latex]3\cdot 5\sqrt{x}-2\sqrt{36\cdot 2x}-\sqrt{16\cdot x^2\cdot x}[/latex]
   [latex]15\sqrt{x}-2\cdot 6\sqrt{2x}-4x\sqrt{x}[/latex]
   [latex]15\sqrt{x}-12\sqrt{2x}-4x\sqrt{x}[/latex]
5. [latex]\dfrac{\sqrt{m^6\cancel{n}}}{\sqrt{3\cancel{n}}}\Rightarrow \dfrac{m^3}{\sqrt{3}}\cdot \dfrac{\sqrt{3}}{\sqrt{3}}\Rightarrow \dfrac{m^3\sqrt{3}}{3}[/latex]
6. [latex]\left(\dfrac{\cancel{a^0}1b^4}{c^8d^{-12}}\right)^{\frac{1}{4}}\Rightarrow \dfrac{b^{4\cdot \frac{1}{4}}}{c^{8\cdot \frac{1}{4}}d^{-12\cdot \frac{1}{4}}}\Rightarrow \dfrac{b}{c^2d^{-3}}\Rightarrow \dfrac{bd^3}{c^2}[/latex]
7. [latex](x-5)(x+1)=0[/latex]
   [latex]x=5,-1[/latex]
8. [latex]\phantom{a}[/latex]
   [latex]\begin{array}[t]{rrrrrcrl} &&&(x&-&3)^2&=&(x)^2 \\ \\ &x^2&-&6x&+&9&=&\phantom{-}x^2 \\ -&x^2&&&&&&-x^2 \\ \hline &&&-6x&+&9&=&0 \\ \\ &&&&&\dfrac{-6x}{-6}&=&\dfrac{-9}{-6} \\ \\ &&&&&x&=&\dfrac{3}{2} \end{array}[/latex]
9. [latex]A\quad =\dfrac{1}{2}bh[/latex]
   [latex]\begin{array}[t]{rrl} 20&=&\dfrac{1}{2}(h+6)h \\ \\ 40&=&h^2+6h \\ \\ 0&=&h^2+6h-40 \\ 0&=&h^2+10h-4h-40 \\ 0&=&h(h+10)-4(h+10) \\ 0&=&(h-4)(h+10) \\ \\ h&=&4, \cancel{-10} \\ b&=&4+6=10 \end{array}[/latex]
10. [latex]x, x+2, x+4[/latex]
    [latex]\begin{array}[t]{rrrrcrrrlrrrr} &&&&x(x&+&2)&=&\phantom{-}8&+&6(x&+&4) \\ x^2&+&2x&&&&&=&\phantom{-}8&+&6x&+&24 \\ &-&6x&-&8&-&24&&-8&-&6x&-&24 \\ \hline &&x^2&-&4x&-&32&=&0&&&& \\ \\ x^2&+&4x&-&8x&-&32&=&0&&&& \\ x(x&+&4)&-&8(x&+&4)&=&0&&&& \\ &&(x&+&4)(x&-&8)&=&0&&&& \\ &&&&&&x&=&-4,8&&&&\\ \end{array}\\ \therefore \text{ numbers are }-4,-2,0 \text{ or } 8,10,12[/latex]