Chapter 4: Inequalities
4.1 Solve and Graph Linear Inequalities
When given an equation, such as [latex]x = 4[/latex] or [latex]x = -5,[/latex] there are specific values for the variable. However, with inequalities, there is a range of values for the variable rather than a defined value. To write the inequality, use the following notation and symbols:
| Symbol | Meaning |
|---|---|
| > Greater than | |
| ≤ Greater than or equal to | |
| < Less than | |
| ≥ Less than or equal to |
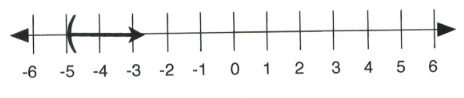
Example 4.1.1
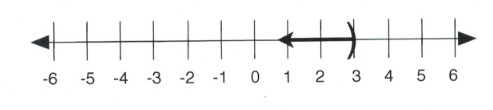
Given a variable [latex]x[/latex] such that [latex]x[/latex] > [latex]4[/latex], this means that [latex]x[/latex] can be as close to 4 as possible but always larger. For [latex]x[/latex] > [latex]4[/latex], [latex]x[/latex] can equal 5, 6, 7, 199. Even [latex]x =[/latex] 4.000000000000001 is true, since [latex]x[/latex] is larger than 4, so all of these are solutions to the inequality. The line graph of this inequality is shown below:

Written in interval notation, [latex]x[/latex] > [latex]4[/latex] is shown as [latex](4, \infty)[/latex].
Example 4.1.2
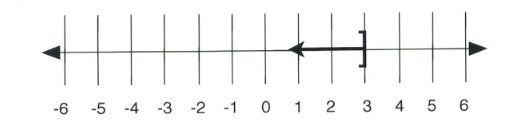
Likewise, if [latex]x < 3[/latex], then [latex]x[/latex] can be any value less than 3, such as 2, 1, −102, even 2.99999999999. The line graph of this inequality is shown below:
Written in interval notation, [latex]x < 3[/latex] is shown as [latex](-\infty, 3)[/latex].
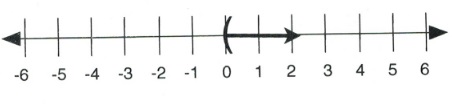
Example 4.1.3
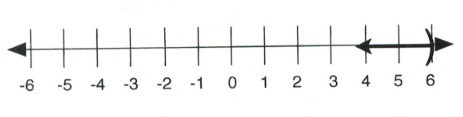
For greater than or equal (≥) and less than or equal (≤), the inequality starts at a defined number and then grows larger or smaller. For [latex]x \ge 4,[/latex] [latex]x[/latex] can equal 5, 6, 7, 199, or 4. The line graph of this inequality is shown below:

Written in interval notation, [latex]x \ge 4[/latex] is shown as [latex][4, \infty)[/latex].
Example 4.1.4
If [latex]x \le 3[/latex], then [latex]x[/latex] can be any value less than or equal to 3, such as 2, 1, −102, or 3. The line graph of this inequality is shown below:
Written in interval notation, [latex]x \le 3[/latex] is shown as [latex](-\infty, 3].[/latex]
When solving inequalities, the direction of the inequality sign (called the sense) can flip over. The sense will flip under two conditions:
First, the sense flips when the inequality is divided or multiplied by a negative. For instance, in reducing [latex]-3x < 12[/latex], it is necessary to divide both sides by −3. This leaves [latex]x[/latex] > [latex]-4.[/latex] Second, the sense will flip over if the entire equation is flipped over. For instance, [latex]x[/latex] > [latex]2[/latex], when flipped over, would look like [latex]2 < x.[/latex] In both cases, the 2 must be shown to be smaller than the [latex]x[/latex], or the [latex]x[/latex] is always greater than 2, no matter which side each term is on.
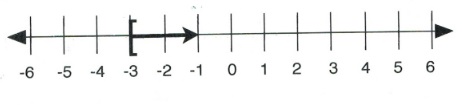
Example 4.1.5
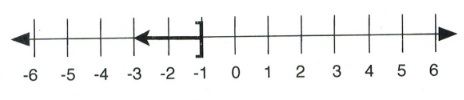
Solve the inequality [latex]5-2x[/latex] > [latex]11[/latex] and show the solution on both a number line and in interval notation.
First, subtract 5 from both sides:
[latex]\begin{array}{rrrrr} 5&-&2x&\ge &11 \\ -5&&&&-5 \\ \hline &&-2x&\ge &6 \end{array}[/latex]
Divide both sides by −2:
[latex]\begin{array}{rrr} \dfrac{-2x}{-2} &\ge &\dfrac{6}{-2} \\ \end{array}[/latex]
Since the inequality is divided by a negative, it is necessary to flip the direction of the sense.
This leaves:
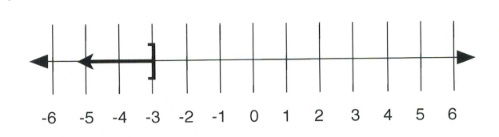
[latex]x \le -3[/latex]
In interval notation, the solution is written as [latex](-\infty, -3][/latex].
On a number line, the solution looks like:
Inequalities can get as complex as the linear equations previously solved in this textbook. All the same patterns for solving inequalities are used for solving linear equations.
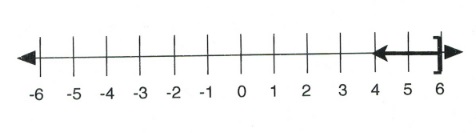
Example 4.1.6
Solve and give interval notation of [latex]3 (2x - 4) + 4x < 4 (3x - 7) + 8[/latex].
Multiply out the parentheses:
[latex]6x - 12 + 4x < 12x - 28 + 8[/latex]
Simplify both sides:
[latex]10x - 12 < 12x - 20[/latex]
Combine like terms:
[latex]\begin{array}{rrrrrrr} 10x&-&12&<&12x&-&20 \\ -12x&+&12&&-12x&+&12 \\ \hline &&-2x&<&-8&& \end{array}[/latex]
The last thing to do is to isolate [latex]x[/latex] from the −2. This is done by dividing both sides by −2. Because both sides are divided by a negative, the direction of the sense must be flipped.
This means:
[latex]\dfrac{-2x}{-2}< \dfrac{-8}{-2}[/latex]
Will end up looking like:
![]()
The solution written on a number line is:

Written in interval notation, [latex]x[/latex] > [latex]4[/latex] is shown as [latex](4, \infty)[/latex].
Questions
For questions 1 to 6, draw a graph for each inequality and give its interval notation.
- [latex]n[/latex] > [latex]-5[/latex]
- [latex]n[/latex] > [latex]4[/latex]
- [latex]-2 \le k[/latex]
- [latex]1 \ge k[/latex]
- [latex]5 \ge x[/latex]
- [latex]-5 < x[/latex]
For questions 7 to 12, write the inequality represented on each number line and give its interval notation.
For questions 13 to 38, draw a graph for each inequality and give its interval notation.
- [latex]\dfrac{x}{11}\ge 10[/latex]
- [latex]-2 \le \dfrac{n}{13}[/latex]
- [latex]2 + r < 3[/latex]
- [latex]\dfrac{m}{5} \le -\dfrac{6}{5}[/latex]
- [latex]8+\dfrac{n}{3}\ge 6[/latex]
- [latex]11[/latex] > [latex]8+\dfrac{x}{2}[/latex]
- [latex]2[/latex] > [latex]\dfrac{(a-2)}{5}[/latex]
- [latex]\dfrac{(v-9)}{-4} \le 2[/latex]
- [latex]-47 \ge 8 -5x[/latex]
- [latex]\dfrac{(6+x)}{12} \le -1[/latex]
- [latex]-2(3+k) < -44[/latex]
- [latex]-7n-10 \ge 60[/latex]
- [latex]18 < -2(-8+p)[/latex]
- [latex]5 \ge \dfrac{x}{5} + 1[/latex]
- [latex]24 \ge -6(m - 6)[/latex]
- [latex]-8(n - 5) \ge 0[/latex]
- [latex]-r -5(r - 6) < -18[/latex]
- [latex]-60 \ge -4( -6x - 3)[/latex]
- [latex]24 + 4b < 4(1 + 6b)[/latex]
- [latex]-8(2 - 2n) \ge -16 + n[/latex]
- [latex]-5v - 5 < -5(4v + 1)[/latex]
- [latex]-36 + 6x[/latex] > [latex]-8(x + 2) + 4x[/latex]
- [latex]4 + 2(a + 5) < -2( -a - 4)[/latex]
- [latex]3(n + 3) + 7(8 - 8n) < 5n + 5 + 2[/latex]
- [latex]-(k - 2)[/latex] > [latex]-k - 20[/latex]
- [latex]-(4 - 5p) + 3 \ge -2(8 - 5p)[/latex]