Midterm 1: Version B Answer Key
- [latex]-6-\sqrt{6^2-4(5)(1)} [/latex]
[latex]\begin{array}[t]{l}\\ -6-\sqrt{36-20} \\ \\ -6-\sqrt{16} \\ \\ -6-4 \\ \\ -10 \end{array}[/latex] - [latex]\phantom{a}[/latex]
[latex]\begin{array}[t]{rrrrrrrr} &15x&-&18&=&4[-6&+&3x] \\ &15x&-&18&=&-24&+&12x \\ -&12x&+&18&&+18&-&12x \\ \hline &&&\dfrac{3x}{3}&=&\dfrac{-6}{3} && \\ \\ &&&x&=&-2 && \end{array}[/latex] - [latex]\left(A=\dfrac{h}{B\cdot b}\right)(b)[/latex]
[latex]\begin{array}[t]{l}\\ \left(Ab=\dfrac{h}{B}\right)\div A \\ \\ \phantom{A}b=\dfrac{h}{BA} \end{array}[/latex] - [latex]\left(\dfrac{x+3}{5}-\dfrac{x}{2}=\dfrac{5-3x}{10}\right)(10)[/latex]
[latex]\begin{array}{rrcrcrrrr} 2(x&+&3)&-&5(x)&=&5&-&3x \\ 2x&+&6&-&5x&=&5&-&3x \\ &-&3x&+&6&=&5&-&3x \\ &+&3x&-&6&&-6&+&3x \\ \hline &&&&0&=&-1&&\\ \end{array}[/latex]
No solution - [latex]y=4[/latex]
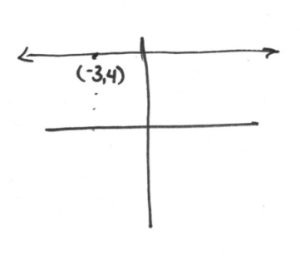
- [latex]\phantom{a}[/latex]
[latex]\begin{array}[t]{ll} \begin{array}[t]{rrl} \text{slope}&=&\dfrac{\Delta y}{\Delta x} \\ \\ \dfrac{1}{3}&=&\dfrac{y-4}{x--1} \end{array} & \hspace{0.25in} \begin{array}[t]{rrrrrrlrr} &&1(x&+&1)&=&3(y&-&4) \\ &&x&+&1&=&3y&-&12 \\ &&&-&1&&&-&1 \\ \hline &&&&x&=&3y&-&13 \\ \\ x&-&3y&+&13&=&0&& \\ \\ &&&&y&=&\dfrac{1}{3}x&+&\dfrac{13}{3} \end{array} \end{array}[/latex] - [latex]\text{1st slope }\dots\text{ } m=\dfrac{\Delta y}{\Delta x}\Rightarrow \dfrac{5-4}{-3-0}\Rightarrow -\dfrac{1}{3}[/latex]
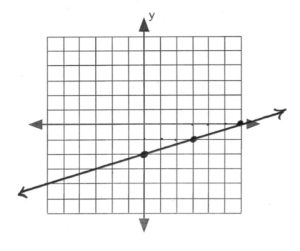
[latex]\text{now }\dots\text{ } m=\dfrac{\Delta y}{\Delta x}\Rightarrow -\dfrac{1}{3}\Rightarrow \dfrac{y-4}{x-0}[/latex]
[latex]\begin{array}{rrl} -1(x)&=&3(y-4) \\ -x&=&3y-12 \\ \\ x+3y-12&=&0 \\ y&=&-\dfrac{1}{3}x+4 \\ \end{array}[/latex] - [latex]\phantom{a}[/latex]
- [latex]\phantom{a}[/latex]
[latex]\begin{array}[t]{rrrrrrrrrrr} 6x&-&12&+&8x&>&15&-&20x&+&7 \\ &+&12&+&20x&&&+&20x&+&15 \\ &&&+&6x&&&&&+&12 \\ \hline &&&&34x&>&34&&&& \\ &&&&x&>&1&&&& \end{array}[/latex]
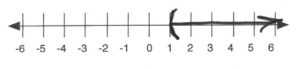1″ width=”300″ height=”69″> - [latex]\phantom{a}[/latex]
[latex]\begin{array}[t]{rrrcrrr} -3&\le &2x&+&3&<&9 \\ -3&&&-&3&&-3 \\ \hline \dfrac{-6}{2}&\le &&\dfrac{2x}{2}&&<&\dfrac{6}{2} \\ \\ -3&\le &&x&&<&3 \end{array}[/latex]
- [latex](-2<\dfrac{3x+2}{5}<2)(5)[/latex]
- [latex]\begin{array}{rrrrrrr} -10&<&3x&+&2&<&10 \\ -2&&&-&2&&-2 \\ \hline \dfrac{-12}{3}&<&&\dfrac{3x}{3}&&<&\dfrac{8}{3} \\ \\ -4&<&&x&&<&\dfrac{8}{3} \end{array}[/latex]
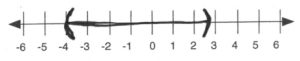
- [latex]\begin{array}{rrrrrrr} -10&<&3x&+&2&<&10 \\ -2&&&-&2&&-2 \\ \hline \dfrac{-12}{3}&<&&\dfrac{3x}{3}&&<&\dfrac{8}{3} \\ \\ -4&<&&x&&<&\dfrac{8}{3} \end{array}[/latex]
-
[latex]5x+2y=10[/latex] [latex]x[/latex] [latex]y[/latex] 2 0 0 5 −2 10 4 −5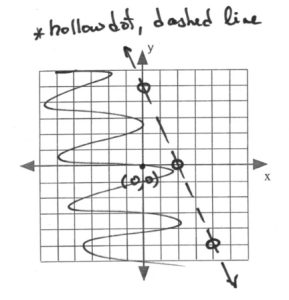 
- [latex]x, x+2[/latex]
[latex]\begin{array}{rrrrrrrrr} x&+&(x&+&2)&=&5x&-&16 \\ &&2x&+&2&=&5x&-&16 \\ &+&-5x&-&2&&-5x&-&2 \\ \hline &&&&\dfrac{-3x}{-3}&=&\dfrac{-18}{-3}&& \\ \\ &&&&x&=&6&& \\ \\ \end{array}[/latex]
numbers are 6, 8 - [latex]\phantom{a}[/latex]
[latex]\begin{array}[t]{rrl} 4x+x&=&40\text{ cm} \\ 5x&=&40\text{ cm} \\ x&=&\dfrac{40\text{ cm}}{5}\text{ or }8\text{ cm} \\ \\ \therefore 4x&=&4(8)\text{ or }32\text{ cm} \end{array}[/latex] - [latex]\phantom{a}[/latex]
[latex]\begin{array}[t]{ll} \begin{array}[t]{rrl} &&\underline{\text{1st}} \\ \\ P&=&\dfrac{kT}{V} \\ \\ &&\underline{\text{2nd}} \\ \\ &&\textbf{1st data} \\ P&=&100 \\ k&=&\text{find 1st} \\ T&=&200 \\ V&=&500 \\ \\ P&=&\dfrac{kT}{V} \\ \\ 100&=&\dfrac{k(200)}{500} \\ \\ k&=&\dfrac{\cancel{100}(500)}{\cancel{200}2} \\ \\ k&=&250 \end{array} & \hspace{0.25in} \begin{array}[t]{rrl} &&\textbf{2nd data} \\ P&=&\text{find 2nd} \\ k&=&250 \\ T&=&100 \\ V&=&500 \\ \\ P&=&\dfrac{kT}{V} \\ \\ P&=&\dfrac{(250)(100)}{500} \\ \\ P&=&50 \end{array} \end{array}[/latex]
