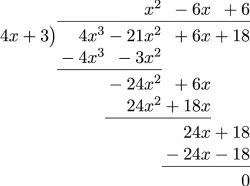Answer Key 6.7
- [latex]\phantom{a}[/latex]
[latex]\begin{array}[t]{ccccc} \dfrac{20x^4}{4x^3}&+&\dfrac{x^3}{4x^3}&+&\dfrac{2x^2}{4x^3} \\ \\ 5x&+&\dfrac{1}{4}&+&\dfrac{1}{2x} \end{array}[/latex] - [latex]\phantom{a}[/latex]
[latex]\begin{array}[t]{ccccc} \dfrac{5x^4}{9x}&+&\dfrac{45x^3}{9x}&+&\dfrac{4x^2}{9x} \\ \\ \dfrac{5}{9}x^3&+&5x^2&+&\dfrac{4}{9}x \end{array}[/latex] - [latex]\phantom{a}[/latex]
[latex]\begin{array}[t]{ccccc} \dfrac{20n^4}{10n}&+&\dfrac{n^3}{10n}&+&\dfrac{40n^2}{10n} \\ \\ 2n^3&+&\dfrac{n^2}{10}&+&4n \end{array}[/latex] - [latex]\phantom{a}[/latex]
[latex]\begin{array}[t]{ccccc} \dfrac{3k^3}{8k}&+&\dfrac{4k^2}{8k}&+&\dfrac{2k}{8k} \\ \\ \dfrac{3}{8}k^2&+&\dfrac{k}{2}&+&\dfrac{1}{4} \end{array}[/latex] - [latex]\phantom{a}[/latex]
[latex]\begin{array}[t]{ccccc} \dfrac{12x^4}{6x}&+&\dfrac{24x^3}{6x}&+&\dfrac{3x^2}{6x} \\ \\ 2x^3&+&4x^2&+&\dfrac{x}{2} \end{array}[/latex] - [latex]\phantom{a}[/latex]
[latex]\begin{array}[t]{ccccc} \dfrac{5p^4}{4p}&+&\dfrac{16p^3}{4p}&+&\dfrac{16p^2}{4p} \\ \\ \dfrac{5}{4}p^3&+&4p^2&+&4p \end{array}[/latex] - [latex]\phantom{a}[/latex]
[latex]\begin{array}[t]{ccccc} \dfrac{10n^4}{10n^2}&+&\dfrac{50n^3}{10n^2}&+&\dfrac{2n^2}{10n^2} \\ \\ n^2&+&5n&+&\dfrac{1}{5} \end{array}[/latex] - [latex]\phantom{a}[/latex]
[latex]\begin{array}[t]{ccccc} \dfrac{3m^4}{9m^2}&+&\dfrac{18m^3}{9m^2}&+&\dfrac{27m^2}{9m^2} \\ \\ \dfrac{m^2}{3}&+&2m&+&3 \end{array}[/latex] - [latex]\phantom{a}[/latex]
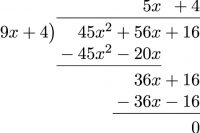
- [latex]\phantom{a}[/latex]
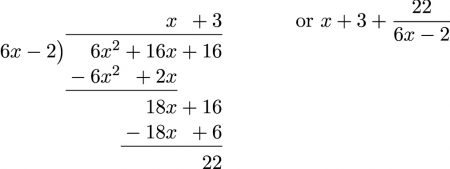
- [latex]\phantom{a}[/latex]
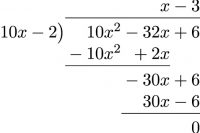
- [latex]\phantom{a}[/latex]
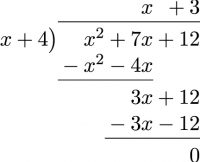
- [latex]\phantom{a}[/latex]
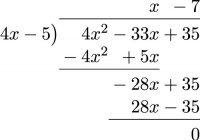
- [latex]\phantom{a}[/latex]
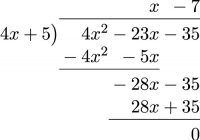
- [latex]\phantom{a}[/latex]
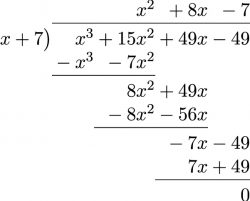
- [latex]\phantom{a}[/latex]
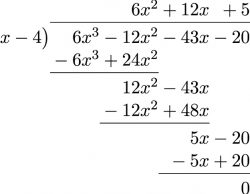
- [latex]\phantom{a}[/latex]

- [latex]\phantom{a}[/latex]
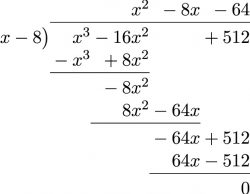
- [latex]\phantom{a}[/latex]
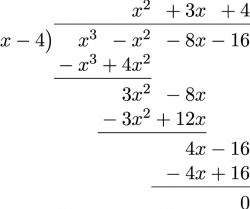
- [latex]\phantom{a}[/latex]
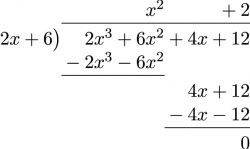
- [latex]\phantom{a}[/latex]
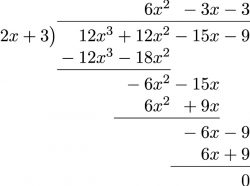
- [latex]\phantom{a}[/latex]