Answer Key 5.1
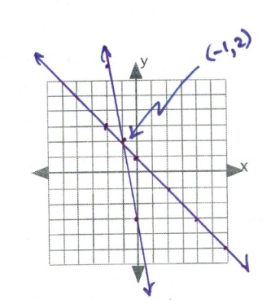
- [latex](-1,2)[/latex]
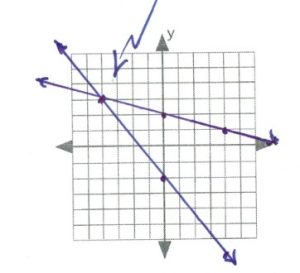
- [latex](-4,3)[/latex]
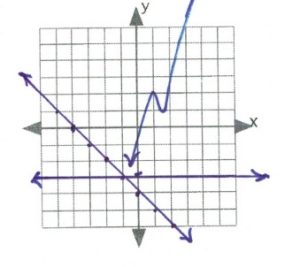
- [latex](-1,-3)[/latex]
- [latex](-3,1)[/latex]
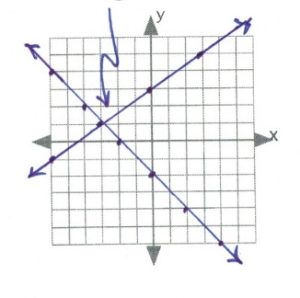
- Parallel lines [latex]\therefore[/latex] no intersection
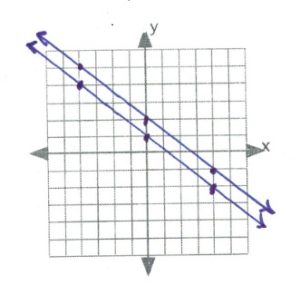
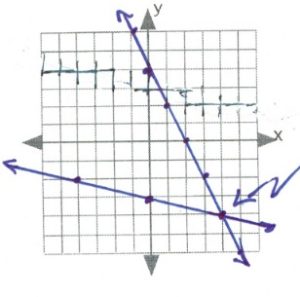
- [latex](-2,-2)[/latex]
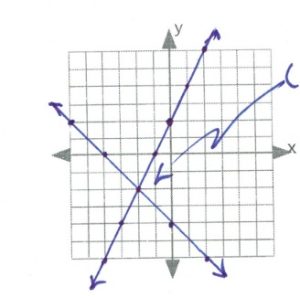
- [latex](-3,1)[/latex]
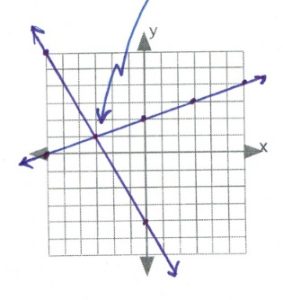
- [latex](1,-2)[/latex]
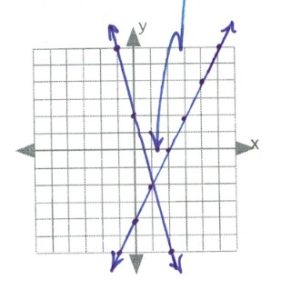
- [latex](-3,-1)[/latex]
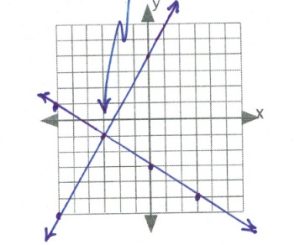
- Parallel lines [latex]\therefore[/latex] no intersection
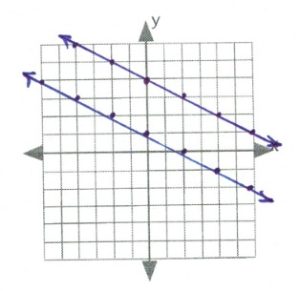
- [latex]\phantom{a}[/latex]
[latex]\begin{array}[t]{rrrrrrrrrr} x&+&3y&=&-9\hspace{0.25in}&5x&+&3y&=&3 \\ -x&&&&-x\hspace{0.25in}&-5x&&&&-5x \\ \hline \dfrac{3y}{3}&=&\dfrac{-x}{3}&-&\dfrac{9}{3}\hspace{0.25in}&\dfrac{3y}{3}&=&\dfrac{-5x}{3}&+&\dfrac{3}{3} \\ \\ y&=&-\dfrac{1}{3}x&-&3\hspace{0.25in}&y&=&-\dfrac{5}{3}x&+&1 \\ \\ (3,-4)&&&&&&&&& \end{array}[/latex]
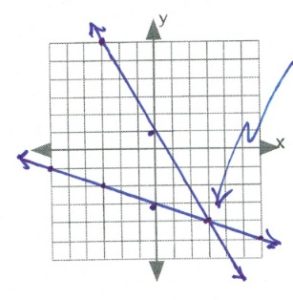
- [latex]\phantom{a}[/latex]
[latex]\begin{array}[t]{rrrrrrrrrr} x&+&4y&=&-12\hspace{0.25in}&2x&+&y&=&4 \\ -x&&&&-x\hspace{0.25in}&-2x&&&&-2x \\ \hline \dfrac{4y}{4}&=&\dfrac{-x}{4}&-&\dfrac{12}{4} \hspace{0.25in}&y&=&-2x&+&4 \\ \\ y&=&-\dfrac{1}{4}x&+&3 \hspace{0.25in}&y&=&-2x&+&4 \\ \\ (4,-4)&&&&&&&&& \end{array}[/latex]