Chapter 10: Quadratics
10.7 Quadratic Word Problems: Age and Numbers
Quadratic-based word problems are the third type of word problems covered in MATQ 1099, with the first being linear equations of one variable and the second linear equations of two or more variables. Quadratic equations can be used in the same types of word problems as you encountered before, except that, in working through the given data, you will end up constructing a quadratic equation. To find the solution, you will be required to either factor the quadratic equation or use substitution.
Example 10.7.1
The sum of two numbers is 18, and the product of these two numbers is 56. What are the numbers?
First, we know two things:
[latex]\begin{array}{l} \text{smaller }(S)+\text{larger }(L)=18\Rightarrow L=18-S \\ \\ S\times L=56 \end{array}[/latex]
Substituting [latex]18-S[/latex] for [latex]L[/latex] in the second equation gives:
[latex]S(18-S)=56[/latex]
Multiplying this out gives:
[latex]18S-S^2=56[/latex]
Which rearranges to:
[latex]S^2-18S+56=0[/latex]
Second, factor this quadratic to get our solution:
[latex]\begin{array}{rrrrrrl} S^2&-&18S&+&56&=&0 \\ (S&-&4)(S&-&14)&=&0 \\ \\ &&&&S&=&4, 14 \end{array}[/latex]
Therefore:
[latex]\begin{array}{l} S=4, L=18-4=14 \\ \\ S=14, L=18-14=4 \text{ (this solution is rejected)} \end{array}[/latex]
Example 10.7.2
The difference of the squares of two consecutive even integers is 68. What are these numbers?
The variables used for two consecutive integers (either odd or even) is [latex]x[/latex] and [latex]x + 2[/latex]. The equation to use for this problem is [latex](x + 2)^2 - (x)^2 = 68[/latex]. Simplifying this yields:
[latex]\begin{array}{rrrrrrrrr} &&(x&+&2)^2&-&(x)^2&=&68 \\ x^2&+&4x&+&4&-&x^2&=&68 \\ &&&&4x&+&4&=&68 \\ &&&&&-&4&&-4 \\ \hline &&&&&&\dfrac{4x}{4}&=&\dfrac{64}{4} \\ \\ &&&&&&x&=&16 \end{array}[/latex]
This means that the two integers are 16 and 18.
Example 10.7.3
The product of the ages of Sally and Joey now is 175 more than the product of their ages 5 years prior. If Sally is 20 years older than Joey, what are their current ages?
The equations are:
[latex]\begin{array}{rrl} (S)(J)&=&175+(S-5)(J-5) \\ S&=&J+20 \end{array}[/latex]
Substituting for S gives us:
[latex]\begin{array}{rrrrrrrrcrr} (J&+&20)(J)&=&175&+&(J&+&20-5)(J&-&5) \\ J^2&+&20J&=&175&+&(J&+&15)(J&-&5) \\ J^2&+&20J&=&175&+&J^2&+&10J&-&75 \\ -J^2&-&10J&&&-&J^2&-&10J&& \\ \hline &&\dfrac{10J}{10}&=&\dfrac{100}{10} &&&&&& \\ \\ &&J&=&10 &&&&&& \end{array}[/latex]
This means that Joey is 10 years old and Sally is 30 years old.
Questions
For Questions 1 to 12, write and solve the equation describing the relationship.
- The sum of two numbers is 22, and the product of these two numbers is 120. What are the numbers?
- The difference of two numbers is 4, and the product of these two numbers is 140. What are the numbers?
- The difference of two numbers is 8, and the sum of the squares of these two numbers are 320. What are the numbers?
- The sum of the squares of two consecutive even integers is 244. What are these numbers?
- The difference of the squares of two consecutive even integers is 60. What are these numbers?
- The sum of the squares of two consecutive even integers is 452. What are these numbers?
- Find three consecutive even integers such that the product of the first two is 38 more than the third integer.
- Find three consecutive odd integers such that the product of the first two is 52 more than the third integer.
- The product of the ages of Alan and Terry is 80 more than the product of their ages 4 years prior. If Alan is 4 years older than Terry, what are their current ages?
- The product of the ages of Cally and Katy is 130 less than the product of their ages in 5 years. If Cally is 3 years older than Katy, what are their current ages?
- The product of the ages of James and Susan in 5 years is 230 more than the product of their ages today. What are their ages if James is one year older than Susan?
- The product of the ages (in days) of two newborn babies Simran and Jessie in two days will be 48 more than the product of their ages today. How old are the babies if Jessie is 2 days older than Simran?
Example 10.7.4
Doug went to a conference in a city 120 km away. On the way back, due to road construction, he had to drive 10 km/h slower, which resulted in the return trip taking 2 hours longer. How fast did he drive on the way to the conference?
The first equation is [latex]r(t) = 120[/latex], which means that [latex]r = \dfrac{120}{t}[/latex] or [latex]t = \dfrac{120}{r}[/latex].
For the second equation, [latex]r[/latex] is 10 km/h slower and [latex]t[/latex] is 2 hours longer. This means the second equation is [latex](r - 10)(t + 2) = 120[/latex].
We will eliminate the variable [latex]t[/latex] in the second equation by substitution:
[latex](r-10)(\dfrac{120}{r}+2)=120[/latex]
Multiply both sides by [latex]r[/latex] to eliminate the fraction, which leaves us with:
[latex](r-10)(120+2r)=120r[/latex]
Multiplying everything out gives us:
[latex]\begin{array}{rrrrrrrrr} 120r&+&2r^2&-&1200&-&20r&=&120r \\ &&2r^2&+&100r&-&1200&=&120r \\ &&&-&120r&&&&-120r \\ \hline &&2r^2&-&20r&-&1200&=&0 \end{array}[/latex]
This equation can be reduced by a common factor of 2, which leaves us with:
[latex]\begin{array}{rrl} r^2-10r-600&=&0 \\ (r-30)(r+20)&=&0 \\ r&=&30\text{ km/h or }-20\text{ km/h (reject)} \end{array}[/latex]
Example 10.7.5
Mark rows downstream for 30 km, then turns around and returns to his original location. The total trip took 8 hr. If the current flows at 2 km/h, how fast would Mark row in still water?
If we let [latex]t =[/latex] the time to row downstream, then the time to return is [latex]8\text{ h}- t[/latex].
The first equation is [latex](r + 2)t = 30[/latex]. The stream speeds up the boat, which means [latex]t = \dfrac{30}{(r + 2)}[/latex], and the second equation is [latex](r - 2)(8 - t) = 30[/latex] when the stream slows down the boat.
We will eliminate the variable [latex]t[/latex] in the second equation by substituting [latex]t=\dfrac{30}{(r+2)}[/latex]:
[latex](r-2)\left(8-\dfrac{30}{(r+2)}\right)=30[/latex]
Multiply both sides by [latex](r + 2)[/latex] to eliminate the fraction, which leaves us with:
[latex](r-2)(8(r+2)-30)=30(r+2)[/latex]
Multiplying everything out gives us:
[latex]\begin{array}{rrrrrrrrrrr} (r&-&2)(8r&+&16&-&30)&=&30r&+&60 \\ &&(r&-&2)(8r&+&(-14))&=&30r&+&60 \\ 8r^2&-&14r&-&16r&+&28&=&30r&+&60 \\ &&8r^2&-&30r&+&28&=&30r&+&60 \\ &&&-&30r&-&60&&-30r&-&60 \\ \hline &&8r^2&-&60r&-&32&=&0&& \end{array}[/latex]
This equation can be reduced by a common factor of 4, which will leave us:
[latex]\begin{array}{rll} 2r^2-15r-8&=&0 \\ (2r+1)(r-8)&=&0 \\ r&=&-\dfrac{1}{2}\text{ km/h (reject) or }r=8\text{ km/h} \end{array}[/latex]
Questions
For Questions 13 to 20, write and solve the equation describing the relationship.
- A train travelled 240 km at a certain speed. When the engine was replaced by an improved model, the speed was increased by 20 km/hr and the travel time for the trip was decreased by 1 hr. What was the rate of each engine?
- Mr. Jones visits his grandmother, who lives 100 km away, on a regular basis. Recently, a new freeway has opened up, and although the freeway route is 120 km, he can drive 20 km/h faster on average and takes 30 minutes less time to make the trip. What is Mr. Jones’s rate on both the old route and on the freeway?
- If a cyclist had travelled 5 km/h faster, she would have needed 1.5 hr less time to travel 150 km. Find the speed of the cyclist.
- By going 15 km per hr faster, a transit bus would have required 1 hr less to travel 180 km. What was the average speed of this bus?
- A cyclist rides to a cabin 72 km away up the valley and then returns in 9 hr. His speed returning is 12 km/h faster than his speed in going. Find his speed both going and returning.
- A cyclist made a trip of 120 km and then returned in 7 hr. Returning, the rate increased 10 km/h. Find the speed of this cyclist travelling each way.
- The distance between two bus stations is 240 km. If the speed of a bus increases by 36 km/h, the trip would take 1.5 hour less. What is the usual speed of the bus?
- A pilot flew at a constant speed for 600 km. Returning the next day, the pilot flew against a headwind of 50 km/h to return to his starting point. If the plane was in the air for a total of 7 hours, what was the average speed of this plane?
Example 10.7.6
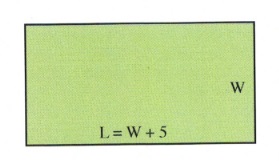
Find the length and width of a rectangle whose length is 5 cm longer than its width and whose area is 50 cm2.
First, the area of this rectangle is given by [latex]L\times W[/latex], meaning that, for this rectangle, [latex]L\times W=50[/latex], or [latex](W+5)W=50[/latex].
Multiplying this out gives us:
[latex]W^2+5W=50[/latex]
Which rearranges to:
[latex]W^2+5W-50=0[/latex]
Second, we factor this quadratic to get our solution:
[latex]\begin{array}{rrrrrrl} W^2&+&5W&-&50&=&0 \\ (W&-&5)(W&+&10)&=&0 \\ &&&&W&=&5, -10 \\ \end{array}[/latex]
We reject the solution [latex]W = -10[/latex].
This means that [latex]L = W + 5 = 5+5= 10[/latex].
Example 10.7.7
If the length of each side of a square is increased by 6, the area is multiplied by 16. Find the length of one side of the original square.
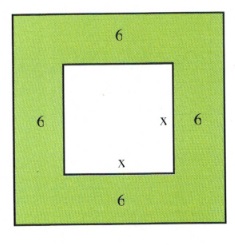 There are two areas to be considered: the area of the smaller square, which is [latex]x^2[/latex], and the area of the larger square, which is [latex](x + 12)^2[/latex].
There are two areas to be considered: the area of the smaller square, which is [latex]x^2[/latex], and the area of the larger square, which is [latex](x + 12)^2[/latex].
The relationship between these two is:
[latex]\begin{array}{rrl} \text{larger area}&=&16\text{ times the smaller area} \\ (x+12)^2&=&16(x)^2 \end{array}[/latex]
Simplifying this yields:
[latex]\begin{array}{rrrrrrr} x^2&+&24x&+&144&=&16x^2 \\ -16x^2&&&&&&-16x^2 \\ \hline -15x^2&+&24x&+&144&=&0 \end{array}[/latex]
Since this is a problem that requires factoring, it is easiest to use the quadratic equation:
[latex]x=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a},\hspace{0.25in}\text{ where }a=-15, b=24\text{ and }c=144[/latex]
Substituting these values in yields [latex]x = 4[/latex] or [latex]x=-2.4[/latex] (reject).
Example 10.7.8
Nick and Chloe want to surround their 60 by 80 cm wedding photo with matting of equal width. The resulting photo and matting is to be covered by a 1 m2 sheet of expensive archival glass. Find the width of the matting.
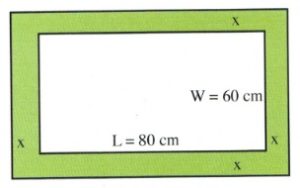 First, the area of this rectangle is given by [latex]L\times W[/latex], meaning that, for this rectangle:
First, the area of this rectangle is given by [latex]L\times W[/latex], meaning that, for this rectangle:
[latex](L+2x)(W+2x)=1\text{ m}^2[/latex]
Or, in cm:
[latex](80\text{ cm }+2x)(60\text{ cm }+2x)=10,000\text{ cm}^2[/latex]
Multiplying this out gives us:
[latex]4800+280x+4x^2=10,000[/latex]
Which rearranges to:
[latex]4x^2+280x-5200=0[/latex]
Which reduces to:
[latex]x^2 + 70x - 1300 = 0[/latex]
Second, we factor this quadratic to get our solution.
It is easiest to use the quadratic equation to find our solutions.
[latex]x=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a},\hspace{0.25in}\text{ where }a=1, b=70\text{ and }c=-1300[/latex]
Substituting the values in yields:
[latex]x=\dfrac{-70\pm \sqrt{70^2-4(1)(-1300)}}{2(1)}\hspace{0.5in}x=\dfrac{-70\pm 10\sqrt{101}}{2}[/latex]
[latex]x=-35+5\sqrt{101}\hspace{0.75in} x=-35-5\sqrt{101}\text{ (rejected)}[/latex]
Questions
For Questions 21 to 28, write and solve the equation describing the relationship.
- Find the length and width of a rectangle whose length is 4 cm longer than its width and whose area is 60 cm2.
- Find the length and width of a rectangle whose width is 10 cm shorter than its length and whose area is 200 cm2.
- A large rectangular garden in a park is 120 m wide and 150 m long. A contractor is called in to add a brick walkway to surround this garden. If the area of the walkway is 2800 m2, how wide is the walkway?
- A park swimming pool is 10 m wide and 25 m long. A pool cover is purchased to cover the pool, overlapping all 4 sides by the same width. If the covered area outside the pool is 74 m2, how wide is the overlap area?
- In a landscape plan, a rectangular flowerbed is designed to be 4 m longer than it is wide. If 60 m2 are needed for the plants in the bed, what should the dimensions of the rectangular bed be?
- If the side of a square is increased by 5 units, the area is increased by 4 square units. Find the length of the sides of the original square.
- A rectangular lot is 20 m longer than it is wide and its area is 2400 m2. Find the dimensions of the lot.
- The length of a room is 8 m greater than its width. If both the length and the width are increased by 2 m, the area increases by 60 m2. Find the dimensions of the room.

