Chapter 4: Inequalities

4.4 2D Inequality and Absolute Value Graphs

Graphing a 2D Inequality

To graph an inequality, borrow the strategy used to draw a line graph in 2D. To do this, replace the inequality with an equal sign.

Example 4.4.1

Consider the following inequalities:

[latex]\begin{array}{rrrrr}2x&+&2y&<&12 \\ 2x&+&2y&\le&12 \\2x&+&2y&>&12 \\2x&+&2y&\ge&12 \end{array}[/latex]

All can be changed to [latex]3x + 2y = 12[/latex] by replacing the inequality sign with =.

It is then possible to create a data table using the new equation.

Create a data table of values for the equation [latex]3x + 2y = 12.[/latex]

[latex]x[/latex] [latex]y[/latex]
0 6
2 3
4 0
6 −3

Using these values, plot the data points on a graph.

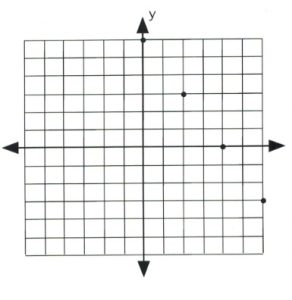
Graph. Points: (0, 6), (2, 3), (4, 0), and (6, −2).

Once the data points are plotted, draw a line that connects them all. The type of line drawn depends on the original inequality that was replaced.

If the inequality had ≤ or ≥, then draw a solid line to represent data points that are on the line.

Solid arrow going through solid dots.

If the inequality had < or >, then draw a dashed line instead to indicate that some data points are excluded.

Dashed arrow going through hollow dots.

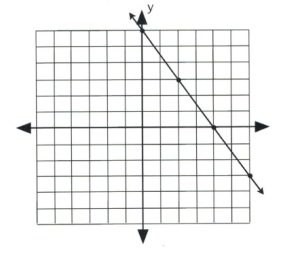
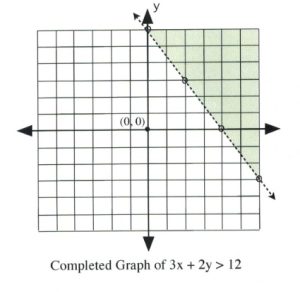
If the inequality is either [latex]3x + 2y \le 12[/latex] or [latex]3x + 2y \ge 12[/latex], then draw its graph using a solid line and solid dots.

Solid line with negative slope that passes through (0, 6) and (4, 0).

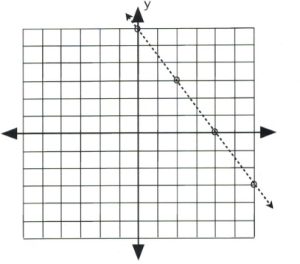
If the inequality is either [latex]3x + 2y < 12[/latex] or [latex]3x + 2y[/latex] > [latex]12[/latex], then draw its graph using a dashed line and hollow dots. Dashed line with negative slope that passes through (0, 6) and (4, 0).

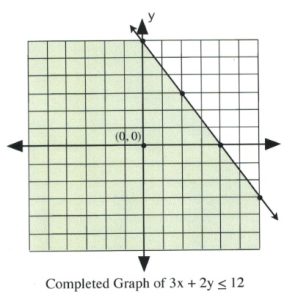
There remains only one step to complete this graph: finding which side of the line makes the inequality true and shading it. The easiest way to do this is to choose the data point [latex](0, 0)[/latex].

It is evident that, for [latex]3(0) + 2(0) \le 12[/latex] and [latex]3(0) + 2(0) < 12[/latex], the data point [latex](0, 0)[/latex] is true for the inequality. In this case, shade the side of the line that contains the data point [latex](0, 0)[/latex]. Completed graph of 3x + 2y ≤ 12. The side with (0, 0) is shaded.

It is also clear that, for [latex]3(0) + 2(0) \ge 12[/latex] and [latex]3(0) + 2(0)[/latex] > [latex]12[/latex], the data point [latex](0, 0)[/latex] is false for the inequality. In this case, shade the side of the line that does not contain the data point [latex](0, 0)[/latex].

Completed graph of 3x + 2y is greater than 12. The side without (0, 0) is shaded.

Graphing an Absolute Value Function

To graph an absolute value function, first create a data table using the absolute value part of the equation.

The data point that is started with is the one that makes the absolute value equal to 0 (this is the [latex]x[/latex]-value of the vertex). Calculating the value of this point is quite simple.

For example, for [latex]| x - 3 |[/latex], the value [latex]x = 3[/latex] makes the absolute value equal to 0.

Examples of others are:

[latex]\begin{array}{rrrrrrrrr} |x&+&2|&=&0&\text{when}&x&=&-2 \\ |x&-&11|&=&0&\text{when}&x&=&11 \\ |x&+&9|&=&0&\text{when}&x&=&-9 \\ \end{array}[/latex]

The graph of an absolute value equation will be a V-shape that opens upward for any positive absolute function and opens downward for any negative absolute value function.

Example 4.4.2

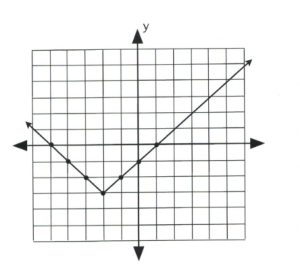
Plot the graph of [latex]y = | x + 2 | - 3.[/latex]

The data point that gives the [latex]x[/latex]-value of the vertex is [latex]| x + 2 | = 0,[/latex] in which [latex]x = -2.[/latex] This is the first value.

For [latex]x = -2, y = | -2 + 2 | - 3,[/latex] which yields [latex]y = -3.[/latex]

Now pick [latex]x[/latex]-values that are larger and less than −2 to get three data points on both sides of the vertex, [latex](-2, -3).[/latex]

[latex]x[/latex] [latex]y[/latex]
1 0
0 −1
−1 −2
−2 −3
−3 −2
−4 −1
−5 0

Once there are three data points on either side of the vertex, plot and connect them in a line. The graph is complete.

Positive absolute value graph that goes through (−5, 0), (0, −1) and (1, 0). Vertex is (−2, −3).

Example 4.4.3

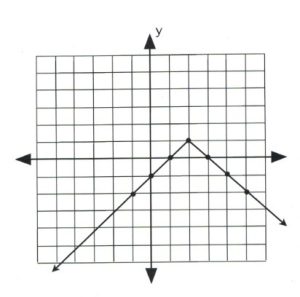
Plot the graph of [latex]y = -| x - 2 | + 1.[/latex]

The data point that gives the [latex]x[/latex]-value of the vertex is [latex]| x - 2 | = 0,[/latex] in which [latex]x = 2.[/latex] This is the first value.

For [latex]x = 2, y = -| 2 - 2 | + 1,[/latex] which yields [latex]y = 1.[/latex]

Now pick [latex]x[/latex]-values that are larger and less than 2 to get three data points on both sides of the vertex, [latex](2, 1).[/latex]

[latex]x[/latex] [latex]y[/latex]
5 −2
4 −1
3 0
2 1
1 0
0 −1
−1 −2

Once there are three data points on either side of the vertex, plot and connect them in a line. The graph is complete.

Negative absolute value graph with vertex (2, 1). Goes through (0, −1), (1, 0) and (3, 0).

Questions

For questions 1 to 8, graph each linear inequality.

  1. [latex]y[/latex] > [latex]3x + 2[/latex]
  2. [latex]3x - 4y[/latex] > [latex]12[/latex]
  3. [latex]2y \ge 3x + 6[/latex]
  4. [latex]3x - 2y \ge 6[/latex]
  5. [latex]2y[/latex] > [latex]5x + 10[/latex]
  6. [latex]5x + 4y[/latex] > [latex]-20[/latex]
  7. [latex]4y \ge 5x + 20[/latex]
  8. [latex]5x + 2y \ge -10[/latex]

For questions 9 to 16, graph each absolute value equation.

  1. [latex]y=|x-4|[/latex]
  2. [latex]y=|x-3|+3[/latex]
  3. [latex]y=|x-2|[/latex]
  4. [latex]y=|x-2|+2[/latex]
  5. [latex]y=-|x-2|[/latex]
  6. [latex]y=-|x-2|+2[/latex]
  7. [latex]y=-|x+2|[/latex]
  8. [latex]y=-|x+2|+2[/latex]

Answer Key 4.4

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Intermediate Algebra Copyright © 2020 by Terrance Berg is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book