Chapter 3: Graphing
3.2 Midpoint and Distance Between Points
Finding the Distance Between Two Points
The logic used to find the distance between two data points on a graph involves the construction of a right triangle using the two data points and the Pythagorean theorem [latex](a^2 + b^2 = c^2)[/latex] to find the distance.
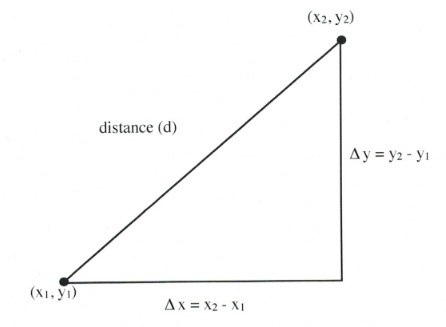
To do this for the two data points [latex](x_1, y_1)[/latex] and [latex](x_2, y_2)[/latex], the distance between these two points [latex](d)[/latex] will be found using [latex]\Delta x = x_2 - x_1[/latex] and [latex]\Delta y = y_2 - y_1.[/latex]
Using the Pythagorean theorem, this will end up looking like:
[latex]d^2 = \Delta x^2 + \Delta y^2[/latex]
or, in expanded form:
[latex]d^2 = (x_2 - x_1)^2 + (y_2 - y_1)^2[/latex]
On graph paper, this looks like the following. For this illustration, both [latex]\Delta x[/latex] and [latex]\Delta y[/latex] are 7 units long, making the distance [latex]d^2 = 7^2 + 7^2[/latex] or [latex]d^2 = 98[/latex].
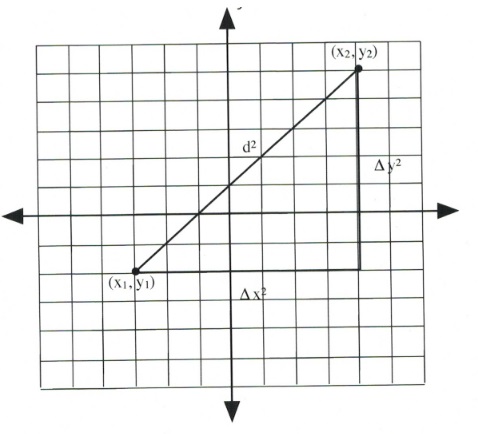
The square root of 98 is approximately 9.899 units long.
Example 3.2.1
Find the distance between the points [latex](-6,-4)[/latex] and [latex](6, 5)[/latex].
Start by identifying which are the two data points [latex](x_1, y_1)[/latex] and [latex](x_2, y_2)[/latex]. Let [latex](x_1, y_1)[/latex] be [latex](-6,-4)[/latex] and [latex](x_2, y_2)[/latex] be [latex](6, 5)[/latex].
Now:
[latex]\Delta x^2 = (x_2 - x_1)^2[/latex] or [latex][6 - (-6)]^2[/latex] and [latex]\Delta y^2 = (y_2 - y_1)^2[/latex] or [latex][5 - (-4)]^2[/latex].
This means that
[latex]d^2 = [6 - (-6)]^2 + [5 - (-4)]^2[/latex]
or
[latex]d^2 = [12]^2 + [9]^2[/latex]
which reduces to
[latex]d^2 = 144 + 81[/latex]
or
[latex]d^2 = 225[/latex]
Taking the square root, the result is [latex]d = 15[/latex].
Finding the Midway Between Two Points (Midpoint)
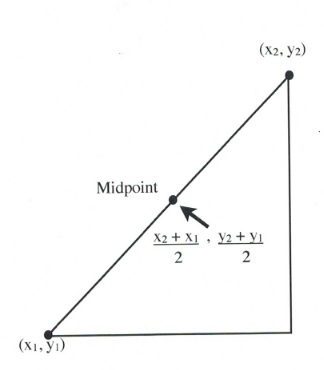
The logic used to find the midpoint between two data points [latex](x_1, y_1)[/latex] and [latex](x_2, y_2)[/latex] on a graph involves finding the average values of the [latex]x[/latex] data points [latex](x_1, x_2)[/latex] and the of the [latex]y[/latex] data points [latex](y_1, y_2)[/latex]. The averages are found by adding both data points together and dividing them by [latex]2[/latex].
In an equation, this looks like:
[latex]x_{\text{mid}}=\dfrac{x_2+x_1}{2}[/latex] and [latex]y_{\text{mid}}=\dfrac{y_2+y_1}{2}[/latex]
Example 3.2.2
Find the midpoint between the points [latex](-2, 3)[/latex] and [latex](6, 9)[/latex].
We start by adding the two [latex]x[/latex] data points [latex](x_1 + x_2)[/latex] and then dividing this result by 2.
[latex]x_{\text{mid}} = \dfrac{(-2 + 6)}{2}[/latex]
or
[latex]\dfrac{4}{2} = 2[/latex]
The midpoint’s [latex]y[/latex]-coordinate is found by adding the two [latex]y[/latex] data points [latex](y_1 + y_2)[/latex] and then dividing this result by 2.
[latex]y_{\text{mid}} = \dfrac{(9 + 3)}{2}[/latex]
or
[latex]\dfrac{12}{2} = 6[/latex]
The midpoint between the points [latex](-2, 3)[/latex] and [latex](6, 9)[/latex] is at the data point [latex](2, 6)[/latex].
Questions
For questions 1 to 8, find the distance between the points.
- (−6, −1) and (6, 4)
- (1, −4) and (5, −1)
- (−5, −1) and (3, 5)
- (6, −4) and (12, 4)
- (−8, −2) and (4, 3)
- (3, −2) and (7, 1)
- (−10, −6) and (−2, 0)
- (8, −2) and (14, 6)
For questions 9 to 16, find the midpoint between the points.
- (−6, −1) and (6, 5)
- (1, −4) and (5, −2)
- (−5, −1) and (3, 5)
- (6, −4) and (12, 4)
- (−8, −1) and (6, 7)
- (1, −6) and (3, −2)
- (−7, −1) and (3, 9)
- (2, −2) and (12, 4)

