Chapter 4: Inequalities
4.5 Geometric Word Problems
It is common to run into geometry-based word problems that look at either the interior angles, perimeter, or area of shapes. When looking at interior angles, the sum of the angles of any polygon can be found by taking the number of sides, subtracting 2, and then multiplying the result by 180°. In other words:
[latex]\text{sum of interior angles} = 180^{\circ} \times (\text{number of sides} - 2)[/latex]
This means the interior angles of a triangle add up to 180° × (3 − 2), or 180°. Any four-sided polygon will have interior angles adding to 180° × (4 − 2), or 360°. A chart can be made of these:
[latex]\begin{array}{rrrrrr} \text{3 sides:}&180^{\circ}&\times&(3-2)&=&180^{\circ} \\ \text{4 sides:}&180^{\circ}&\times&(4-2)&=&360^{\circ} \\ \text{5 sides:}&180^{\circ}&\times&(5-2)&=&540^{\circ} \\ \text{6 sides:}&180^{\circ}&\times&(6-2)&=&720^{\circ} \\ \text{7 sides:}&180^{\circ}&\times&(7-2)&=&900^{\circ} \\ \text{8 sides:}&180^{\circ}&\times&(8-2)&=&1080^{\circ} \\ \end{array}[/latex]
Example 4.5.1
The second angle [latex](A_2)[/latex] of a triangle is double the first [latex](A_1).[/latex] The third angle [latex](A_3)[/latex] is 40° less than the first [latex](A_1).[/latex] Find the three angles.
The relationships described in equation form are as follows:
[latex]A_2 = 2A_1 \text{ and } A_3 = A_1 - 40^{\circ}[/latex]
Because the shape in question is a triangle, the interior angles add up to 180°. Therefore:
[latex]A_1 + A_2 + A_3 = 180^{\circ}[/latex]
Which can be simplified using substitutions:
[latex]A_1 + (2A_1) + (A_1 - 40^{\circ}) = 180^{\circ}[/latex]
Which leaves:
[latex]\begin{array}{rrrrrrrrrrr} 2A_1&+&A_1&+&A_1&-&40^{\circ}&=&180^{\circ}&&&\\ &&&&4A_1&-&40^{\circ}&=&180^{\circ}&&\\ \\ &&&&&&4A_1&=&180^{\circ}&+&40^{\circ}\\ \\ &&&&&&A_1&=&\dfrac{220^{\circ}}{4}&\text{or}&55^{\circ} \end{array}[/latex]
This means [latex]A_2 = 2 (55^{\circ})[/latex] or 110° and [latex]A_3 = 55^{\circ}-40^{\circ}[/latex] or 15°.
| Shape | Picture | Area | Perimeter |
|---|---|---|---|
| Circle | 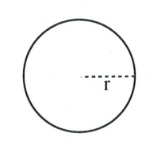 |
[latex]\pi r^2[/latex] | [latex]2\pi r[/latex] |
| Square | 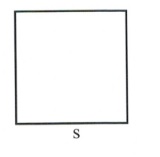 |
[latex]s^2[/latex] | [latex]4s[/latex] |
| Rectangle | 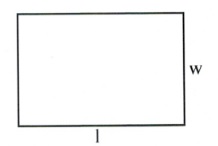 |
[latex]lw[/latex] | [latex]2l+2w[/latex] |
| Triangle | 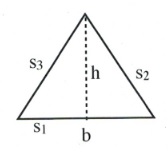 |
[latex]\dfrac{1}{2}bh[/latex] | [latex]s_1+s_2+s_3[/latex] |
| Rhombus | 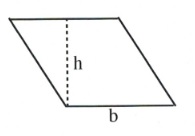 |
[latex]bh[/latex] | [latex]4b[/latex] |
| Trapezoid | 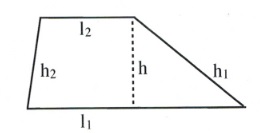 |
[latex]\dfrac{1}{2}\left(l_1+l_2\right)h[/latex] | [latex]l_1+l_2+h_1+h_2[/latex] |
| Parallelogram | 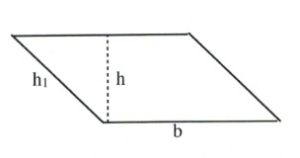 |
[latex]bh[/latex] | [latex]2h_1+2b[/latex] |
| Regular polygon ([latex]n[/latex]-gon) | 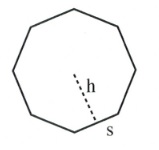 |
[latex]\left(\dfrac{1}{2}sh\right)(\text{number of sides})[/latex] | [latex]s(\text{number of sides})[/latex] |
Another common geometry word problem involves perimeter, or the distance around an object. For example, consider a rectangle, for which [latex]\text{perimeter} = 2l + 2w.[/latex]
Example 4.5.2
If the length of a rectangle is 5 m less than twice the width, and the perimeter is 44 m long, find its length and width.
The relationships described in equation form are as follows:
[latex]L = 2W - 5 \text{ and } P = 44[/latex]
For a rectangle, the perimeter is defined by:
[latex]P = 2 W + 2 L[/latex]
Substituting for [latex]L[/latex] and the value for the perimeter yields:
[latex]44 = 2W + 2 (2W - 5)[/latex]
Which simplifies to:
[latex]44 = 2W + 4W - 10[/latex]
Further simplify to find the length and width:
[latex]\begin{array}{rrrrlrrrr} 44&+&10&=&6W&&&& \\ \\ &&54&=&6W&&&& \\ \\ &&W&=&\dfrac{54}{6}&\text{or}&9&& \\ \\ &\text{So}&L&=&2(9)&-&5&\text{or}&13 \\ \end{array}[/latex]
The width is 9 m and the length is 13 m.
Other common geometric problems are:
Example 4.5.3
A 15 m cable is cut into two pieces such that the first piece is four times larger than the second. Find the length of each piece.
The relationships described in equation form are as follows:
[latex]P_1 + P_2 = 15 \text{ and } P_1 = 4P_2[/latex]
Combining these yields:
[latex]\begin{array}{rrrrrrr} 4P_2&+&P_2&=&15&& \\ \\ &&5P_2&=&15&& \\ \\ &&P_2&=&\dfrac{15}{5}&\text{or}&3 \end{array}[/latex]
This means that [latex]P_2 =[/latex] 3 m and [latex]P_1 = 4 (3),[/latex] or 12 m.
Questions
For questions 1 to 8, write the formula defining each relation. Do not solve.
- The length of a rectangle is 3 cm less than double the width, and the perimeter is 54 cm.
- The length of a rectangle is 8 cm less than double its width, and the perimeter is 64 cm.
- The length of a rectangle is 4 cm more than double its width, and the perimeter is 32 cm.
- The first angle of a triangle is twice as large as the second and 10° larger than the third.
- The first angle of a triangle is half as large as the second and 20° larger than the third.
- The sum of the first and second angles of a triangle is half the amount of the third angle.
- A 140 cm cable is cut into two pieces. The first piece is five times as long as the second.
- A 48 m piece of hose is to be cut into two pieces such that the second piece is 5 m longer than the first.
For questions 9 to 18, write and solve the equation describing each relationship.
- The second angle of a triangle is the same size as the first angle. The third angle is 12° larger than the first angle. How large are the angles?
- Two angles of a triangle are the same size. The third angle is 12° smaller than the first angle. Find the measure of the angles.
- Two angles of a triangle are the same size. The third angle is three times as large as the first. How large are the angles?
- The second angle of a triangle is twice as large as the first. The measure of the third angle is 20° greater than the first. How large are the angles?
- Find the dimensions of a rectangle if the perimeter is 150 cm and the length is 15 cm greater than the width.
- If the perimeter of a rectangle is 304 cm and the length is 40 cm longer than the width, find the length and width.
- Find the length and width of a rectangular garden if the perimeter is 152 m and the width is 22 m less than the length.
- If the perimeter of a rectangle is 280 m and the width is 26 m less than the length, find its length and width.
- A lab technician cuts a 12 cm piece of tubing into two pieces such that one piece is two times longer than the other. How long are the pieces?
- An electrician cuts a 30 m piece of cable into two pieces. One piece is 2 m longer than the other. How long are the pieces?

