Chapter 5: Systems of Equations
5.4 Solving for Three Variables
When given three variables, you are given the equation for a plane or a flat surface similar to a sheet of paper. Some of the possible solutions to the intersections of these equations can be visualized below.
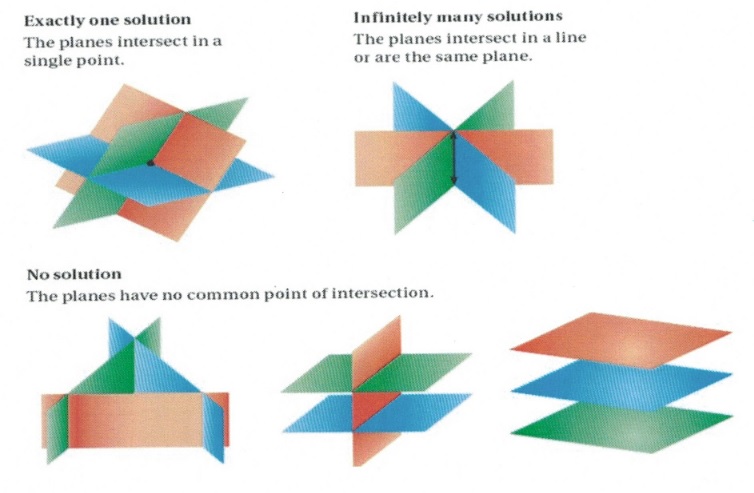
In solving systems of equations with three variables, use the strategies that are used to solve systems of two equations. One recommended method is to eliminate one variable at the onset, thus turning the set of three equations with three unknowns into two equations with two unknowns. The standard method to work with three equations or more is to use subtraction and/or addition.
Example 5.4.1
Find the intersection or the solution to the following system of equations: [latex]3x+2y-z=-1, -2x-2y+3z=5,[/latex] and [latex]5x+2y-z=3.[/latex]
As we did with a set of two equations, first line up the equations to choose the variable that we wish to eliminate:
[latex]\left\{ \begin{array}{rrrrrrr} 3x&+&2y&-&z&=&-1 \\ -2x&-&2y&+&3z&=&5 \\ 5x&+&2y&-&z&=&3 \end{array} \right.[/latex]
For these equations, it looks easiest to eliminate the [latex]y[/latex]-variable. To do this, add the first and second equations together and then add the second and third equations together:
[latex]\begin{array}{rr} \begin{array}{rrrrrrrr} &3x&+&2y&-&z&=&-1 \\ +&-2x&-&2y&+&3z&=&5 \\ \hline &&&x&+&2z&=&4 \end{array} &\hspace{0.25in} \begin{array}{rrrrrrrr} &-2x&-&2y&+&3z&=&5 \\ +&5x&+&2y&-&z&=&3 \\ \hline &&&3x&+&2z&=&8 \end{array} \end{array}[/latex]
Now, you are left with [latex]x+2z=4[/latex] and [latex]3x + 2z = 8.[/latex] We now solve these as done previously with a set of two equations:
[latex]\left\{ \begin{array}{rrrrr} x&+&2z&=&4 \\ 3x&+&2z&=&8 \end{array}\right.[/latex]
Multiply either the top or the bottom equation by −1 to eliminate the [latex]z[/latex]-variable.
[latex]\begin{array}{rrrrrrr} &(x&+&2z&=&4)&(-1) \\ &3x&+&2z&=&8& \\ \\ &-x&-&2z&=&-4& \\ +&3x&+&2z&=&8& \\ \hline &&&\dfrac{2x}{2}&=&\dfrac{4}{2}& \\ \\ &&&x&=&2& \end{array}[/latex]
Next, find [latex]z[/latex] using one of [latex]x+2z=4[/latex] or [latex]3x+2z=8[/latex] and the solution [latex]x= 2.[/latex] [latex]x+2z=4[/latex] looks to be the easiest to work with.
[latex]\begin{array}{rrrrr} x&+&2z&=&4 \\ 2&+&2z&=&4 \\ -2&&&&-2 \\ \hline &&\dfrac{2z}{2}&=&\dfrac{2}{2} \\ \\ &&z&=&1 \end{array}[/latex]
Finally, find [latex]y[/latex] using one of the original three equations:
[latex]\begin{array}{rrrrrrr} 3x&+&2y&-&z&=&-1 \\ 3(2)&+&2y&-&(1)&=&-1 \\ 6&+&2y&-&1&=&-1 \\ &&5&+&2y&=&-1 \\ &&-5&&&=&-5 \\ \hline &&&&\dfrac{2y}{2}&=&\dfrac{-6}{2} \\ \\ &&&&y&=&-3 \end{array}[/latex]
These planes intersect at the point [latex]x = 2,[/latex] [latex]y = -3,[/latex] and [latex]z = 1[/latex], or the coordinate [latex](2, -3, 1).[/latex]
Sometimes, you are given a set of three equations with missing variables. These systems of equations require slightly more thought to solve than the previous problems.
Example 5.4.2
Find the intersection or the solution to the following system of equations: [latex]x+2y-z=0, 3x-2y=-2,[/latex] and [latex]y+z=3.[/latex]
First, line up the equations to choose the variable that we wish to eliminate:
[latex]\left\{ \begin{array}{rrrrrrr} x&+&2y&-&z&=&0 \\ 3x&-&2y&&&=&-2 \\ &&y&+&z&=&3 \end{array}\right.[/latex]
In this example, adding the first and last equations eliminates the variable [latex]z,[/latex] without having to modify any of the equations:
[latex]\begin{array}{rrrrrrrr} &x&+&2y&-&z&=&0 \\ +&&&y&+&z&=&3 \\ \hline &&&x&+&3y&=&3 \\ \end{array}[/latex]
Now, there are two equations left:
[latex]\left\{ \begin{array}{rrrrr} 3x&-&2y&=&-2 \\ x&+&3y&=&3 \end{array}\right.[/latex]
First multiply the bottom equation by −3, then add it to the top equation, to eliminate the variable [latex]x[/latex]:
[latex]\begin{array}{rrrrrrr} &(x&+&3y&=&3)&(-3) \\ \\ &3x&-&2y&=&-2& \\ +&-3x&-&9y&=&-9& \\ \hline &&&-11y&=&-11& \\ &&&y&=&1& \\ \end{array}[/latex]
Now choose one of the two remaining equations, [latex]3x-2y=-2[/latex] or [latex]x+3y=3,[/latex] to find the variable [latex]x.[/latex] Choosing [latex]x+3y= 3,[/latex] leaves:
[latex]\begin{array}{rrrrr} x&+&3(1)&=&3 \\ x&+&3&=&3 \\ &-&3&=&-3 \\ \hline &&x&=&0 \end{array}[/latex]
Finally, to find the third variable, use one of the original three equations: [latex]x+2y-z=0, 3x-2y=-2,[/latex] or [latex]y+z=3.[/latex] Choosing [latex]y + z = 3,[/latex] gives:
[latex]\begin{array}{rrrrr} (1)&+&z&=&3 \\ &&z&=&2 \end{array}[/latex]
These planes intersect at the point [latex]x = 0, y = 1,[/latex] and [latex]z = 2,[/latex] or the coordinate [latex](0, 1, 2).[/latex]
Questions
Solve each of the following systems of equations.
- [latex]\left\{ \begin{array}{rrrrrrr} a&-&b&+&2c&=&2 \\ 2a&+&b&-&c&=&2 \\ a&+&b&+&c&=&3 \end{array}\right.[/latex]
- [latex]\left\{ \begin{array}{rrrrrrr} 2a&+&3b&-&c&=&12 \\ 3a&+&4b&+&c&=&19 \\ a&-&2b&+&c&=&-3 \end{array}\right.[/latex]
- [latex]\left\{ \begin{array}{rrrrrrr} 3x&+&y&-&z&=&7 \\ x&+&3y&-&z&=&5 \\ x&+&y&+&2z&=&3 \end{array}\right.[/latex]
- [latex]\left\{ \begin{array}{rrrrrrr} x&+&y&+&z&=&4 \\ x&+&2y&+&3z&=&10 \\ x&-&y&+&4z&=&20 \end{array}\right.[/latex]
- [latex]\left\{ \begin{array}{rrrrrrr} x&+&2y&-&z&=&0 \\ 2x&-&y&+&z&=&15 \\ 3x&-&2y&-&4z&=&-5 \end{array}\right.[/latex]
- [latex]\left\{ \begin{array}{rrrrrrr} x&-&y&+&2z&=&-3 \\ x&+&2y&+&3z&=&4 \\ 2x&+&y&+&z&=&-3 \end{array}\right.[/latex]
- [latex]\left\{ \begin{array}{rrrrrrr} x&+&y&+&z&=&6 \\ 2x&-&y&-&z&=&-3 \\ x&-&2y&+&3z&=&6 \end{array}\right.[/latex]
- [latex]\text{tricky:} \left\{ \begin{array}{rrrrrrr} x&+&y&-&z&=&0 \\ x&+&2y&-&4z&=&0 \\ 2x&+&y&+&z&=&0 \end{array}\right.[/latex]
- [latex]\left\{ \begin{array}{rrrrrrr} x&+&y&+&z&=&2 \\ 2x&-&y&+&3z&=&9 \\ &&y&-&z&=&-3 \end{array}\right.[/latex]
- [latex]\left\{ \begin{array}{rrrrrrr} 6x&-&y&-&2z&=&-1 \\ 4x&&&+&z&=&3 \\ -2x&+&3y&&&=&5 \end{array}\right.[/latex]
- [latex]\left\{ \begin{array}{rrrrrrr} &&y&+&z&=&5 \\ 2x&-&3y&+&z&=&-1 \\ x&&&-&z&=&-2 \end{array}\right.[/latex]
- [latex]\left\{ \begin{array}{rrrrrrr} 3x&+&4y&-&z&=&11 \\ &&y&+&2z&=&-4 \\ -2x&+&y&&&=&-6 \end{array}\right.[/latex]
- [latex]\left\{ \begin{array}{rrrrrrr} x&+&6y&+&3z&=&30 \\ 2x&&&+&2z&=&4 \\ &&-2y&+&z&=&-6 \end{array}\right.[/latex]
- [latex]\left\{ \begin{array}{rrrrrrr} x&-&y&+&2z&=&0 \\ x&+&2y&&&=&1 \\ 2x&&&+&z&=&4 \end{array}\right.[/latex]
- [latex]\left\{ \begin{array}{rrrrrrr} x&+&y&+&z&=&4 \\ &&-y&-&z&=&-4 \\ x&-&2y&&&=&0 \end{array}\right.[/latex]
- [latex]\left\{ \begin{array}{rrrrrrr} x&+&y&-&z&=&2 \\ &&2y&-&4z&=&-4 \\ 2x&&&+&z&=&6 \end{array}\right.[/latex]

