Chapter 6: Polynomials
6.7 Dividing Polynomials
Dividing polynomials is a process very similar to long division of whole numbers. But before looking at that, first master dividing a polynomial by a monomial. The way to do this is very similar to distributing, but the operation to distribute is the division, dividing each term by the monomial and reducing the resulting expression. This is shown in the following examples.
Example 6.7.1
Divide the following:
- [latex](9x^5 + 6x^4 - 18x^3 - 24x^2)\div 3x^2[/latex]Breaking this up into fractions, we get:[latex]\dfrac{9x^5}{3x^2}+ \dfrac{6x^4}{3x^2}- \dfrac{18x^3}{3x^2}- \dfrac{24x^2}{3x^2}[/latex]Which yields:[latex]3x^3+2x^2-6x-8[/latex]
- [latex](8x^3 + 4x^2 - 2x + 6)\div 4x^2[/latex]Breaking this up into fractions, we get:[latex]\dfrac{8x^3}{4x^2}+ \dfrac{4x^2}{4x^2} -\dfrac{2x}{4x^2} +\dfrac{6}{4x^2}[/latex]Which yields:[latex]2x+1-\dfrac{1}{2x}+\dfrac{3}{2x^2}[/latex]
Long division is required when dividing by more than just a monomial. Long division with polynomials is similar to long division with whole numbers.
Example 6.7.2
Divide the polynomial [latex]3x^3 - 5x^2 - 32x + 7[/latex] by [latex]x - 4.[/latex]
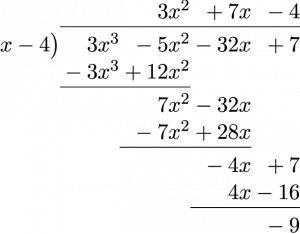
The steps to get this result are as follows:
- Divide [latex]3x^3[/latex] by [latex]x,[/latex] yielding [latex]3x^2.[/latex] Multiply [latex](x-4)[/latex] by [latex]3x^2[/latex], yielding [latex]3x^3+12x^2.[/latex] Subtract and bring down the next term and repeat.
- Divide [latex]7x^2[/latex] by [latex]x,[/latex] yielding [latex]7x.[/latex] Multiply [latex](x-4)[/latex] by [latex]7x,[/latex] yielding [latex]7x^2-28x.[/latex] Subtract and bring down the next term and repeat.
- Divide [latex]-4x[/latex] by [latex]x,[/latex] yielding [latex]-4[/latex]. Multiply [latex](x-4)[/latex] by [latex]-4,[/latex] yielding [latex]-4x+16.[/latex] Subtract.
The solution can be written as either [latex]3x^2+7x-4 \text{ R }-9[/latex] or [latex]3x^2+7x-4-\dfrac{9}{x-4}.[/latex]
The more formal way of writing this answer is the second option.
Example 6.7.3
Divide the polynomial [latex]6x^3 - 8x^2 + 10x + 100[/latex] by [latex]2x + 4.[/latex]
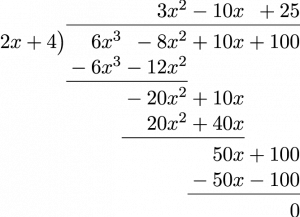
The steps to get this result are as follows:
- Divide [latex]6x^3[/latex] by [latex]2x,[/latex] yielding [latex]3x^2.[/latex] Multiply [latex](2x+4)[/latex] by [latex]3x^2,[/latex] yielding [latex]6x^3+12x^2.[/latex] Subtract and bring down the next term and repeat.
- Divide [latex]-20x^2[/latex] by [latex]2x,[/latex] yielding [latex]-10x.[/latex] Multiply [latex](2x+4)[/latex] by [latex]-10x,[/latex] yielding [latex]-20x^2-40x.[/latex] Subtract and bring down the next term and repeat.
- Divide [latex]50x[/latex] by [latex]2x,[/latex] yielding 25. Multiply [latex](2x+4)[/latex] by 25, yielding [latex]50x+100.[/latex] Subtract.
The solution is [latex]3x^2 - 10x + 25[/latex] with no remainder.
Questions
Solve the following polynomial divisions.
- [latex](20x^4 + x^3 + 2x^2)\div (4x^3)[/latex]
- [latex](5x^4 + 45x^3 + 4x^2) \div (9x)[/latex]
- [latex](20n^4 + n^3 + 40n^2) \div (10n)[/latex]
- [latex](3k^3 + 4k^2 + 2k) \div (8k)[/latex]
- [latex](12x^4 + 24x^3 + 3x^2) \div (6x)[/latex]
- [latex](5p^4 + 16p^3 + 16p^2) \div (4p)[/latex]
- [latex](10n^4 + 50n^3 + 2n^2) \div (10n^2)[/latex]
- [latex](3m^4 + 18m^3 + 27m^2) \div (9m^2)[/latex]
- [latex](45x^2 + 56x + 16) \div (9x + 4)[/latex]
- [latex](6x^2 + 16x + 16) \div (6x - 2)[/latex]
- [latex](10x^2 - 32x + 6) \div (10x - 2)[/latex]
- [latex](x^2 + 7x + 12) \div (x + 4)[/latex]
- [latex](4x^2 - 33x + 35) \div (4x - 5)[/latex]
- [latex](4x^2 - 23x - 35) \div (4x + 5)[/latex]
- [latex](x^3 + 15x^2 + 49x - 49) \div (x + 7)[/latex]
- [latex](6x^3 - 12x^2 - 43x - 20) \div (x - 4)[/latex]
- [latex](x^3 - 6x - 40) \div (x + 4)[/latex]
- [latex](x^3 - 16x^2 + 512) \div (x - 8)[/latex]
- [latex](x^3 - x^2 - 8x - 16) \div (x - 4)[/latex]
- [latex](2x^3 + 6x^2 + 4x + 12) \div (2x + 6)[/latex]
- [latex](12x^3 + 12x^2 - 15x - 9) \div (2x + 3)[/latex]
- [latex](6x + 18 - 21x^2 + 4x^3) \div (4x + 3)[/latex]

