Chapter 6: Polynomials
6.9 Pascal’s Triangle and Binomial Expansion
Pascal’s triangle (1653) has been found in the works of mathematicians dating back before the 2nd century BC. While Pascal’s triangle is useful in many different mathematical settings, it will be applied to the expansion of binomials. In this application, Pascal’s triangle will generate the leading coefficient of each term of a binomial expansion in the form of:
[latex](a+b)^n[/latex]
For example:
[latex]\begin{array}{llllllllllllllll} (a&+&b)^2&=&a^2&+&2ab&+&b^2\hspace{0.25in}&(1&+&2&+&1)&& \\ (a&+&b)^3&=&a^3&+&3a^2b&+&b^3\hspace{0.25in}&(1&+&3&+&3&+&1) \end{array}[/latex]
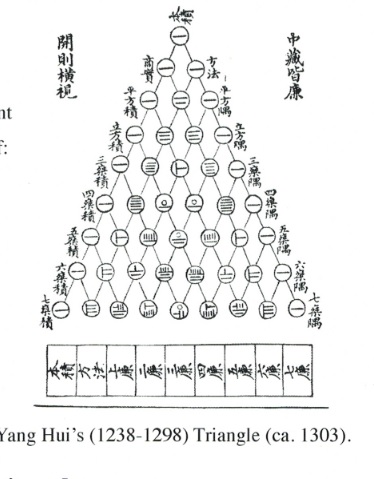
Pascal’s Triangle
[latex]\begin{array}{lclcl} (a+b)^0&1&2^0&1&(a-b)^0 \\ (a+b)^1&1+1&2^1&1-1&(a-b)^1 \\ (a+b)^2&1+2+1&2^2&1-2+1&(a-b)^2 \\ (a+b)^3&1+3+3+1&2^3&1-3+3-1&(a-b)^3 \\ (a+b)^4&1+4+6+4+1&2^4&1-4+6-4+1&(a-b)^4 \\ (a+b)^5&1+5+10+10+5+1&2^5&1-5+10-10+5-1&(a-b)^5 \\ (a+b)^6&1+6+15+20+15+6+1&2^6&1-6+15-20+15-6+1&(a-b)^6 \\ (a+b)^7&1+7+21+35+35+21+7+1&2^7&1-7+21-35+35-21+7-1&(a-b)^7 \end{array}[/latex]
The generation of each row of Pascal’s triangle is done by adding the two numbers above it.
[latex]\begin{array}{cl} 1&\text{Start with 1} \\ 1+1&\text{The outside number is always 1} \\ 1+2+1&\text{The two 1's in the last row add to 2} \\ 1+3+3+1&1+2 \text{ above adds to 3} \\ 1+4+6+4+1& \\ 1+5+10+10+5+1& \\ 1+6+15+20+15+6+1& \\ 1+7+21+35+35+21+7+1 & \text{We can extend Pascal's triangle using this} \\ 1+8+28+56+70+56+28+8+1&(a+b)^8 \\ 1+9+36+84+126+126+84+36+9+1&(a+b)^9 \\ \end{array}[/latex]
Example 6.9.1
Use Pascal’s triangle to expand [latex](a + b)^9.[/latex]
The variables will follow a pattern of rising and falling powers:
[latex]a^9 + a^8b + a^7b^2 + a^6b^3 + a^5b^4 + a^4b^5 + a^3b^6 + a^2b^7 + ab^8 + b^9[/latex]
When we insert the coefficients found from Pascal’s triangle, we create:
[latex]a^9 + 9a^8b + 36a^7b^2 + 84a^6b^3 + 126a^5b^4 + 126a^4b^5 + 84a^3b^6 + 36a^2b^7 + 8ab^8 + b^9[/latex]
Problem: Use Pascal’s triangle to expand the binomial [latex](a + b)^{12}.[/latex]
A Visual Representation of Binomial Expansion
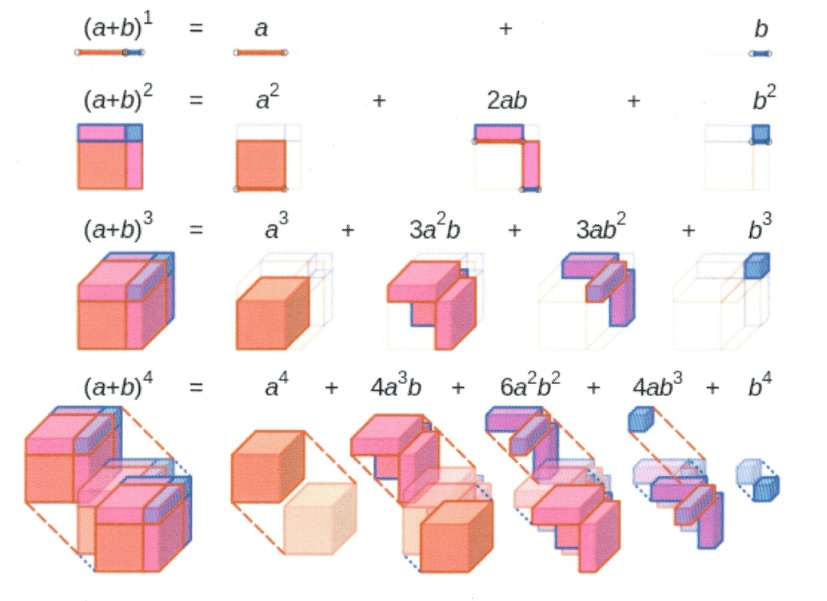
The fourth expansion of the binomial is generally held to represent time, with the first three expansions being width, length, and height. While we live in a four-dimensional universe (string theory suggests ten dimensions), efforts to represent the fourth dimension of time are challenging. Carl Sagan describes the fourth dimension using an analogy created by Edwin Abbot (Abbot: Flatland: A Romance of Many Dimensions). A video clip of Sagan’s “Tesseract, 4th Dimension Made Easy” can be found on YouTube.
