CHAPTER 1 Whole Numbers, Integers, and Introduction to Algebra
1.3 Evaluate, Simplify, and Translate Expressions
Learning Objectives
By the end of this section, you will be able to:
- Evaluate algebraic expressions
- Identify terms, coefficients, and like terms
- Simplify expressions by combining like terms
- Translate word phrases to algebraic expressions
Evaluate Algebraic Expressions
In the last section, we simplified expressions using the order of operations. In this section, we’ll evaluate expressions—again following the order of operations.
To evaluate an algebraic expression means to find the value of the expression when the variable is replaced by a given number. To evaluate an expression, we substitute the given number for the variable in the expression and then simplify the expression using the order of operations.
EXAMPLE 1
Evaluate ![]() when
when
a. To evaluate, substitute ![]() for
for ![]() in the expression, and then simplify.
in the expression, and then simplify.
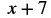 |
|
| Substitute. | 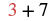 |
| Add. | 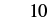 |
When ![]() , the expression
, the expression ![]() has a value of
has a value of ![]() .
.
b. To evaluate, substitute ![]() for
for ![]() in the expression, and then simplify.
in the expression, and then simplify.
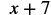 |
|
| Substitute. | 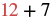 |
| Add. | 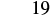 |
When ![]() , the expression
, the expression ![]() has a value of
has a value of ![]() .
.
Notice that we got different results for parts a) and b) even though we started with the same expression. This is because the values used for ![]() were different. When we evaluate an expression, the value varies depending on the value used for the variable.
were different. When we evaluate an expression, the value varies depending on the value used for the variable.
TRY IT 1.1
Evaluate:
![]()
Show Answer
- 10
- 19
TRY IT 1.2
Evaluate:
![]()
Show Answer
- 4
- 12
EXAMPLE 2
Evaluate ![]()
Remember ![]() means
means ![]() times
times ![]() , so
, so ![]() means
means ![]() times
times ![]() .
.
a. To evaluate the expression when ![]() , we substitute
, we substitute ![]() for
for ![]() , and then simplify.
, and then simplify.
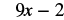 |
|
 |
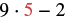 |
| Multiply. | 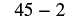 |
| Subtract. |  |
b. To evaluate the expression when ![]() , we substitute
, we substitute ![]() for
for ![]() , and then simplify.
, and then simplify.
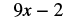 |
|
 |
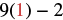 |
| Multiply. | 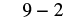 |
| Subtract. |  |
Notice that in part a) that we wrote ![]() and in part b) we wrote
and in part b) we wrote ![]() . Both the dot and the parentheses tell us to multiply.
. Both the dot and the parentheses tell us to multiply.
TRY IT 2.1
Evaluate:
![]()
Show Answer
- 13
- 5
TRY IT 2.2
Evaluate:
![]()
Show Answer
- 8
- 16
EXAMPLE 3
Evaluate ![]() when
when ![]() .
.
We substitute ![]() for
for ![]() , and then simplify the expression.
, and then simplify the expression.
 |
|
 |
 |
| Use the definition of exponent. | 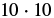 |
| Multiply. | 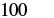 |
When ![]() , the expression
, the expression ![]() has a value of
has a value of ![]() .
.
TRY IT 3.1
Evaluate:
![]() .
.
Show Answer
64
TRY IT 3.2
Evaluate:
![]() .
.
Show Answer
216
EXAMPLE 4
![]() .
.
In this expression, the variable is an exponent.
 |
|
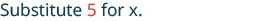 |
 |
| Use the definition of exponent. | 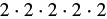 |
| Multiply. |  |
When ![]() , the expression
, the expression ![]() has a value of
has a value of ![]() .
.
TRY IT 4.1
Evaluate:
![]() .
.
Show Answer
64
TRY IT 4.2
Evaluate:
![]() .
.
Show Answer
81
EXAMPLE 5
![]() .
.
This expression contains two variables, so we must make two substitutions.
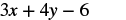 |
|
 |
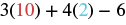 |
| Multiply. | 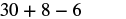 |
| Add and subtract left to right. |  |
When ![]() and
and ![]() , the expression
, the expression ![]() has a value of
has a value of ![]() .
.
TRY IT 5.1
Evaluate:
![]()
Show Answer
33
TRY IT 5.2
Evaluate:
![]()
Show Answer
10
EXAMPLE 6
![]() .
.
We need to be careful when an expression has a variable with an exponent. In this expression, ![]() means
means ![]() and is different from the expression
and is different from the expression ![]() , which means
, which means ![]() .
.
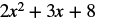 |
|
 |
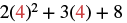 |
| Simplify |
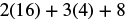 |
| Multiply. | 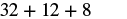 |
| Add. |  |
TRY IT 6.1
Evaluate:
![]() .
.
Show Answer
40
TRY IT 6.2
Evaluate:
![]() .
.
Show Answer
9
Identify Terms, Coefficients, and Like Terms
Algebraic expressions are made up of terms. A term is a constant or the product of a constant and one or more variables. Some examples of terms are ![]() .
.
The constant that multiplies the variable(s) in a term is called the coefficient. We can think of the coefficient as the number in front of the variable. The coefficient of the term ![]() is
is ![]() . When we write
. When we write ![]() , the coefficient is
, the coefficient is ![]() , since
, since ![]() . The table below gives the coefficients for each of the terms in the left column.
. The table below gives the coefficients for each of the terms in the left column.
| Term | Coefficient |
|---|---|
An algebraic expression may consist of one or more terms added or subtracted. In this chapter, we will only work with terms that are added together. The table below gives some examples of algebraic expressions with various numbers of terms. Notice that we include the operation before a term with it.
| Expression | Terms |
|---|---|
EXAMPLE 7
Identify each term in the expression ![]() . Then identify the coefficient of each term.
. Then identify the coefficient of each term.
The expression has four terms. They are ![]() , and
, and ![]() .
.
The coefficient of ![]() is
is ![]() .
.
The coefficient of ![]() is
is ![]() .
.
Remember that if no number is written before a variable, the coefficient is ![]() . So the coefficient of
. So the coefficient of ![]() is
is ![]() .
.
The coefficient of a constant is the constant, so the coefficient of ![]() is
is ![]() .
.
TRY IT 7.1
Identify all terms in the given expression, and their coefficients:
![]()
Show Answer
The terms are 4x, 3b, and 2. The coefficients are 4, 3, and 2
TRY IT 7.2
Identify all terms in the given expression, and their coefficients:
![]()
Show Answer
The terms are 9a, 13a2, and a3, The coefficients are 9, 13, and 1
Some terms share common traits. Look at the following terms. Which ones seem to have traits in common?
![]()
Which of these terms are like terms?
- The terms
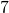 and
and 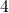 are both constant terms.
are both constant terms. - The terms
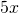 and
and 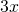 are both terms with
are both terms with 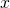 .
. - The terms
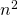 and
and 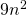 both have
both have 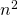 .
.
Terms are called like terms if they have the same variables and exponents. All constant terms are also like terms. So among the terms ![]() ,
,
Like Terms
Terms that are either constants or have the same variables with the same exponents are like terms.
EXAMPLE 8
Identify the like terms:
a. ![]()
Look at the variables and exponents. The expression contains ![]() , and constants.
, and constants.
The terms ![]() and
and ![]() are like terms because they both have
are like terms because they both have ![]() .
.
The terms ![]() and
and ![]() are like terms because they both have
are like terms because they both have ![]() .
.
The terms ![]() and
and ![]() are like terms because they are both constants.
are like terms because they are both constants.
The term ![]() does not have any like terms in this list since no other terms have the variable
does not have any like terms in this list since no other terms have the variable ![]() raised to the power of
raised to the power of ![]() .
.
b. ![]()
Look at the variables and exponents. The expression contains the terms ![]()
The terms ![]() and
and ![]() are like terms because they both have
are like terms because they both have ![]() .
.
The terms ![]() are like terms because they all have
are like terms because they all have ![]() .
.
The term ![]() has no like terms in the given expression because no other terms contain the two variables
has no like terms in the given expression because no other terms contain the two variables ![]() .
.
TRY IT 8.1
Identify the like terms in the list or the expression:
![]()
Show Answer
9, 15; 2x3 and 8x3, y2, and 11y2
TRY IT 8.2
Identify the like terms in the list or the expression:
![]()
Show Answer
4x3 and 6x3; 8x2 and 3x2; 19 and 24
Simplify Expressions by Combining Like Terms
We can simplify an expression by combining the like terms. What do you think ![]() would simplify to? If you thought
would simplify to? If you thought ![]() , you would be right!
, you would be right!
We can see why this works by writing both terms as addition problems.
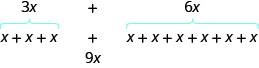
Add the coefficients and keep the same variable. It doesn’t matter what ![]() is. If you have
is. If you have ![]() of something and add
of something and add ![]() more of the same thing, the result is
more of the same thing, the result is ![]() of them. For example,
of them. For example, ![]() oranges plus
oranges plus ![]() oranges is
oranges is ![]() oranges. We will discuss the mathematical properties behind this later.
oranges. We will discuss the mathematical properties behind this later.
The expression ![]() has only two terms. When an expression contains more terms, it may be helpful to rearrange the terms so that like terms are together. The Commutative Property of Addition says that we can change the order of addends without changing the sum. So we could rearrange the following expression before combining like terms.
has only two terms. When an expression contains more terms, it may be helpful to rearrange the terms so that like terms are together. The Commutative Property of Addition says that we can change the order of addends without changing the sum. So we could rearrange the following expression before combining like terms.
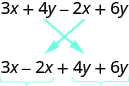
Now it is easier to see the like terms to be combined.
HOW TO: Combine like terms
- Identify like terms.
- Rearrange the expression so like terms are together.
- Add the coefficients of the like terms.
EXAMPLE 9
Simplify the expression: ![]() .
.
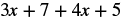 |
|
| Identify the like terms. | 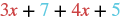 |
| Rearrange the expression, so the like terms are together. | 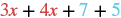 |
| Add the coefficients of the like terms. | 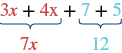 |
| The original expression is simplified to… | 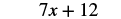 |
TRY IT 9.1
Simplify:
![]()
Show Answer
16x + 17
TRY IT 9.2
Simplify:
![]()
Show Answer
17y + 7
EXAMPLE 10
Simplify the expression: ![]() .
.
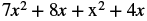 |
|
| Identify the like terms. | 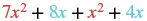 |
| Rearrange the expression so like terms are together. | 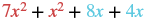 |
| Add the coefficients of the like terms. | 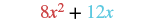 |
These are not like terms and cannot be combined. So ![]() is in simplest form.
is in simplest form.
TRY IT 10.1
Simplify:
![]()
Show Answer
4x2 + 14x
TRY IT 10.2
Simplify:
![]()
Show Answer
12y2 + 15y
Translate Words to Algebraic Expressions
In the previous section, we listed many operation symbols that are used in algebra, and then we translated expressions and equations into word phrases and sentences. Now we’ll reverse the process and translate word phrases into algebraic expressions. The symbols and variables we’ve talked about will help us do that. They are summarized in the table below.
| Operation | Phrase | Expression |
|---|---|---|
| Addition | the sum of the total of |
|
| Subtraction | the difference of |
|
| Multiplication | the product of |
|
| Division | the quotient of the ratio of |
Look closely at these phrases using the four operations:
- the sum of
 and
and 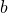
- the difference of
 and
and 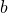
- the product of
 and
and 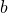
- the quotient of
 and
and 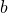
Each phrase tells you to operate on two numbers. Look for the words of and and to find the numbers.
EXAMPLE 11
Translate each word phrase into an algebraic expression:
- the difference of
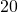 and
and 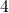
- the quotient of
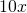 and
and 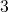
a. The key word is difference, which tells us the operation is subtraction. Look for the words of and and to find the numbers to subtract.
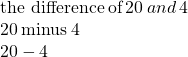
b. The key word is quotient, which tells us the operation is division.
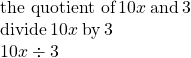
This can also be written as ![]()
TRY IT 11.1
Translate the given word phrase into an algebraic expression:
- the difference of
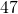 and
and 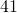
- the quotient of
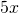 and
and 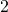
Show Answer
- 47 − 41
- 5x ÷ 2
TRY IT 11.2
Translate the given word phrase into an algebraic expression:
- the sum of
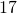 and
and 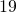
- the product of
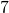 and
and 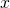
Show Answer
- 17 + 19
- 7x
How old will you be in eight years? What age is eight more years than your age now? Did you add ![]() to your present age? Eight more than means eight added to your present age.
to your present age? Eight more than means eight added to your present age.
How old were you seven years ago? This is seven years less than your age now. You subtract ![]() from your present age. Seven less than means seven subtracted from your present age.
from your present age. Seven less than means seven subtracted from your present age.
EXAMPLE 12
Translate each word phrase into an algebraic expression:
- Eight more than
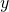
- Seven less than
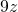
a. The key words are more than. They tell us the operation is addition. More than means “added to”.
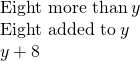
b. The key words are less than. They tell us the operation is subtraction. Less than means “subtracted from”.

TRY IT 12.1
Translate each word phrase into an algebraic expression:
- Eleven more than
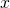
- Fourteen less than
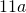
Show Answer
- x + 11
- 11a − 14
TRY IT 12.2
Translate each word phrase into an algebraic expression:
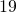 more than
more than 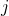
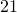 less than
less than 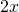
Show Answer
- j + 19
- 2x − 21
EXAMPLE 13
Translate each word phrase into an algebraic expression:
- five times the sum of
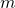 and
and 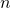
- the sum of five times
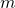 and
and 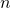
a. There are two operation words: times tells us to multiply and sum tells us to add. Because we are multiplying ![]() times the sum, we need parentheses around the sum of
times the sum, we need parentheses around the sum of ![]() and
and ![]() .
.
five times the sum of ![]() and
and ![]()
![]()
b. To take a sum, we look for the words of and and to see what is being added. Here we are taking the sum of five times ![]() and
and ![]() .
.
the sum of five times ![]() and
and ![]()
![]()
Notice how the use of parentheses changes the result. In part a), we add first and in part b), we multiply first.
TRY IT 13.1
Translate the word phrase into an algebraic expression:
- four times the sum of
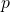 and
and 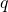
- the sum of four times
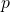 and
and 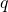
Show Answer
- 4(p + q)
- 4p + q
TRY IT 13.2
Translate the word phrase into an algebraic expression:
- the difference of two times
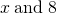
- two times the difference of
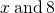
Show Answer
- 2x − 8
- 2(x − 8)
Later in this course, we’ll apply our skills in algebra to solving equations. We’ll usually start by translating a word phrase to an algebraic expression. We’ll need to be clear about what the expression will represent. We’ll see how to do this in the next two examples.
EXAMPLE 14
The height of a rectangular window is ![]() inches less than the width. Let
inches less than the width. Let ![]() represent the width of the window. Write an expression for the height of the window.
represent the width of the window. Write an expression for the height of the window.
| Write a phrase about the height. | |
| Substitute |
|
| Rewrite ‘less than’ as ‘subtracted from’. | |
| Translate the phrase into algebra. |
TRY IT 14.1
The length of a rectangle is ![]() inches less than the width. Let
inches less than the width. Let ![]() represent the width of the rectangle. Write an expression for the length of the rectangle.
represent the width of the rectangle. Write an expression for the length of the rectangle.
Show Answer
w − 5
TRY IT 14.2
The width of a rectangle is ![]() metres greater than the length. Let
metres greater than the length. Let ![]() represent the length of the rectangle. Write an expression for the width of the rectangle.
represent the length of the rectangle. Write an expression for the width of the rectangle.
Show Answer
l + 2
EXAMPLE 15
Blanca has dimes and quarters in her purse. The number of dimes is ![]() less than
less than ![]() times the number of quarters. Let
times the number of quarters. Let ![]() represent the number of quarters. Write an expression for the number of dimes.
represent the number of quarters. Write an expression for the number of dimes.
| Write a phrase about the number of dimes. | two less than five times the number of quarters |
| Substitute |
|
| Translate |
|
| Translate the phrase into algebra. |
TRY IT 15.1
Geoffrey has dimes and quarters in his pocket. The number of dimes is seven less than six times the number of quarters. Let ![]() represent the number of quarters. Write an expression for the number of dimes.
represent the number of quarters. Write an expression for the number of dimes.
Show Answer
6q − 7
TRY IT 15.2
Lauren has dimes and nickels in her purse. The number of dimes is eight more than four times the number of nickels. Let ![]() represent the number of nickels. Write an expression for the number of dimes.
represent the number of nickels. Write an expression for the number of dimes.
Show Answer
4n + 8
Key Concepts
- Combine like terms.
- Identify like terms.
- Rearrange the expression so like terms are together.
- Add the coefficients of the like terms
Glossary
- term
- A term is a constant or the product of a constant and one or more variables.
- coefficient
- The constant that multiplies the variable(s) in a term is called the coefficient.
- like terms
- Terms that are either constants or have the same variables with the same exponents are like terms.
- evaluate
- To evaluate an algebraic expression means to find the value of the expression when the variable is replaced by a given number.
Practice Makes Perfect
Evaluate Algebraic Expressions
In the following exercises, evaluate the expression for the given value.
| 1. |
2. |
| 3. |
4. |
| 5. |
6. |
| 7. |
8. |
| 9. |
10. |
| 11. |
12. |
| 13. |
14. |
| 15. |
16. |
| 17. |
18. |
| 19. |
20. |
Identify Terms, Coefficients, and Like Terms
In the following exercises, list the terms in the given expression.
| 21. |
22. |
| 23. |
24. |
In the following exercises, identify the coefficient of the given term.
| 25. |
26. |
| 27. |
28. |
In the following exercises, identify all sets of like terms.
| 29. |
30. |
| 31. |
32. |
Simplify Expressions by Combining Like Terms
In the following exercises, simplify the given expression by combining like terms.
| 33. |
34. |
| 35. |
36. |
| 37. |
38. |
| 39. |
40. |
| 41. |
42. |
| 43. |
44. |
| 45. |
46. |
| 47. |
48. |
Translate English Phrases into Algebraic Expressions
In the following exercises, translate the given word phrase into an algebraic expression.
| 49. The sum of 8 and 12 | 50. The sum of 9 and 1 |
| 51. The difference of 14 and 9 | 52. 8 less than 19 |
| 53. The product of 9 and 7 | 54. The product of 8 and 7 |
| 55. The quotient of 36 and 9 | 56. The quotient of 42 and 7 |
| 57. The difference of |
58. |
| 59. The product of |
60. The product of |
| 61. The sum of |
62. The sum of |
| 63. The quotient of |
64. The quotient of |
| 65. Eight times the difference of |
66. Seven times the difference of |
| 67. Five times the sum of |
68. times five less than twice |
In the following exercises, write an algebraic expression.
| 69. Adele bought a skirt and a blouse. The skirt cost $15 more than the blouse. Let |
70. Eric has rock and classical CDs in his car. The number of rock CDs is |
| 71. The number of girls in a second-grade class is |
72. Marcella has |
| 73. Greg has nickels and pennies in his pocket. The number of pennies is seven less than twice the number of nickels. Let |
74. Jeannette has $5 and $10 bills in her wallet. The number of fives is three more than six times the number of tens. Let |
Everyday Math
In the following exercises, use algebraic expressions to solve the problem.
| 75. Car insurance Justin’s car insurance has a $750 deductible per incident. This means that he pays $750 and his insurance company will pay all costs beyond $750. If Justin files a claim for $2,100, how much will he pay, and how much will his insurance company pay? | 76. Home insurance Pam and Armando’s home insurance has a $2,500 deductible per incident. This means that they pay $2,500 and their insurance company will pay all costs beyond $2,500. If Pam and Armando file a claim for $19,400, how much will they pay, and how much will their insurance company pay? |
Writing Exercises
| 77. Explain why “the sum of x and y” is the same as “the sum of y and x,” but “the difference of x and y” is not the same as “the difference of y and x.” Try substituting two random numbers for |
78. Explain the difference between |
Answers
| 1. 22 | 3. 26 | 5. 144 |
| 7. 32 | 9. 27 | 11. 21 |
| 13. 41 | 15. 9 | 17. 73 |
| 19. 54 | 21. 15x2, 6x, 2 | 23. 10y3, y, 2 |
| 25. 8 | 27. 5 | 29. x3, 8x3 and 14, 5 |
| 31. 16ab and 4ab; 16b2 and 9b2 | 33. 13x | 35. 26a |
| 37. 7c | 39. 12x + 8 | 41. 10u + 3 |
| 43. 12p + 10 | 45. 22a + 1 | 47. 17x2 + 20x + 16 |
| 49. 8 + 12 | 51. 14 − 9 | 53. 9 ⋅ 7 |
| 55. 36 ÷ 9 | 57. x − 4 | 59. 6y |
| 61. 8x + 3x | 63. |
65. 8 (y − 9) |
| 67. 5 (x + y) | 69. b + 15 | 71. b − 4 |
| 73. 2n − 7 | 75. He will pay $750. His insurance company will pay $1350. | 77. Answers will vary. |
Attributions
This chapter has been adapted from “Evaluate, Simplify, and Translate Expressions” in Prealgebra (OpenStax) by Lynn Marecek, MaryAnne Anthony-Smith, and Andrea Honeycutt Mathis, which is under a CC BY 4.0 Licence. Adapted by Izabela Mazur. See the Copyright page for more information.

