CHAPTER 6 Linear Equations and Graphing
6.7 Chapter Review
Review Exercises
Plot Points in a Rectangular Coordinate System
In the following exercises, plot each point in a rectangular coordinate system.
| 1. a) b) c) d) |
2. a) b) c) d) |
| 3. a) b) c) d) |
4. a) b) c) d) |
Identify Points on a Graph
In the following exercises, name the ordered pair of each point shown in the rectangular coordinate system.
5.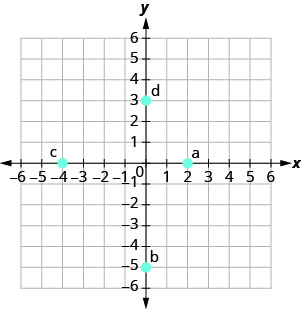 |
6.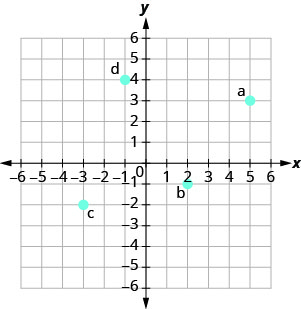 |
Verify Solutions to an Equation in Two Variables
In the following exercises, which ordered pairs are solutions to the given equations?
|
7. a) |
8. a) |
Complete a Table of Solutions to a Linear Equation in Two Variables
In the following exercises, complete the table to find solutions to each linear equation.
|
9.
|
10. |
||||||||||||||||||||||||
|
11.
|
12.
|
Find Solutions to a Linear Equation in Two Variables
In the following exercises, find three solutions to each linear equation.
| 13. |
14. |
| 15. |
16. |
Recognize the Relation Between the Solutions of an Equation and its Graph
In the following exercises, for each ordered pair, decide:
a) Is the ordered pair a solution to the equation?
b) Is the point on the line?
| 17.
|
18.
|
Graph a Linear Equation by Plotting Points
In the following exercises, graph by plotting points.
| 19. |
20. |
| 21. |
22. |
| 23. |
24. |
Graph Vertical and Horizontal lines
In the following exercises, graph each equation.
| 25. |
26. |
In the following exercises, graph each pair of equations in the same rectangular coordinate system.
| 27. |
28. |
Identify the x– and y-Intercepts on a Graph
In the following exercises, find the x– and y-intercepts.
29.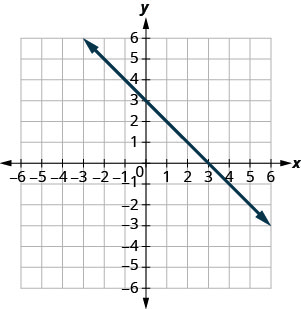 |
30. 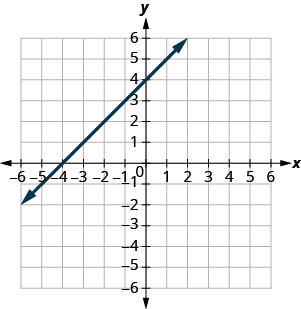 |
Find the x– and y-Intercepts from an Equation of a Line
In the following exercises, find the intercepts of each equation.
| 31. |
32. |
| 33. |
34. |
| 35. |
36. |
Graph a Line Using the Intercepts
In the following exercises, graph using the intercepts.
| 37. |
38. |
| 39. |
40. |
| 41. |
42. |
Use Geoboards to Model Slope
In the following exercises, find the slope modeled on each geoboard.
43. 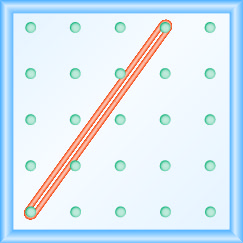 |
44. 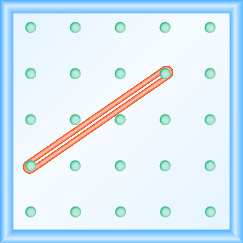 |
45. 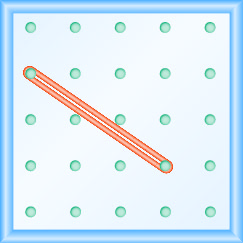 |
46. 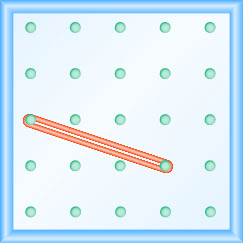 |
In the following exercises, model each slope. Draw a picture to show your results.
| 47. |
48. |
| 49. |
50. |
In the following exercises, find the slope of each line shown. Use ![]() to find the slope of a line from its graph.
to find the slope of a line from its graph.
51. 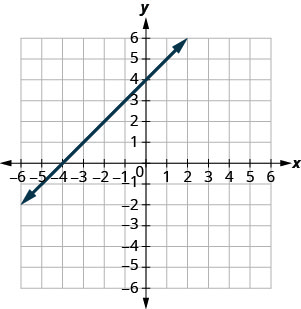 |
52. 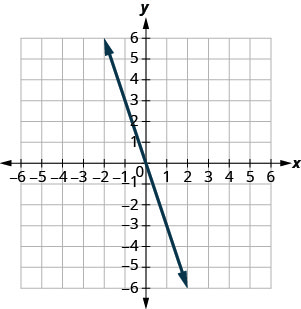 |
53. 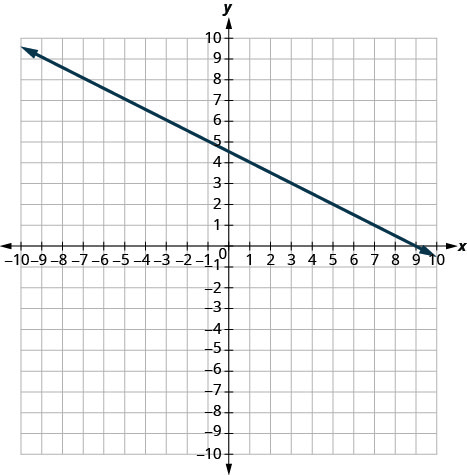 |
54. 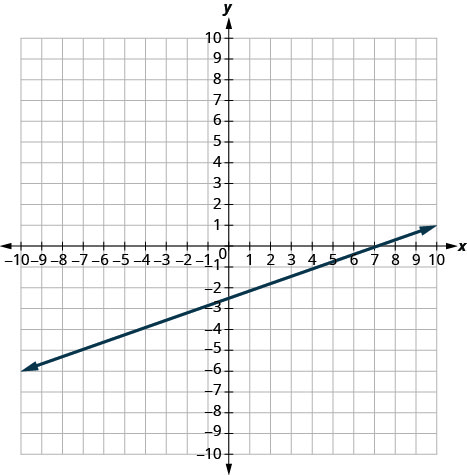 |
Find the Slope of Horizontal and Vertical Lines
In the following exercises, find the slope of each line.
| 55. |
56. |
| 57. |
58. |
Use the Slope Formula to find the Slope of a Line between Two Points
In the following exercises, use the slope formula to find the slope of the line between each pair of points.
| 59. |
60. |
| 61. |
62. |
Graph a Line Given a Point and the Slope
In the following exercises, graph each line with the given point and slope.
| 63. |
64. |
| 65. y-intercept 1; |
66. x-intercept |
Solve Slope Applications
In the following exercises, solve these slope applications.
| 67. A mountain road rises 50 feet for a 500-foot run. What is its slope? | 68. The roof pictured below has a rise of 10 feet and a run of 15 feet. What is its slope?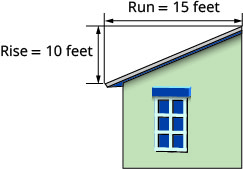 |
Recognize the Relation Between the Graph and the Slope–Intercept Form of an Equation of a Line
In the following exercises, use the graph to find the slope and y-intercept of each line. Compare the values to the equation ![]() .
.
| 69.
|
70.
|
Identify the Slope and y-Intercept from an Equation of a Line
In the following exercises, identify the slope and y-intercept of each line.
| 71. |
72. |
| 73. |
74. |
Graph a Line Using Its Slope and Intercept
In the following exercises, graph the line of each equation using its slope and y-intercept.
| 75. |
76. |
| 77. |
78. |
In the following exercises, determine the most convenient method to graph each line.
| 79. |
80. |
| 81. |
82. |
| 83. |
84. |
Graph and Interpret Applications of Slope–Intercept
|
85. Marjorie teaches piano. The equation
|
86. Katherine is a private chef. The equation
|
Use Slopes to Identify Parallel Lines
In the following exercises, use slopes and y-intercepts to determine if the lines are parallel.
| 87. |
88. |
Use Slopes to Identify Perpendicular Lines
In the following exercises, use slopes and y-intercepts to determine if the lines are perpendicular.
| 89. |
90. |
Find an Equation of the Line Given the Slope and y-Intercept
In the following exercises, find the equation of a line with given slope and y-intercept. Write the equation in slope–intercept form.
| 91. slope |
92. slope |
| 93. slope |
94. slope |
In the following exercises, find the equation of the line shown in each graph. Write the equation in slope–intercept form.
95. 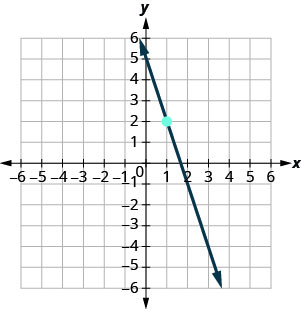 |
96. 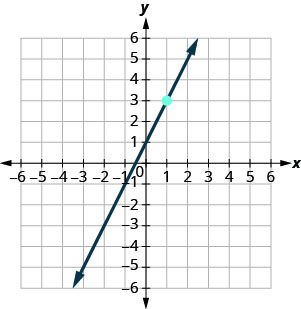 |
97. 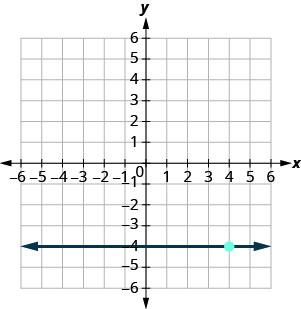 |
98. 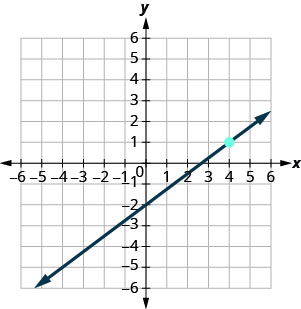 |
Find an Equation of the Line Given the Slope and a Point
In the following exercises, find the equation of a line with given slope and containing the given point. Write the equation in slope–intercept form.
| 99. |
100. |
| 101. |
102. Horizontal line containing |
Find an Equation of the Line Given Two Points
In the following exercises, find the equation of a line containing the given points. Write the equation in slope–intercept form.
| 103. |
104. |
| 105. |
106. |
Find an Equation of a Line Parallel to a Given Line
In the following exercises, find an equation of a line parallel to the given line and contains the given point. Write the equation in slope–intercept form.
| 107. line |
108. line |
| 109. line |
110. line |
Find an Equation of a Line Perpendicular to a Given Line
In the following exercises, find an equation of a line perpendicular to the given line and contains the given point. Write the equation in slope–intercept form.
| 112. line |
111. line |
| 114. line |
113. line |
Review Answers
1. 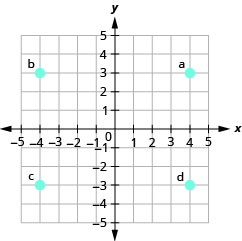 |
3. 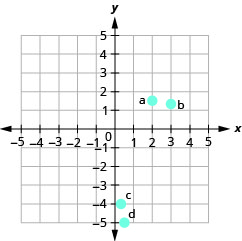 |
||||||||||||||||||||||||
| 5. a) |
7. a, b | ||||||||||||||||||||||||
9.
|
11.
|
||||||||||||||||||||||||
| 13. Answers will vary. | 15. Answers will vary. | ||||||||||||||||||||||||
| 17. a) yes; yes b) yes; no | 19.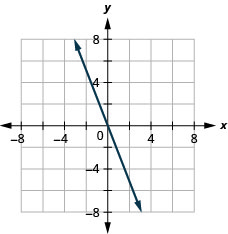 |
||||||||||||||||||||||||
21. 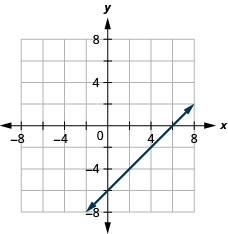 |
23. 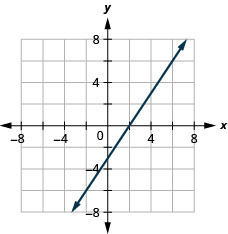 |
||||||||||||||||||||||||
25. 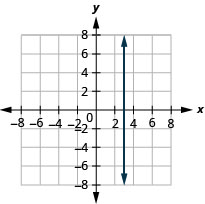 |
27. 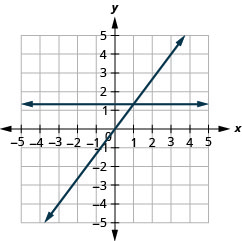 |
||||||||||||||||||||||||
| 29. |
31. |
||||||||||||||||||||||||
| 33. |
35. |
||||||||||||||||||||||||
37. 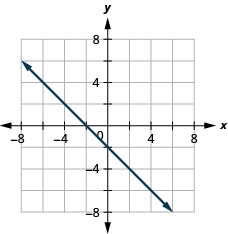 |
39. 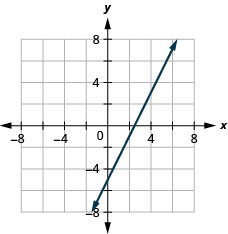 |
||||||||||||||||||||||||
41. 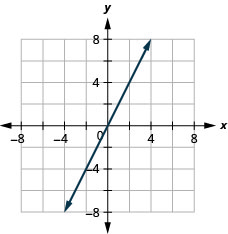 |
43. |
||||||||||||||||||||||||
| 45. |
47. 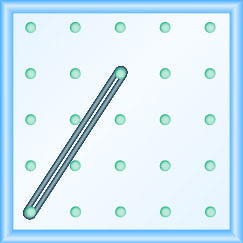 |
||||||||||||||||||||||||
49. 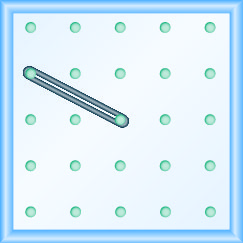 |
51. 1 | ||||||||||||||||||||||||
| 53. |
55. undefined | ||||||||||||||||||||||||
| 57. 0 | 59. |
||||||||||||||||||||||||
| 61. |
63. 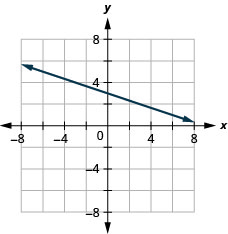 |
||||||||||||||||||||||||
65. 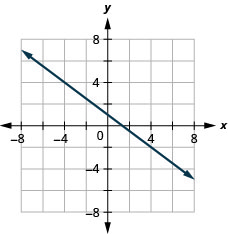 |
67. |
||||||||||||||||||||||||
| 69. slope |
71. |
||||||||||||||||||||||||
| 73. |
75. 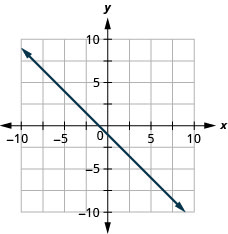 |
||||||||||||||||||||||||
77. 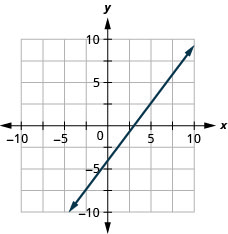 |
79. horizontal line | ||||||||||||||||||||||||
| 81. intercepts | 83. plotting points | ||||||||||||||||||||||||
85. a) −?250 b) ?450 c) The slope, 35, means that Marjorie’s weekly profit, P, increases by $35 for each additional student lesson she teaches. The P–intercept means that when the number of lessons is 0, Marjorie loses $250. d)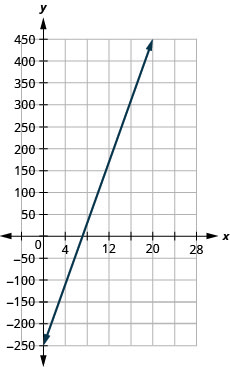 |
87. not parallel | ||||||||||||||||||||||||
| 89. perpendicular | 91. |
||||||||||||||||||||||||
| 93. |
95. |
||||||||||||||||||||||||
| 97. |
99. |
||||||||||||||||||||||||
| 101. |
103. |
||||||||||||||||||||||||
| 105. |
107. |
||||||||||||||||||||||||
| 109. |
111. |
||||||||||||||||||||||||
| 113. |
Practice Test
| 1. Plot each point in a rectangular coordinate system.
a) |
2. Which of the given ordered pairs are solutions to the equation a) |
| 3. Find three solutions to the linear equation |
4. Find the x– and y-intercepts of the equation |
Find the slope of each line shown.
5. 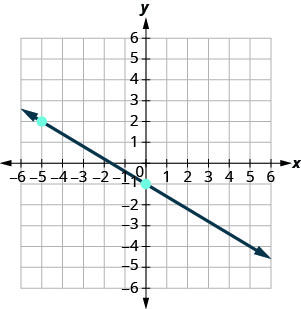 |
6. 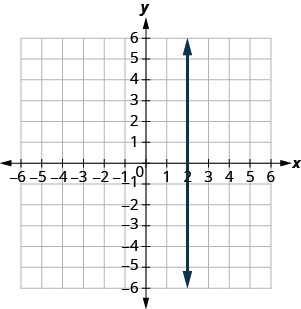 |
7. 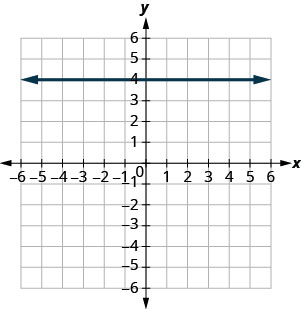 |
| 8. Find the slope of the line between the points |
9. Graph the line with slope |
Graph the line for each of the following equations
| 10. |
11. |
| 12. |
13. |
| 14. |
15. |
Find the equation of each line. Write the equation in slope–intercept form.
| 16. slope |
17. |
| 18. containing |
19. parallel to the line |
| 20. perpendicular to the line |
Practice Test Answers
1. 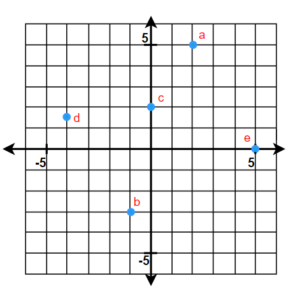 |
2. a) yes b) yes c) no |
| 3. Answer may vary | 4. |
| 5. m = |
6. undefined |
| 7. m = 0 | 8. |
| 9. y = |
10. 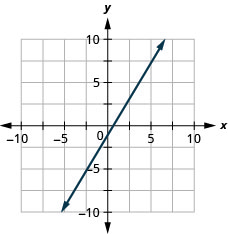 |
11. 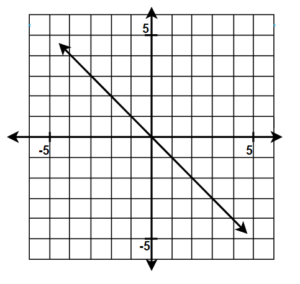 |
12.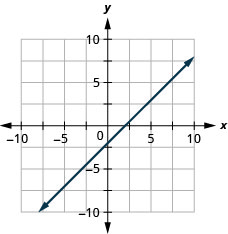 |
13. 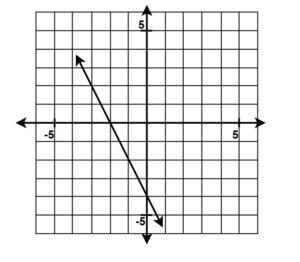 |
14.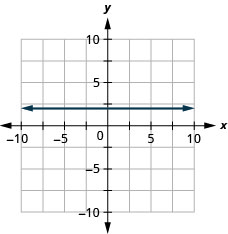 |
15. 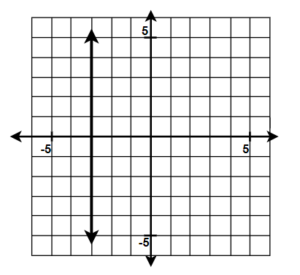 |
16. |
| 17. |
18. |
| 19. |
20. |
Attributions
This chapter has been adapted from “Review Exercises” and “Practice Test” in Chapter 4 of Elementary Algebra (OpenStax) by Lynn Marecek and MaryAnne Anthony-Smith, which is under a CC BY 4.0 Licence. Adapted by Izabela Mazur. See the Copyright page for more information.