CHAPTER 9 Trigonometry
9.2 Solve Applications: Sine, Cosine and Tangent Ratios.
Learning Objectives
By the end of this section, you will be able to:
- Find missing side of a right triangle using sine, cosine, or tangent ratios
- Find missing angle of a right triangle using sine, cosine, or tangent ratios
- Solve applications using right angle trigonometry
Sine, Cosine, and Tangent Ratios
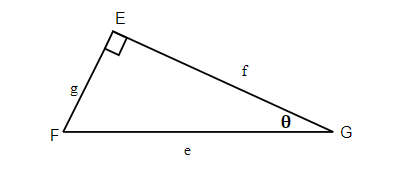
We know that any right triangle has three sides and a right angle. The side opposite to the right angle is called the hypotenuse. The other two angles in a right triangle are acute angles (with a measure less than 90 degrees). One of those angles we call reference angle and we use θ (theta) to represent it.
The hypotenuse is always the longest side of a right triangle. The other two sides are called opposite side and adjacent side. The names of those sides depends on which of the two acute angles is being used as a reference angle.
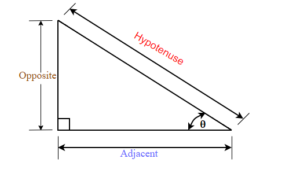
In the right triangle each side is labeled with a lowercase letter to match the uppercase letter of the opposite vertex.
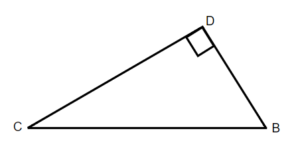
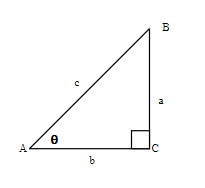
EXAMPLE 1
Label the sides of the triangle and find the hypotenuse, opposite, and adjacent.
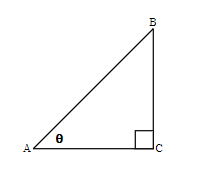
Solution
We labeled the sides with a lowercase letter to match the uppercase letter of the opposite vertex.
c is hypotenuse
a is opposite
b is adjacent
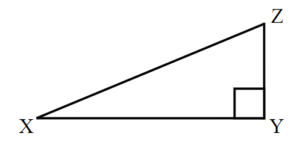
TRY IT 1.1
Label the sides of the triangle and find the hypotenuse, opposite and adjacent.
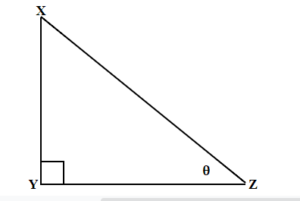
Show answer
y is hypotenuse
z is opposite
x is adjacent
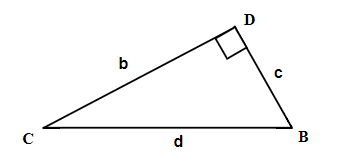
TRY IT 1.2
Label the sides of the triangle and find the hypotenuse, opposite and adjacent.
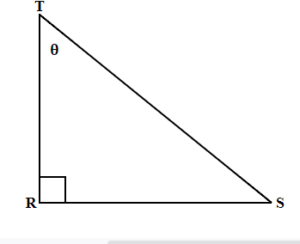
Show answer
r is hypotenuse
t is opposite
s is adjacent
Trigonometric Ratios
Trigonometric ratios are the ratios of the sides in the right triangle. For any right triangle we can define three basic trigonometric ratios: sine, cosine, and tangent.
Let us refer to Figure 1 and define the three basic trigonometric ratios as:
Three Basic Trigonometric Ratios
- sine θ =
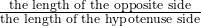
- cosine θ =
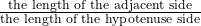
- tangent θ =
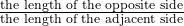
Where θ is the measure of a reference angle measured in degrees.
Very often we use the abbreviations for sine, cosine, and tangent ratios.
- sin θ =
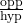
- cos θ =
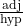
- tan θ =
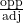
Some people remember the definition of the trigonometric ratios as SOH CAH TOA.
Let’s use the ![]() from Example 1 to find the three ratios.
from Example 1 to find the three ratios.
EXAMPLE 2
For the given triangle find the sine, cosine and tangent ratio.
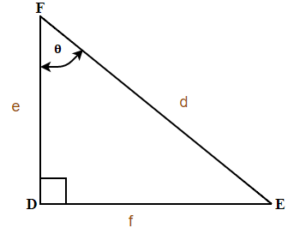
Solution
sin θ = ![]()
cos θ = ![]()
tan θ = ![]()
TRY IT 2.1
For the given triangle find the sine cosine and tangent ratio.

Show answer
sin θ = ![]()
cos θ = ![]()
tan θ = ![]()
TRY IT 2.2
For the given triangle find the sine, cosine and tangent ratio.

Show answer
sin θ = ![]()
cos θ = ![]()
tan θ = ![]()
In Example 2, our reference angles can be ![]() or
or ![]() . Using the definition of trigonometric ratios, we can write sinE=
. Using the definition of trigonometric ratios, we can write sinE=![]() , cosE=
, cosE=![]() , and tanE=
, and tanE= ![]() .
.
When calculating we will usually round the ratios to four decimal places and at the end our final answer to one decimal place unless stated otherwise.
EXAMPLE 3
For the given triangle find the sine, cosine and tangent ratios. If necessary round to four decimal places.
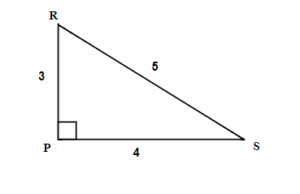
Solution
We have two possible reference angles: R an S.
Using the definitions, the trigonometric ratios for angle R are:
- sin R=
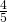 = 0.8
= 0.8 - cos R=
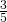 = 0.6
= 0.6 - tan R=
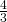 = 1.3333…
= 1.3333…
Using the definitions, the trigonometric ratios for angle S:
- sin S =
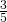 = 0.6
= 0.6 - cos S =
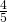 = 0.8
= 0.8 - tan S =
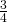 = 0.75
= 0.75
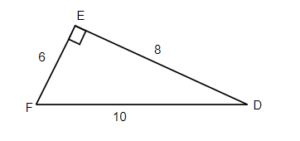
TRY IT 3.1
For the given triangle find the sine, cosine, and tangent ratios. If necessary round to four decimal places.
Show answer
- sin F =
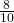 = 0.8
= 0.8 - cos F =
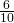 =0.6
=0.6 - tan F =
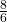 = 1.3333…
= 1.3333… - sin D =
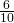 = 0.6
= 0.6 - cos D =
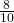 = 0.8
= 0.8 - tan D =
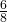 = 0.75
= 0.75
TRY IT 3.2
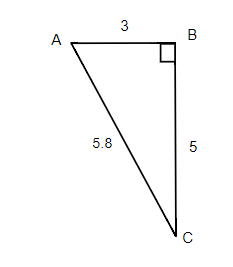
For given triangle find the sine, cosine and tangent ratios. If necessary round to four decimal places.
Show answer
- sin A =
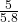 = 0.8621
= 0.8621 - cos A =
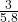 =0.5172
=0.5172 - tan A =
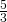 = 1.6667
= 1.6667 - sin C =
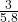 = 0.5172
= 0.5172 - cos C =
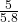 = 0.8621
= 0.8621 - tan C =
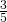 = 0.6
= 0.6
Now, let us use a scientific calculator to find the trigonometric ratios. Can you find the sin, cos, and tan buttons on your calculator? To find the trigonometric ratios make sure your calculator is in Degree Mode.
EXAMPLE 4
Using a calculator find the trigonometric ratios. If necessary, round to 4 decimal places.
a) sin 30°
b) cos 45°
c) tan 60°
Solution
Make sure your calculator is in Degree Mode.
a) Using a calculator find that sin 30° = 0.5
b) Using a calculator find that cos 45° = 0.7071 Rounded to 4 decimal places.
c) Using a calculator find that tan 60° = 1.7321 Rounded to 4 decimal places.
TRY IT 4.1
Find the trigonometric ratios. If necessary, round to 4 decimal places.
a) sin 60°
b) cos 30°
c) tan 45°
Show answer
a) sin 60° = 0.8660
b) cos 30° = 0.8660
c) tan 45° = 1
TRY IT 4.2
Find the trigonometric ratios. If necessary, round to 4 decimal places.
a) sin 35°
b) cos 67°
c) tan 83°
Show answer
a) sin 35° = 0.5736
b) cos 67 ° = 0.3907
c) tan 83° = 8.1443
Finding Missing Sides of a Right Triangle
In this section you will be using trigonometric ratios to solve right triangle problems. We will adapt our problem solving strategy for trigonometry applications. In addition, since those problems will involve the right triangle, it is helpful to draw it (if the drawing is not given) and label it with the given information.We will include this in the first step of the problem solving strategy for trigonometry applications.
HOW TO: Solve Trigonometry Applications
- Read the problem and make sure all the words and ideas are understood. Draw the right triangle and label the given parts.
- Identify what we are looking for.
- Label what we are looking for by choosing a variable to represent it.
- Find the required trigonometric ratio.
- Solve the ratio using good algebra techniques.
- Check the answer by substituting it back into the ratio in step 4 and by making sure it makes sense in the context of the problem.
- Answer the question with a complete sentence.
In the next few examples, having given the measure of one acute angle and the length of one side of the right triangle, we will solve the right triangle for the missing sides.
EXAMPLE 5
Find the missing sides. Round your final answer to two decimal places
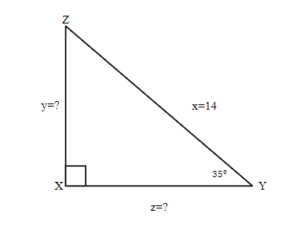
Solution
| 1. Read the problem and make sure all the words and ideas are understood. Draw the right triangle and label the given parts. | A drawing is given. Angle Y is our reference angle, y is opposite side, z is adjacent side, and x=14 is the hypotenuse. | |
| 2. Identify what we are looking for. | a) the opposite side | b) adjacent side |
| 3.Label what we are looking for by choosing a variable to represent it. | y=? | z=? |
| 4. Find the required trigonometric ratio. | sin 35° = |
cos 35° = |
| 5. Solve the ratio using good algebra techniques. | 14 sin 35° = y
8.03 = y |
14 cos 35° = z
11.47 = z |
| 6. Check the answer in the problem and by making sure it makes sense. | 0.57 0.57 = 0.57 |
0.82 0.82 = 0.82 |
| 7. Answer the question with a complete sentence. | The opposite side is 8.03 | The adjacent side is 11.47 |
TRY IT 5.1
Find the missing sides. Round your final answer to one decimal place.
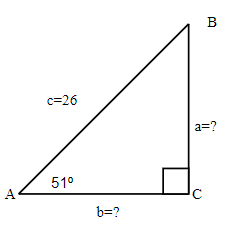
Show answer
a = 20.2
b = 16.4
TRY IT 5.2
Find the missing sides. Round your final answer to one decimal place.
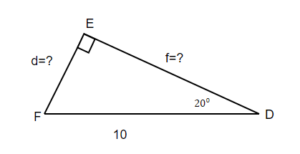
Show answer
d = 3.4
f = 9.4
EXAMPLE 6
Find the hypotenuse. Round your final answer to one decimal place.
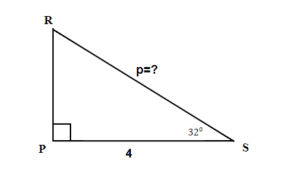
Solution
| 1. Read the problem and make sure all the words and ideas are understood. Draw the right triangle and label the given parts. | A drawing is given. Angle S is our reference angle, s is opposite side, r = 4 is the adjacent side, and p is the hypotenuse |
| 2. Identify what we are looking for. | the hypotenuse |
| 3.Label what we are looking for by choosing a variable to represent it. | p=? |
| 4. Find the required trigonometric ratio. | cos 32° = |
| 5. Solve the ratio using good algebra techniques. | 0.8480 = p = 4.7170 Rounding the ratios to 4 decimal places |
| 6. Check the answer in the problem and by making sure it makes sense. | 0.8480 0.8480 = 0.8480 |
| 7. Answer the question with a complete sentence. | The hypotenuse is 4.7
Round my final answer to one decimal place. |
TRY IT 6.1..
Find the hypotenuse. Round your final answer to one decimal place.
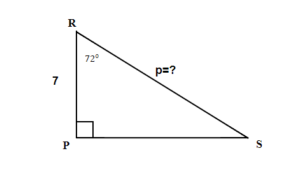
Show answer
p = 22.7
TRY IT 6.2
Find the hypotenuse. Round your final answer to one decimal place.
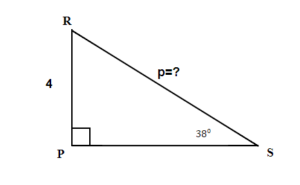
Show answer
p = 6.5
Finding Missing Angles of a Right Triangle
Sometimes we have a right triangle with only the sides given. How can we find the missing angles? To find the missing angles, we use the inverse of the trigonometric ratios. The inverse buttons sin-1, cos-1, and tan-1 are on your scientific calculator.
EXAMPLE 7
Find the angles. Round your final answer to one decimal place.
a) sin A = 0.5
b) cos B = 0.9735
c) tan C = 2.89358
Solution
Use your calculator and press the 2nd FUNCTION key and then press the SIN, COS, or TAN key
a) A = sin-10.5
![]() = 30°
= 30°
b) B = cos-10.9735
![]() = 13.2° Rounded to one decimal place
= 13.2° Rounded to one decimal place
c) C = tan-12.89358
![]() = 70.9° Rounded to one decimal place
= 70.9° Rounded to one decimal place
TRY IT 7.1
Find the angles. Round your final answer to one decimal place.
a) sin X = 1
b) cos Y = 0.375
c) tan Z = 1.676767
Show answer
a) ![]() = 90°
= 90°
b) ![]() = 68°
= 68°
c) ![]() = 59.2°
= 59.2°
TRY IT 7.2
Find the angles. Round your final answer to one decimal place.
a) sin C = 0
b) cos D = 0.95
c) tan F = 6.3333
Show answer
a) ![]() = 0°
= 0°
b) ![]() = 18.2°
= 18.2°
c) ![]() = 81°
= 81°
In the example below we have a right triangle with two sides given. Our acute angles are missing. Let us see what the steps are to find the missing angles.
EXAMPLE 8
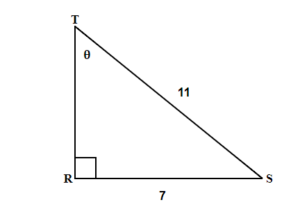
Find the missing ![]() . Round your final answer to one decimal place.
. Round your final answer to one decimal place.
Solution
| 1. Read the problem and make sure all the words and ideas are understood. Draw the right triangle and label the given parts. | A drawing is given. Angle T is our reference angle, t = 7 is the opposite side, s is adjacent side, and r =11 is the hypotenuse |
| 2. Identify what we are looking for. | angle T |
| 3.Label what we are looking for by choosing a variable to represent it. | |
| 4. Find the required trigonometric ratio. | sin T = |
| 5. Solve the ratio using good algebra techniques. | sin T = 0.6364
T = sin-10.6364
|
| 6. Check the answer in the problem and by making sure it makes sense. | sin 39.5239° 0.6364 = 0.6364 |
| 7. Answer the question with a complete sentence. | The missing angle T is 39.5°. |
TRY IT 8.1
Find the missing angle X. Round your final answer to one decimal place.
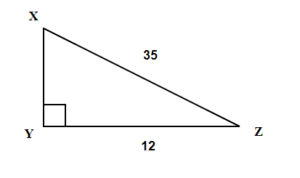
Show answer
20.1°
TRY IT 8.2
Find the missing angle Z. Round your final answer to one decimal place.

Show answer
69.9°
EXAMPLE 9
Find the missing angle A. Round your final answer to one decimal place.
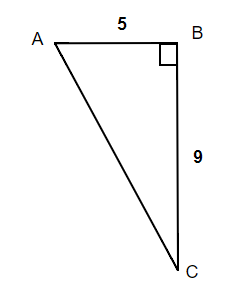
Solution
| 1. Read the problem and make sure all the words and ideas are understood. Draw the right triangle and label the given parts. | A drawing is given. Angle A is our reference angle, a = 9 is the opposite side, c = 5 is the adjacent side, and b is the hypotenuse |
| 2. Identify what we are looking for. | angle A |
| 3.Label what we are looking for by choosing a variable to represent it. | |
| 4. Find the required trigonometric ratio. | tan A = |
| 5. Solve the ratio using good algebra techniques. | tan A = 1.8
A = tan-1 1.8
|
| 6. Check the answer in the problem and by making sure it makes sense. | tan 60.9° 1.8 = 1.8 |
| 7. Answer the question with a complete sentence. | The missing angle A is 60.9°. |
TRY IT 9.1
Find the missing angle C. Round your final answer to one decimal place.

Show answer
29.1°
TRY IT 9.2
Find the missing angle E. Round your final answer to one decimal place.
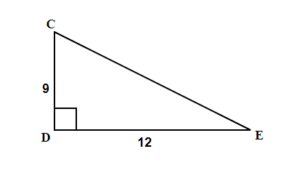
Show answer
36.9°
Solving a Right Triangle
From the section before we know that any triangle has three sides and three interior angles. In a right triangle, when all six parts of the triangle are known, we say that the right triangle is solved.
EXAMPLE 10
Solve the right triangle. Round your final answer to one decimal place.
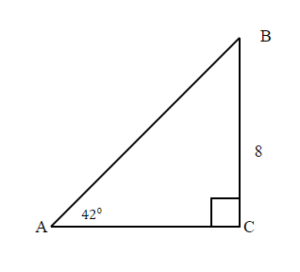
Solution
Since the sum of angles in any triangle is 180°, the measure of angle B can be easy calculated.
![]() = 180° − 90° − 42°
= 180° − 90° − 42°
![]() = 48°
= 48°
| 1. Read the problem and make sure all the words and ideas are understood. Draw the right triangle and label the given parts. | A drawing is given. Angle A is our reference angle, a = 8 is the opposite side, b is the adjacent side, and c is the hypotenuse. | |
| 2. Identify what we are looking for. | a) adjacent side | b) hypotenuse |
| 3.Label what we are looking for by choosing a variable to represent it. | b = ? | c = ? |
| 4. Find the required trigonometric ratio. | tan 42° = |
sin 42° = |
| 5. Solve the ratio using good algebra techniques. | 0.9004 = 0.9004 b = 8 b = 8.8849 |
0.6691 = 0.6691 c = 8 c = 11.9563 |
| 6. Check the answer in the problem and by making sure it makes sense. | tan 42 ° 0.9 = 0.9 |
sin 42° 0.6691 = 0.6691 |
| 7. Answer the question with a complete sentence. | The adjacent side is 8.9.
Rounded to one decimal place. |
The hypotenuse is 12 |
We solved the right triangle
![]() = 42°
= 42°
![]() = 48°
= 48°
![]() = 90°
= 90°
a = 8
b = 8.9
c = 12
TRY IT 10.1
Solve the right triangle. Round your final answer to one decimal place.
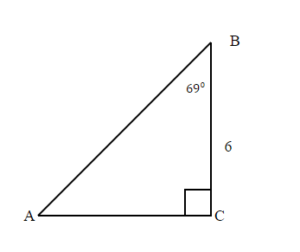
![]() = 21°
= 21°
![]() = 69°
= 69°
![]() = 90°
= 90°
Show answer
a = 6
b = 15.6
c = 16.7
TRY IT 10.2
Solve the right triangle. Round your final answer to one decimal place.
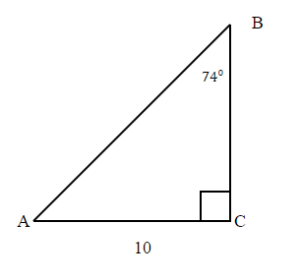
![]() =16°
=16°
![]() = 74°
= 74°
![]() = 90°
= 90°
Show answer
a = 2.9
b = 10
c = 10.4
EXAMPLE 11
Solve the right triangle. Round to two decimal places.
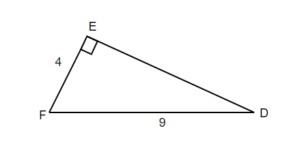
Solution
| 1. Read the problem and make sure all the words and ideas are understood. Draw the right triangle and label the given parts. | A drawing is given. Let angle D be our reference angle, d = 4 is the opposite side, f is the adjacent side, and e = 9 is the hypotenuse | |
| 2. Identify what we are looking for. | a) angle D | b) adjacent |
| 3.Label what we are looking for by choosing a variable to represent it. | f = ? | |
| 4. Find the required trigonometric ratio. | sin D = |
42 + f2 = 92 |
| 5. Solve the ratio using good algebra techniques. | sin D = 0.4444
D = sin-10.4444
|
16 + f2 = 81
f2 = 81 – 16 f2 = 65 f = square root of 65 f = 8.06 |
| 6. Check the answer in the problem and by making sure it makes sense. | sin 26.3850° 0.4444 =0.4444 |
42 + 8.062 81 = 81 |
| 7. Answer the question with a complete sentence. | The missing angle D is 26.39°. | The adjacent side is 8.06 Rounded to two decimal places |
The missing angle F = 180° – 90° – 26.39° = 63.64°
We solved the right triangle
![]() = 26.39°
= 26.39°
![]() = 90°
= 90°
![]() = 63.61°
= 63.61°
d = 4
e = 9
f = 8.06
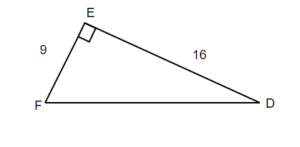
TRY IT 11.1
Solve the right triangle. Round to one decimal place.
![]() = 29.3°
= 29.3°
![]() = 90°
= 90°
![]() = 60.7°
= 60.7°
Show answer
d = 29.4
e = 18.4
f = 60.6
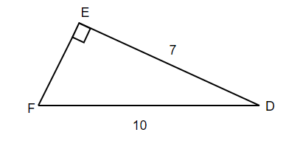
TRY IT 11.2
Solve the right triangle. Round to one decimal place.
![]() = 45.6°
= 45.6°
![]() = 90°
= 90°
![]() = 44.4°
= 44.4°
Show answer
d = 7.1
e = 10
f = 7
Solve Applications Using Trigonometric Ratios
In the previous examples we were able to find missing sides and missing angles of a right triangle. Now, let’s use the trigonometric ratios to solve real-life problems.
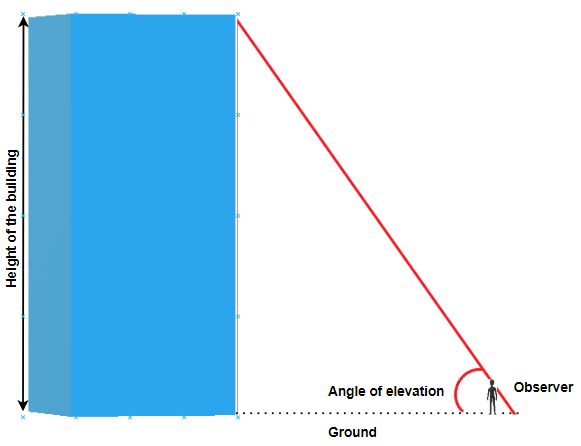
Many applications of trigonometric ratios involve understanding of an angle of elevation or angle of depression.
The angle of elevation is an angle between the horizontal line (ground) and the observer’s line of sight.
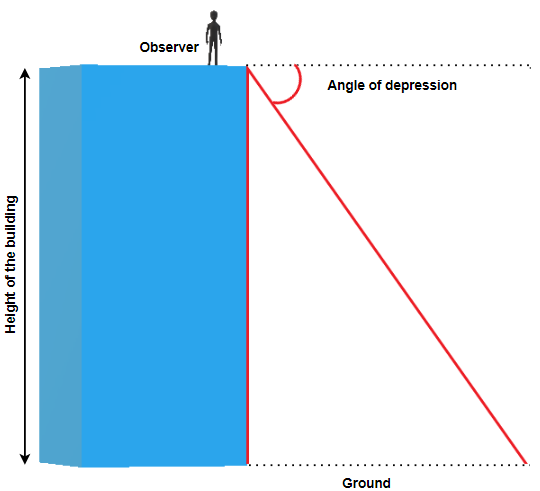
The angle of depression is the angle between horizontal line (that is parallel to the ground) and the observer’s line of sight.
EXAMPLE 12
James is standing 31 metres away from the base of the Harbour Centre in Vancouver. He looks up to the top of the building at a 78° angle. How tall is the Harbour Centre?
Solution
| 1. Read the problem and make sure all the words and ideas are understood. Draw the right triangle and label the given parts. | 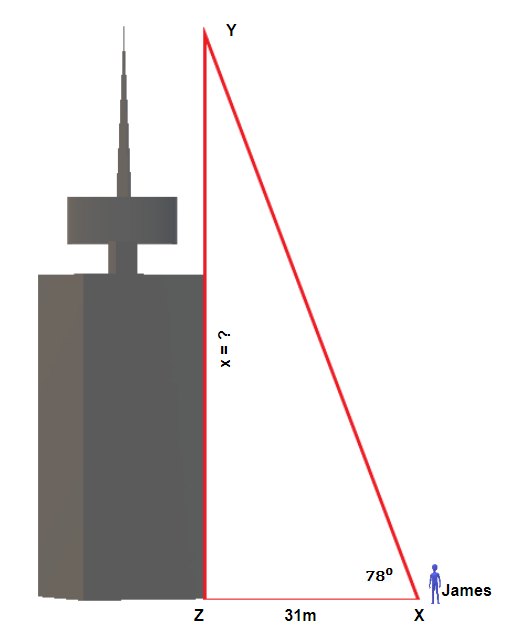
Angle X is our reference angle, x is opposite side, y = 31 m is the adjacent side, and z is the hypotenuse. |
| 2. Identify what we are looking for. | The opposite side |
| 3.Label what we are looking for by choosing a variable to represent it. | x=? |
| 4. Find the required trigonometric ratio. | tan 78° = |
| 5. Solve the ratio using good algebra techniques. | 4.7046 = x = 145.8426 |
| 6. Check the answer in the problem and by making sure it makes sense. | 4.7046 4.7046 = 4.7046 |
| 7. Answer the question with a complete sentence. | The Harbour Centre is 145.8426 metres or rounded to 146 metres. |
TRY IT 12.1
Nicole is standing 75 feet away from the base of the Living Shangri-La, the tallest building in British Columbia. She looks up to the top of the building at a 83.5° angle. How tall is the Living Shangri-La?
Show answer
658.3 feet.
TRY IT 12.2
Kelly is standing 23 metres away from the base of the tallest apartment building in Prince George and looks at the top of the building at a 62° angle. How tall is the building?
Show answer
43.3 metres
EXAMPLE 13
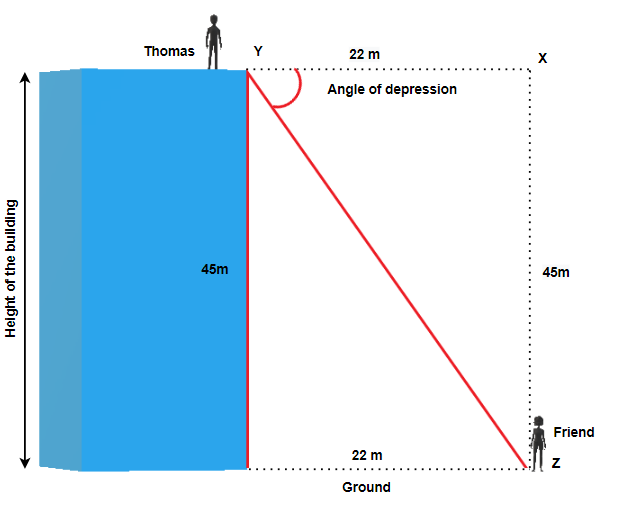
Thomas is standing at the top of the building that is 45 metres high and looks at his friend that is standing on the ground, 22 metres from the base of the building. What is the angle of depression?
Solution
| 1. Read the problem and make sure all the words and ideas are understood. Draw the right triangle and label the given parts. |
Angle Y is our reference angle, y = 45 m is the opposite side, z = 22 m is the adjacent side, and x is the hypotenuse |
| 2. Identify what we are looking for. | angle Y |
| 3.Label what we are looking for by choosing a variable to represent it. | |
| 4. Find the required trigonometric ratio. | tan Y = |
| 5. Solve the ratio using good algebra techniques. | tan Y = 2.0455
Y = tan –¹2.0455
|
| 6. Check the answer in the problem and by making sure it makes sense. | tan 63.9470° 2.0455 = 2.0455 |
| 7. Answer the question with a complete sentence. | The angle of depression is 63.9470° or 64° rounded to one decimal place. |
TRY IT 13.1
Hemanth is standing on the top of a cliff 250 feet above the ground and looks at his friend that is standing on the ground, 40 feet from the base of the cliff. What is the angle of depression?
Show answer
80.9°
TRY IT 13.2
Klaudia is standing on the ground, 25 metres from the base of the cliff and looks up at her friend on the top of a cliff 100 metres above the ground. What is the angle of elevation?
Show answer
76°
Key Concepts
- Three Basic Trigonometric Ratios: (Where θ is the measure of a reference angle measured in degrees.)
- sine θ =
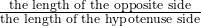
- cosine θ =
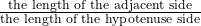
- tangent θ =
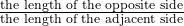
- sine θ =
- Problem-Solving Strategy for Trigonometry Applications
- Read the problem and make sure all the words and ideas are understood. Draw the right triangle and label the given parts.
- Identify what we are looking for.
- Label what we are looking for by choosing a variable to represent it.
- Find the required trigonometric ratio.
- Solve the ratio using good algebra techniques.
- Check the answer by substituting it back into the ratio solved in step 5 and by making sure it makes sense in the context of the problem.
- Answer the question with a complete sentence.
Practice Makes Perfect
Label the sides of the triangle.
| 1
|
2.
|
| 3. If the reference angle in Question 1 is B, Find the adjacent ?
|
4. If the reference angle in Question 2 is Z, find the opposite ? |
Label the sides of the triangle and find the hypotenuse, opposite and adjacent.
5.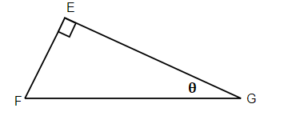 |
6.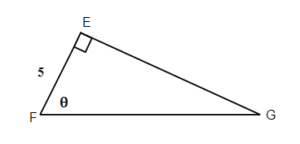 |
Use your calculator to find the given ratios. Round to four decimal places if necessary:
| 7. |
8. |
| 9. |
10. |
For the given triangles, find the sine, cosine and tangent of the θ.
11.  |
12.  |
13. 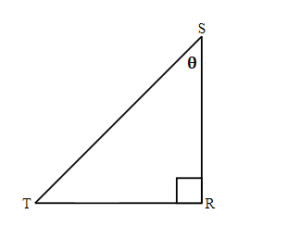 |
14. 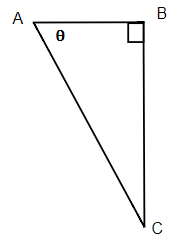 |
For the given triangles, find the missing side. Round it to one decimal place.
15. Find the hypotenuse.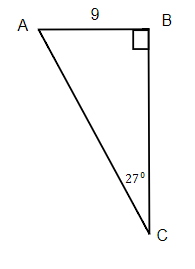 |
16. Find b if a = 6. 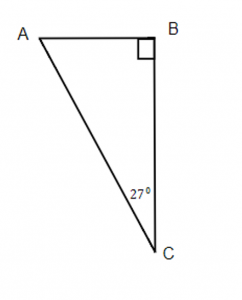 |
17. Find the opposite. 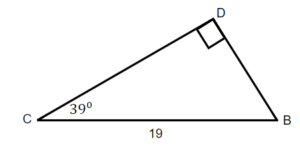 |
18. Find the adjacent. 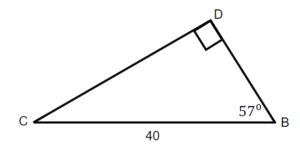 |
For the given triangles, find the missing sides. Round it to one decimal place.
19. 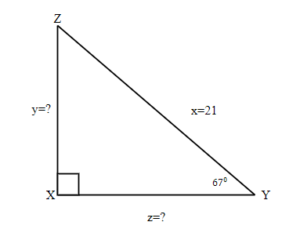 |
20. 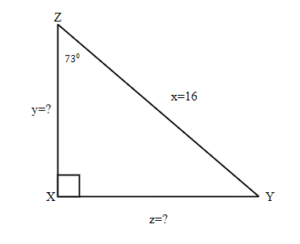 |
Solve the triangles. Round to one decimal place.
21. 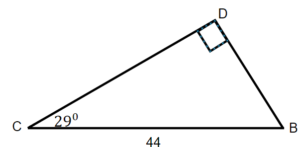 |
22. 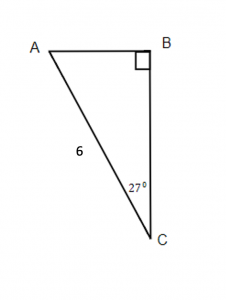 |
23. 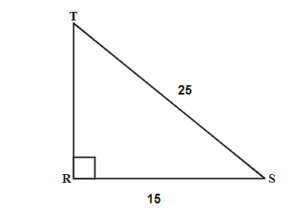 |
24. 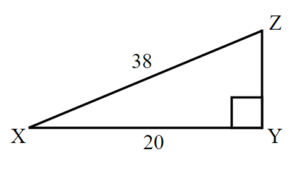 |
| 25. A surveyor stands 75 metres from the bottom of a tree and looks up at the top of the tree at a 48° angle. How tall is the tree? | 26. A tree makes a shadow that is 6 metres long when the angle of elevation to the sun is 52°. How tall is the tree? |
| 27. A ladder that is 15 feet is leaning against a house and makes a 45° angle with the ground. How far is the base of the ladder from the house? | 28. Matt is flying a kite and has let out 100 feet of string. The angle of elevation with the ground is 38°. How high is his kite above the ground? |
| 29. Marta is flying a kite and has let out 28 metres of string. If the kite is 10 metres above the ground, what is the angle of elevation? | 30. An airplane takes off from the ground at the angle of 25°. If the airplane traveled 200 kilometres, how high above the ground is it? |
Answers
| 1.
|
3. c | 5.
g is opposite , f is adjacent, and e is hypotenuse |
| 7. 0.7314 | 9. 0.2126 | 11.
sin θ = |
| 13. sin θ = |
15. b = 19.8 | 17. c = 12 |
| 19. y = 19.3, z = 8.2 | 21.
b = 38.5 c = 21.3 d = 44 |
23.
t = 15 r = 25 s = 20 |
| 25. 83.3 m | 27. 10.6 ft | 29. 20.9° |