CHAPTER 4 Ratio, Proportion, and Percent
4.1 Ratios and Rate
Learning Objectives
By the end of this section, you will be able to:
- Write a ratio as a fraction
- Find unit rates
- Find unit price
- Translate phrases to expressions with fractions
Write a Ratio as a Fraction
Ratios
A ratio compares two numbers or two quantities that are measured with the same unit. The ratio of ![]() to
to ![]() is written
is written ![]()
In this section, we will use the fraction notation. When a ratio is written in fraction form, the fraction should be simplified. If it is an improper fraction, we do not change it to a mixed number. Because a ratio compares two quantities, we would leave a ratio as ![]() instead of simplifying it to
instead of simplifying it to ![]() so that we can see the two parts of the ratio.
so that we can see the two parts of the ratio.
EXAMPLE 1
Write each ratio as a fraction: a)![]() b)
b)![]() .
.
| Write as a fraction with the first number in the numerator and the second in the denominator. | |
| Simplify the fraction. |
We leave the ratio in b) as an improper fraction.
| Write as a fraction with the first number in the numerator and the second in the denominator. | |
| Simplify. |
TRY IT 1.1
Write each ratio as a fraction: a) ![]() b)
b) ![]() .
.
Show answer
TRY IT 1.2
Write each ratio as a fraction: a)![]() b)
b) ![]() .
.
Show answer
Ratios Involving Decimals
We will often work with ratios of decimals, especially when we have ratios involving money. In these cases, we can eliminate the decimals by using the Equivalent Fractions Property to convert the ratio to a fraction with whole numbers in the numerator and denominator.
For example, consider the ratio ![]() . We can write it as a fraction with decimals and then multiply the numerator and denominator by
. We can write it as a fraction with decimals and then multiply the numerator and denominator by ![]() to eliminate the decimals.
to eliminate the decimals.

Do you see a shortcut to find the equivalent fraction? Notice that ![]() and
and ![]() . The least common denominator of
. The least common denominator of ![]() and
and ![]() is
is ![]() . By multiplying the numerator and denominator of
. By multiplying the numerator and denominator of ![]() by
by ![]() , we ‘moved’ the decimal two places to the right to get the equivalent fraction with no decimals. Now that we understand the math behind the process, we can find the fraction with no decimals like this:
, we ‘moved’ the decimal two places to the right to get the equivalent fraction with no decimals. Now that we understand the math behind the process, we can find the fraction with no decimals like this:
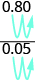 |
|
| “Move” the decimal 2 places. | |
| Simplify. |
You do not have to write out every step when you multiply the numerator and denominator by powers of ten. As long as you move both decimal places the same number of places, the ratio will remain the same.
EXAMPLE 2
Write each ratio as a fraction of whole numbers:
a) ![]()
b) ![]()
| a)
|
|
| Write as a fraction. | |
| Rewrite as an equivalent fraction without decimals, by moving both decimal points 1 place to the right. | |
| Simplify. |
So ![]() is equivalent to
is equivalent to ![]() .
.
| b) The numerator has one decimal place and the denominator has |
|
| Write as a fraction. | |
| Move both decimals right two places. | |
| Simplify. |
So ![]() is equivalent to
is equivalent to ![]() .
.
TRY IT 2.1
Write each ratio as a fraction: a) ![]() b)
b) ![]() .
.
Show answer
TRY IT 2.2
Write each ratio as a fraction: a) ![]() b)
b) ![]() .
.
Show answer
Some ratios compare two mixed numbers. Remember that to divide mixed numbers, you first rewrite them as improper fractions.
EXAMPLE 3
Write the ratio of ![]() as a fraction.
as a fraction.
| Write as a fraction. | |
| Convert the numerator and denominator to improper fractions. | |
| Rewrite as a division of fractions. | |
| Invert the divisor and multiply. | |
| Simplify. |
TRY IT 3.1
Write each ratio as a fraction: ![]() .
.
Show answer
![]()
TRY IT 3.2
Write each ratio as a fraction: ![]() .
.
Show answer
![]()
Applications of Ratios
One real-world application of ratios that affects many people involves measuring cholesterol in blood. The ratio of total cholesterol to HDL cholesterol is one way doctors assess a person’s overall health. A ratio of less than ![]() to 1 is considered good.
to 1 is considered good.
EXAMPLE 4
Hector’s total cholesterol is ![]() mg/dl and his HDL cholesterol is
mg/dl and his HDL cholesterol is ![]() mg/dl. a) Find the ratio of his total cholesterol to his HDL cholesterol. b) Assuming that a ratio less than
mg/dl. a) Find the ratio of his total cholesterol to his HDL cholesterol. b) Assuming that a ratio less than ![]() to
to ![]() is considered good, what would you suggest to Hector?
is considered good, what would you suggest to Hector?
a) First, write the words that express the ratio. We want to know the ratio of Hector’s total cholesterol to his HDL cholesterol.
| Write as a fraction. | |
| Substitute the values. | |
| Simplify. |
b) Is Hector’s cholesterol ratio ok? If we divide ![]() by
by ![]() we obtain approximately
we obtain approximately ![]() , so
, so ![]() . Hector’s cholesterol ratio is high! Hector should either lower his total cholesterol or raise his HDL cholesterol.
. Hector’s cholesterol ratio is high! Hector should either lower his total cholesterol or raise his HDL cholesterol.
TRY IT 4.1
Find the patient’s ratio of total cholesterol to HDL cholesterol using the given information.
Total cholesterol is ![]() mg/dL and HDL cholesterol is
mg/dL and HDL cholesterol is ![]() mg/dL.
mg/dL.
Show answer
![]()
TRY IT 4.2
Find the patient’s ratio of total cholesterol to HDL cholesterol using the given information.
Total cholesterol is ![]() mg/dL and HDL cholesterol is
mg/dL and HDL cholesterol is ![]() mg/dL.
mg/dL.
Show answer
![]()
Ratios of Two Measurements in Different Units
To find the ratio of two measurements, we must make sure the quantities have been measured with the same unit. If the measurements are not in the same units, we must first convert them to the same units.
We know that to simplify a fraction, we divide out common factors. Similarly in a ratio of measurements, we divide out the common unit.
EXAMPLE 5
The Canadian National Building Code (CNBC) Guidelines for wheel chair ramps require a maximum vertical rise of ![]() inch for every
inch for every ![]() foot of horizontal run. What is the ratio of the rise to the run?
foot of horizontal run. What is the ratio of the rise to the run?
In a ratio, the measurements must be in the same units. We can change feet to inches, or inches to feet. It is usually easier to convert to the smaller unit, since this avoids introducing more fractions into the problem.
Write the words that express the ratio.
| Ratio of the rise to the run | |
| Write the ratio as a fraction. | |
| Substitute in the given values. | |
| Convert 1 foot to inches. | |
| Simplify, dividing out common factors and units. |
So the ratio of rise to run is ![]() to
to ![]() . This means that the ramp should rise
. This means that the ramp should rise ![]() inch for every
inch for every ![]() inches of horizontal run to comply with the guidelines.
inches of horizontal run to comply with the guidelines.
TRY IT 5.1
Find the ratio of the first length to the second length: ![]() inches to
inches to ![]() foot.
foot.
Show answer
![]()
TRY IT 5.2
Find the ratio of the first length to the second length: ![]() foot to
foot to ![]() inches.
inches.
Show answer
![]()
Write a Rate as a Fraction
Frequently we want to compare two different types of measurements, such as miles to gallons. To make this comparison, we use a rate. Examples of rates are ![]() miles in
miles in ![]() hours,
hours, ![]() words in
words in ![]() minutes, and
minutes, and ![]() dollars per
dollars per ![]() ounces.
ounces.
Rate
A rate compares two quantities of different units. A rate is usually written as a fraction.
When writing a fraction as a rate, we put the first given amount with its units in the numerator and the second amount with its units in the denominator. When rates are simplified, the units remain in the numerator and denominator.
EXAMPLE 6
Bob drove his car ![]() miles in
miles in ![]() hours. Write this rate as a fraction.
hours. Write this rate as a fraction.
| Write as a fraction, with 525 miles in the numerator and 9 hours in the denominator. | |
So ![]() miles in
miles in ![]() hours is equivalent to
hours is equivalent to ![]() .
.
TRY IT 6.1
Write the rate as a fraction: ![]() miles in
miles in ![]() hours.
hours.
Show answer
![]()
TRY IT 6.2
Write the rate as a fraction: ![]() miles in
miles in ![]() hours.
hours.
Show answer
![]()
Find Unit Rates
In the last example, we calculated that Bob was driving at a rate of ![]() . This tells us that every three hours, Bob will travel
. This tells us that every three hours, Bob will travel ![]() miles. This is correct, but not very useful. We usually want the rate to reflect the number of miles in one hour. A rate that has a denominator of
miles. This is correct, but not very useful. We usually want the rate to reflect the number of miles in one hour. A rate that has a denominator of ![]() unit is referred to as a unit rate.
unit is referred to as a unit rate.
Unit Rate
A unit rate is a rate with denominator of ![]() unit.
unit.
Unit rates are very common in our lives. For example, when we say that we are driving at a speed of ![]() miles per hour we mean that we travel
miles per hour we mean that we travel ![]() miles in
miles in ![]() hour. We would write this rate as
hour. We would write this rate as ![]() miles/hour (read
miles/hour (read ![]() miles per hour). The common abbreviation for this is
miles per hour). The common abbreviation for this is ![]() mph. Note that when no number is written before a unit, it is assumed to be
mph. Note that when no number is written before a unit, it is assumed to be ![]() .
.
So ![]() miles/hour really means
miles/hour really means ![]()
Two rates we often use when driving can be written in different forms, as shown:
| Example | Rate | Write | Abbreviate | Read |
|---|---|---|---|---|
Another example of unit rate that you may already know about is hourly pay rate. It is usually expressed as the amount of money earned for one hour of work. For example, if you are paid ![]() for each hour you work, you could write that your hourly (unit) pay rate is
for each hour you work, you could write that your hourly (unit) pay rate is ![]() (read
(read ![]() per hour.)
per hour.)
To convert a rate to a unit rate, we divide the numerator by the denominator. This gives us a denominator of ![]() .
.
EXAMPLE 7
Anita was paid ![]() last week for working
last week for working ![]() . What is Anita’s hourly pay rate?
. What is Anita’s hourly pay rate?
| Start with a rate of dollars to hours. Then divide. | |
| Write as a rate. | |
| Divide the numerator by the denominator. | |
| Rewrite as a rate. |
Anita’s hourly pay rate is ![]() per hour.
per hour.
TRY IT 7.1
Find the unit rate: ![]() for
for ![]() hours.
hours.
Show answer
$18.00/hour
TRY IT 7.2
Find the unit rate: ![]() for
for ![]() hours.
hours.
Show answer
$19.00/hour
EXAMPLE 8
Sven drives his car ![]() miles, using
miles, using ![]() gallons of gasoline. How many miles per gallon does his car get?
gallons of gasoline. How many miles per gallon does his car get?
Start with a rate of miles to gallons. Then divide.
| Write as a rate. | |
| Divide 455 by 14 to get the unit rate. |
Sven’s car gets ![]() miles/gallon, or
miles/gallon, or ![]() mpg.
mpg.
TRY IT 8.1
Find the unit rate: ![]() miles to
miles to ![]() gallons of gas.
gallons of gas.
Show answer
23.5 mpg
TRY IT 8.2
Find the unit rate: ![]() miles to
miles to ![]() gallons of gas.
gallons of gas.
Show answer
28 mpg
Find Unit Price
Sometimes we buy common household items ‘in bulk’, where several items are packaged together and sold for one price. To compare the prices of different sized packages, we need to find the unit price. To find the unit price, divide the total price by the number of items. A unit price is a unit rate for one item.
Unit price
A unit price is a unit rate that gives the price of one item.
EXAMPLE 9
The grocery store charges ![]() for a case of
for a case of ![]() bottles of water. What is the unit price?
bottles of water. What is the unit price?
What are we asked to find? We are asked to find the unit price, which is the price per bottle.
| Write as a rate. | |
| Divide to find the unit price. | |
| Round the result to the nearest penny. |
The unit price is approximately ![]() per bottle. Each bottle costs about
per bottle. Each bottle costs about ![]() .
.
TRY IT 9.1
Find the unit price. Round your answer to the nearest cent if necessary.
![]() of juice boxes for
of juice boxes for ![]()
Show answer
$0.29/box
TRY IT 9.2
Find the unit price. Round your answer to the nearest cent if necessary.
![]() of bottles of ice tea for
of bottles of ice tea for ![]()
Show answer
$0.53/bottle
Unit prices are very useful if you comparison shop. The better buy is the item with the lower unit price. Most grocery stores list the unit price of each item on the shelves.
EXAMPLE 10
Paul is shopping for laundry detergent. At the grocery store, the liquid detergent is priced at ![]() for
for ![]() loads of laundry and the same brand of powder detergent is priced at
loads of laundry and the same brand of powder detergent is priced at ![]() for
for ![]() loads.
loads.
Which is the better buy, the liquid or the powder detergent?
To compare the prices, we first find the unit price for each type of detergent.
| Liquid | Powder | |
| Write as a rate. | ||
| Find the unit price. | ||
| Round to the nearest cent. |
Now we compare the unit prices. The unit price of the liquid detergent is about ![]() per load and the unit price of the powder detergent is about
per load and the unit price of the powder detergent is about ![]() per load. The powder is the better buy.
per load. The powder is the better buy.
TRY IT 10.1
Find each unit price and then determine the better buy. Round to the nearest cent if necessary.
Brand A Storage Bags, ![]() for
for ![]() count, or Brand B Storage Bags,
count, or Brand B Storage Bags, ![]() for
for ![]() count
count
Show answer
Brand A costs $0.12 per bag. Brand B costs $0.13 per bag. Brand A is the better buy.
TRY IT 10.2
Find each unit price and then determine the better buy. Round to the nearest cent if necessary.
Brand C Chicken Noodle Soup, ![]() for
for ![]() ounces, or Brand D Chicken Noodle Soup,
ounces, or Brand D Chicken Noodle Soup, ![]() for
for ![]() ounces
ounces
Show answer
Brand C costs $0.07 per ounce. Brand D costs $0.09 per ounce. Brand C is the better buy.
Notice in the above example that we rounded the unit price to the nearest cent. Sometimes we may need to carry the division to one more place to see the difference between the unit prices.
Translate Phrases to Expressions with Fractions
Have you noticed that the examples in this section used the comparison words ratio of, to, per, in, for, on, and from? When you translate phrases that include these words, you should think either ratio or rate. If the units measure the same quantity (length, time, etc.), you have a ratio. If the units are different, you have a rate. In both cases, you write a fraction.
EXAMPLE 11
Translate the word phrase into an algebraic expression:
a) ![]() miles per
miles per ![]() hours
hours
b) ![]() students to
students to ![]() teachers
teachers
c) ![]() dollars for
dollars for ![]() hours
hours
| a) | |
| Write as a rate. |
| b) | |
| Write as a rate. |
| c) | |
| Write as a rate. |
TRY IT 11.1
Translate the word phrase into an algebraic expression.
a) ![]() miles per
miles per ![]() hours b)
hours b) ![]() parents to
parents to ![]() students c)
students c) ![]() dollars for
dollars for ![]() minutes
minutes
Show answer
- 689 mi/h hours
- y parents/22 students
- $d/9 min
TRY IT 11.2
Translate the word phrase into an algebraic expression.
a)![]() miles per
miles per ![]() hours b)
hours b) ![]() students to
students to ![]() buses c)
buses c) ![]() dollars for
dollars for ![]() hours
hours
Show answer
- m mi/9 h
- x students/8 buses
- $y/40 h
Access to Additional Online R
Glossary
- ratio
- A ratio compares two numbers or two quantities that are measured with the same unit. The ratio of
 to
to 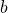 is written
is written  to
to 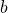 ,
, 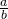 , or
, or 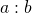 .
.
- rate
- A rate compares two quantities of different units. A rate is usually written as a fraction.
- unit rate
- A unit rate is a rate with denominator of 1 unit.
- unit price
- A unit price is a unit rate that gives the price of one item.
Practice Makes Perfect
Write a Ratio as a Fraction
In the following exercises, write each ratio as a fraction.
| 1. |
2. |
| 3. |
4. |
| 5. |
6. |
| 7. |
8. |
| 9. |
10. |
| 11. |
12. |
| 13. |
14. |
| 15. |
16. |
| 17. |
18. |
| 19. |
20. |
| 21. |
22. |
| 23. |
24. |
| 25. total cholesterol of |
26. total cholesterol of |
| 27. |
28. |
Write a Rate as a Fraction
In the following exercises, write each rate as a fraction.
| 29. |
30. |
| 31. |
32. |
| 33. |
34. |
| 35. |
36. |
Find Unit Rates
In the following exercises, find the unit rate. Round to two decimal places, if necessary.
| 37. |
38. |
| 39. |
40. |
| 41. |
42. |
| 43. |
44. |
| 45. |
46. |
| 47. |
48. |
| 49. |
50. |
| 51. The bindery at a printing plant assembles |
52. The pressroom at a printing plant prints |
Find Unit Price
In the following exercises, find the unit price. Round to the nearest cent.
| 53. Soap bars at |
54. Soap bars at |
| 55. Women’s sports socks at |
56. Men’s dress socks at |
| 57. Snack packs of cookies at |
58. Granola bars at |
| 59. CD-RW discs at |
60. CDs at |
| 61. The grocery store has a special on macaroni and cheese. The price is |
62. The pet store has a special on cat food. The price is |
In the following exercises, find each unit price and then identify the better buy. Round to three decimal places.
| 63. Mouthwash, |
64. Toothpaste, |
| 65. Breakfast cereal, |
66. Breakfast Cereal, |
| 67. Ketchup, |
68. Mayonnaise |
| 69. Cheese |
70. Candy |
Translate Phrases to Expressions with Fractions
In the following exercises, translate the English phrase into an algebraic expression.
| 71. |
72. |
| 73. |
74. |
| 75. 105 calories in |
76. |
| 77. the ratio of |
78. the ratio of |
Everyday Math
| 79. One elementary school in Saskatchewan has |
80. The average Canadian produces about |
| 81. A popular fast food burger weighs |
82. A |
Writing Exercises
| 83. Would you prefer the ratio of your income to your friend’s income to be |
84. The parking lot at the airport charges |
| 85. Kathryn ate a |
86. Arjun had a |
Answers
| 1. |
3. |
5. |
| 7. |
9. |
11. |
| 13. |
15. |
17. |
| 19. |
21. |
23. |
| 25. |
27. |
29. |
| 31. |
33. |
35. |
| 37. 11.67 calories/ounce | 39. 2.73 lbs./sq. in. | 41. 69.71 mph |
| 43. $14.88/hour | 45. 32 mpg | 47. 2.69 lbs./week |
| 49. 92 beats/minute | 51. 8,000 | 53. $1.09/bar |
| 55. $1.33/pair | 57. $0.48/pack | 59. $0.60/disc |
| 61. $1.29/box | 63. The 50.7-ounce size costs $0.138 per ounce. The 33.8-ounce size costs $0.142 per ounce. The 50.7-ounce size is the better buy. | 65. The 18-ounce size costs $0.222 per ounce. The 14-ounce size costs $0.235 per ounce. The 18-ounce size is a better buy. |
| 67. The regular bottle costs $0.075 per ounce. The squeeze bottle costs $0.069 per ounce. The squeeze bottle is a better buy. | 69. The half-pound block costs $6.78/lb, so the 1-lb. block is a better buy. | 71. |
| 73. |
75. |
77. |
| 79. 15.2 students per teacher | 81. a) 72 calories/ounce
b) 3.87 grams of fat/ounce c) 5.73 grams carbs/once d) 3.33 grams protein/ounce |
83. Answers will vary. |
| 85. Answers will vary. |
Attributions
This chapter has been adapted from “Ratios and Rate” in Prealgebra (OpenStax) by Lynn Marecek, MaryAnne Anthony-Smith, and Andrea Honeycutt Mathis, which is under a CC BY 4.0 Licence. Adapted by Izabela Mazur. See the Copyright page for more information.

