CHAPTER 7 Powers, Roots, and Scientific Notation
7.1 Use Multiplication Properties of Exponents
Learning Objectives
By the end of this section, you will be able to:
- Simplify expressions with exponents
- Simplify expressions using the Product Property for Exponents
- Simplify expressions using the Power Property for Exponents
- Simplify expressions using the Product to a Power Property
- Simplify expressions by applying several properties
- Multiply monomials
Simplify Expressions with Exponents
Remember that an exponent indicates repeated multiplication of the same quantity. For example, ![]() means to multiply 2 by itself 4 times, so
means to multiply 2 by itself 4 times, so ![]() means 2 · 2 · 2 · 2
means 2 · 2 · 2 · 2
Let’s review the vocabulary for expressions with exponents.
Exponential Notation
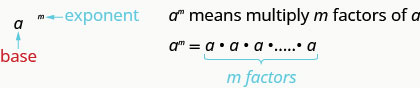
This is read ![]() to the
to the ![]() power.
power.
In the expression ![]() , the exponent
, the exponent ![]() tells us how many times we use the base
tells us how many times we use the base ![]() as a factor.
as a factor.

Before we begin working with variable expressions containing exponents, let’s simplify a few expressions involving only numbers.
EXAMPLE 1
Simplify: a) ![]() b)
b) ![]() c)
c) ![]() d)
d) ![]() .
.
| a) | |
| Multiply three factors of 4. | 4 · 4 · 4 |
| Simplify. | |
| b) | |
| Multiply one factor of 7. | |
| c) | |
| Multiply two factors. | |
| Simplify. | |
| d) | |
| Multiply two factors. | |
| Simplify. |
TRY IT 1.1
Simplify: a) ![]() b)
b) ![]() c)
c) ![]() d)
d) ![]() .
.
Show answer
a) 216 b) ![]() c)
c) ![]() d) 0.1849
d) 0.1849
TRY IT 1.2
Simplify: a) ![]() b)
b) ![]() c)
c) ![]() d)
d) ![]() .
.
Show answer
a) ![]() b) 21 c)
b) 21 c) ![]() d)
d) ![]()
EXAMPLE 2
Simplify: a) ![]() b)
b) ![]() .
.
| a) | |
| Multiply four factors of |
|
| Simplify. | |
| b) | |
| Multiply four factors of 5. | -(5 · 5 · 5 · 5) |
| Simplify. |
TRY IT 2.1
Simplify: a) ![]() b)
b) ![]() .
.
Show answer
a) ![]() b)
b) ![]()
TRY IT 2.2
Simplify: a) ![]() b)
b) ![]() .
.
Show answer
a) ![]() b)
b) ![]()
Notice the similarities and differences in (Example 2) a) and (Example 2) b)! Why are the answers different? As we follow the order of operations in part a) the parentheses tell us to raise the ![]() to the 4th power. In part b) we raise just the 5 to the 4th power and then take the opposite.
to the 4th power. In part b) we raise just the 5 to the 4th power and then take the opposite.
Simplify Expressions Using the Product Property for Exponents
You have seen that when you combine like terms by adding and subtracting, you need to have the same base with the same exponent. But when you multiply and divide, the exponents may be different, and sometimes the bases may be different, too.
We’ll derive the properties of exponents by looking for patterns in several examples.
First, we will look at an example that leads to the Product Property.
 |
|
| What does this mean? How many factors altogether? |
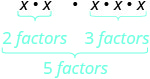 |
| So, we have | 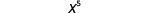 |
| Notice that 5 is the sum of the exponents, 2 and 3. | 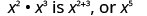 |
We write:
The base stayed the same and we added the exponents. This leads to the Product Property for Exponents.
Product Property for Exponents
If ![]() is a real number, and
is a real number, and ![]() and
and ![]() are counting numbers, then
are counting numbers, then
To multiply with like bases, add the exponents.
An example with numbers helps to verify this property.
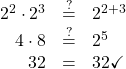
EXAMPLE 3
Simplify: ![]() .
.
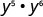 |
|
| Use the product property, am \cdot an = am+n. |  |
| Simplify. | 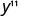 |
TRY IT 3.1
Simplify: ![]() .
.
Show answer
![]()
TRY IT 3.2
Simplify: ![]() .
.
Show answer
![]()
EXAMPLE 4
Simplify: a) ![]() b)
b) ![]() .
.
-

Use the product property, am · an = am+n. 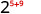
Simplify. 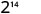
-
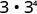
Use the product property, am · an = am+n. 
Simplify. 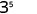
TRY IT 4.1
Simplify: a) ![]() b)
b) ![]() .
.
Show answer
a) ![]() b)
b) ![]()
TRY IT 4.2
Simplify: a) ![]() b)
b) ![]() .
.
Show answer
a) ![]() b)
b) ![]()
EXAMPLE 5
Simplify: a) ![]() b)
b) ![]() .
.
-
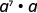
Rewrite, a = a1. 
Use the product property, am · an = am+n. 
Simplify. 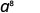
-

Notice, the bases are the same, so add the exponents. 
Simplify. 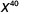
TRY IT 5.1
Simplify: a) ![]() b)
b) ![]() .
.
Show answer
a) ![]() b)
b) ![]()
TRY IT 5.2
Simplify: a) ![]() b)
b) ![]() .
.
Show answer
a) ![]() b)
b) ![]()
We can extend the Product Property for Exponents to more than two factors.
EXAMPLE 6
Simplify: ![]() .
.
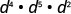 |
|
| Add the exponents, since bases are the same. |  |
| Simplify. |  |
TRY IT 6.1
Simplify: ![]() .
.
Show answer
![]()
TRY IT 6.2
Simplify: ![]() .
.
Show answer
![]()
Simplify Expressions Using the Power Property for Exponents
Now let’s look at an exponential expression that contains a power raised to a power. See if you can discover a general property.
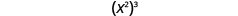 |
|
| What does this mean? How many factors altogether? |
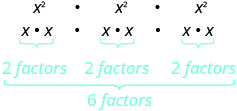 |
| So we have | 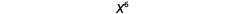 |
| Notice that 6 is the product of the exponents, 2 and 3. | 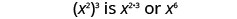 |
We write:
We multiplied the exponents. This leads to the Power Property for Exponents.
Power Property for Exponents
If ![]() is a real number, and
is a real number, and ![]() and
and ![]() are whole numbers, then
are whole numbers, then
![]()
To raise a power to a power, multiply the exponents.
An example with numbers helps to verify this property.
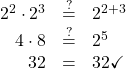
EXAMPLE 7
Simplify: a) ![]() b)
b) ![]() .
.
a)
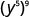 |
|
| Use the power property, (am)n = am · n. |  |
| Simplify. | 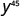 |
b)
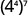 |
|
| Use the power property. |  |
| Simplify. | 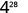 |
TRY IT 7.1
Simplify: a) ![]() b)
b) ![]() .
.
Show answer
a) ![]() b)
b) ![]()
TRY IT 7.2
Simplify: a) ![]() b)
b) ![]() .
.
Show answer
a) ![]() b)
b) ![]()
Simplify Expressions Using the Product to a Power Property
We will now look at an expression containing a product that is raised to a power. Can you find this pattern?
| What does this mean? | |
| We group the like factors together. | |
| How many factors of 2 and of |
Notice that each factor was raised to the power and ![]() is
is ![]() .
.
| We write: | |
The exponent applies to each of the factors! This leads to the Product to a Power Property for Exponents.
Product to a Power Property for Exponents
If ![]() and
and ![]() are real numbers and
are real numbers and ![]() is a whole number, then
is a whole number, then
![]()
To raise a product to a power, raise each factor to that power.
An example with numbers helps to verify this property:
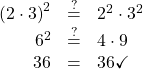
EXAMPLE 8
Simplify: a) ![]() b)
b) ![]() .
.
-
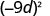
Use Power of a Product Property, (ab)m = ambm. 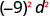
Simplify. 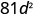
-
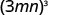
Use Power of a Product Property, (ab)m = ambm. 
Simplify. 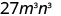
TRY IT 8.1
Simplify: a) ![]() b)
b) ![]() .
.
Show answer
a) ![]() b)
b) ![]()
TRY IT 8.2
Simplify: a) ![]() b)
b) ![]() .
.
Show answer
a) ![]() b)
b) ![]()
Simplify Expressions by Applying Several Properties
We now have three properties for multiplying expressions with exponents. Let’s summarize them and then we’ll do some examples that use more than one of the properties.
Properties of Exponents
If ![]() and
and ![]() are real numbers, and
are real numbers, and ![]() and
and ![]() are whole numbers, then
are whole numbers, then
| Product Property | |
| Power Property | |
| Product to a Power |
All exponent properties hold true for any real numbers![]() and
and ![]() . Right now, we only use whole number exponents.
. Right now, we only use whole number exponents.
EXAMPLE 9
Simplify: a) ![]() b)
b) ![]() .
.
| a) | |
| Use the Power Property. | |
| Add the exponents. | |
| b) | |
| Use the Product to a Power Property. | |
| Use the Power Property. | |
| Simplify. |
TRY IT 9.1
Simplify: a) ![]() b)
b) ![]() .
.
Show answer
a) ![]() b)
b) ![]()
TRY IT 9.2
Simplify: a) ![]() b)
b) ![]() .
.
Show answer
a) ![]() b)
b) ![]()
EXAMPLE 10
Simplify: a) ![]() b)
b) ![]() .
.
| a) | |
| Raise |
|
| Simplify. | |
| Use the Commutative Property. | |
| Multiply the constants and add the exponents. | |
| b) | |
| Use the Product to a Power Property. | |
| Simplify. | |
| Use the Commutative Property. | |
| Multiply the constants and add the exponents. |
TRY IT 10.1
Simplify: a) ![]() b)
b) ![]() .
.
Show answer
a) ![]() b)
b) ![]()
TRY IT 10.2
Simplify: a) ![]() b)
b) ![]() .
.
Show answer
a) ![]() b)
b) ![]()
Multiply Monomials
A term in algebra is a constant or the product of a constant and one or more variables. When it is of the form ![]() , where
, where ![]() is a constant and
is a constant and ![]() is a whole number, it is called a monomial. Some examples of monomial are
is a whole number, it is called a monomial. Some examples of monomial are ![]() , and
, and ![]() .
.
Monomials
A monomial is a term of the form ![]() , where
, where ![]() is a constant and
is a constant and ![]() is a positive whole number.
is a positive whole number.
Since a monomial is an algebraic expression,we can use the properties of exponents to multiply monomials.
EXAMPLE 11
Multiply: ![]() .
.
| Use the Commutative Property to rearrange the terms. | |
| Multiply. |
TRY IT 11.1
Multiply: ![]() .
.
Show answer
![]()
TRY IT 11.2
Multiply: ![]() .
.
Show answer
![]()
EXAMPLE 12
Multiply: ![]() .
.
| Use the Commutative Property to rearrange the terms. | |
| Multiply. |
TRY IT 12.1
Multiply: ![]() .
.
Show answer
![]()
TRY IT 12.2
Multiply: ![]() .
.
Show answer
![]()
Additional Online Resources
Key Concepts
- Exponential Notation
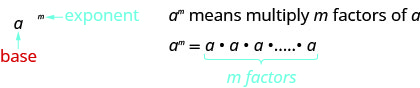
- Properties of Exponents
- If
 are real numbers and
are real numbers and 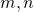 are whole numbers, then
are whole numbers, then
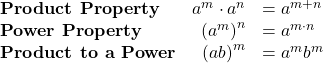
- If
Practice Makes Perfect
Simplify Expressions with Exponents
In the following exercises, simplify each expression with exponents.
|
1. a) |
2. a) |
|
3. a) |
4. a) |
|
5. a) |
6. a) |
|
7. a) |
8. a) |
|
9. a) |
10. a) |
Simplify Expressions Using the Product Property for Exponents
In the following exercises, simplify each expression using the Product Property for Exponents.
| 11. |
12. |
| 13. |
14. |
| 15. a) |
16. a) |
| 17. a) |
17. a) |
| 19. |
20. |
| 21. |
22. |
| 23. |
24. |
| 25. |
26. |
Simplify Expressions Using the Power Property for Exponents
In the following exercises, simplify each expression using the Power Property for Exponents.
| 27. a) |
28. a) |
| 29. a) |
30. a) |
Simplify Expressions Using the Product to a Power Property
In the following exercises, simplify each expression using the Product to a Power Property.
| 31. a) |
32. a) |
| 33. a) |
34. a) |
Simplify Expressions by Applying Several Properties
In the following exercises, simplify each expression.
|
35. a) |
36. a) |
|
37. a) |
38. a) |
|
39. a) |
40. a) |
|
41. a) |
42. a) |
|
43. a) |
44. a) |
|
45. a) |
Multiply Monomials
In the following exercises, multiply the terms.
| 46. |
47. |
| 48. |
49. |
| 50. |
51. |
| 52. |
53. |
| 54. |
55. |
| 56. |
56. |
Mixed Practice
In the following exercises, simplify each expression.
| 58. |
59. |
| 60. |
61. |
| 62. |
63. |
| 64. |
65. |
| 66. |
67. |
| 68. |
69. |
| 70. |
71. |
| 72. |
73. |
| 74. |
75. |
| 76. |
77. |
Everyday Math
|
78. Email Kate emails a flyer to ten of her friends and tells them to forward it to ten of their friends, who forward it to ten of their friends, and so on. The number of people who receive the email on the second round is
|
79. Salary Jamal’s boss gives him a 3% raise every year on his birthday. This means that each year, Jamal’s salary is 1.03 times his last year’s salary. If his original salary was $35,000, his salary after 1 year was
|
||||||||||||||||||||||||
|
80. Clearance A department store is clearing out merchandise in order to make room for new inventory. The plan is to mark down items by 30% each week. This means that each week the cost of an item is 70% of the previous week’s cost. If the original cost of a sofa was $1,000, the cost for the first week would be
|
81. Depreciation Once a new car is driven away from the dealer, it begins to lose value. Each year, a car loses 10% of its value. This means that each year the value of a car is 90% of the previous year’s value. If a new car was purchased for ?20,000, the value at the end of the first year would be
|
Writing Exercises
| 82. Use the Product Property for Exponents to explain why |
83. Explain why |
| 84. Jorge thinks |
85. Explain why |
Answers
| 2. a) 10,000 b) 17 c) |
4. a) 512 b) 8 c) |
| 6. a) 64 b) |
8. a) |
| 10. a) |
12. |
| 14. |
16. a) |
| 18. a) |
20. |
| 22. |
24. |
| 26. |
28. a) |
| 30. a) |
32. a) |
| 34. a) |
36. a) |
| 38. a) |
40. a) |
| 42. a) |
44. a) |
| 46. |
48. |
| 50. |
52. |
| 54. |
56. |
| 58. |
60. |
| 62. |
64. |
| 66. |
68. |
| 70. |
72. |
| 74. |
76. |
| 78. |
80. $168.07 |
| 82. Answers will vary. | 84. Answers will vary. |
Attributions
This chapter has been adapted from “Use Multiplication Properties of Exponents” in Prealgebra (OpenStax) by Lynn Marecek, MaryAnne Anthony-Smith, and Andrea Honeycutt Mathis, which is under a CC BY 4.0 Licence. Adapted by Izabela Mazur. See the Copyright page for more information.

