CHAPTER 3 Measurement, Perimeter, Area, and Volume
3.1 Systems of Measurement
Learning Objectives
By the end of this section, you will be able to:
- Make unit conversions in the imperial system
- Use mixed units of measurement in the imperial system
- Make unit conversions in the metric system
- Use mixed units of measurement in the metric system
- Convert between the imperial and the metric systems of measurement
- Convert between Fahrenheit and Celsius temperatures
Make Unit Conversions in the Imperial System
There are two systems of measurement commonly used around the world. Most countries use the metric system. Canada uses the metric system, and the United States use the imperial system of measurement. However, people in Canada often use imperial measurements as well. We will look at the imperial system first.
The imperial system of measurement uses units of inch, foot, yard, and mile to measure length and pound and ton to measure weight. For capacity, the units used are cup, pint, quart, and gallons. Both the imperial system and the metric system measure time in seconds, minutes, and hours.
The equivalencies of measurements are shown in the table below. The table also shows, in parentheses, the common abbreviations for each measurement.
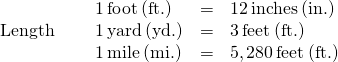 |
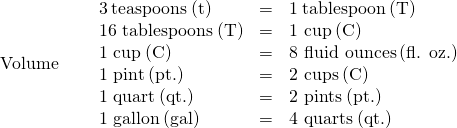 |
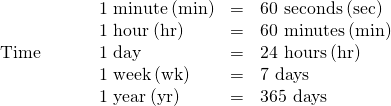 |
In many real-life applications, we need to convert between units of measurement, such as feet and yards, minutes and seconds, quarts and gallons, etc. We will use the identity property of multiplication to do these conversions. We’ll restate the identity property of multiplication here for easy reference.
Identity Property of Multiplication
For any real number ![]() :
:
![]()
![]()
1 is the multiplicative identity.
To use the identity property of multiplication, we write 1 in a form that will help us convert the units. For example, suppose we want to change inches to feet. We know that 1 foot is equal to 12 inches, so we will write 1 as the fraction ![]() . When we multiply by this fraction we do not change the value, but just change the units.
. When we multiply by this fraction we do not change the value, but just change the units.
But ![]() also equals 1. How do we decide whether to multiply by
also equals 1. How do we decide whether to multiply by ![]() or
or ![]() ? We choose the fraction that will make the units we want to convert from divide out. Treat the unit words like factors and “divide out” common units like we do common factors. If we want to convert
? We choose the fraction that will make the units we want to convert from divide out. Treat the unit words like factors and “divide out” common units like we do common factors. If we want to convert ![]() inches to feet, which multiplication will eliminate the inches?
inches to feet, which multiplication will eliminate the inches?

The inches divide out and leave only feet. The second form does not have any units that will divide out and so will not help us.
EXAMPLE 1
MaryAnne is 66 inches tall. Convert her height into feet.




TRY IT 1.1
Lexie is 30 inches tall. Convert her height to feet.
Show answer
2.5 feet
TRY IT 1.2
Rene bought a hose that is 18 yards long. Convert the length to feet.
Show answer
54 feet
HOW TO: Make unit conversions
- Multiply the measurement to be converted by 1; write 1 as a fraction relating the units given and the units needed.
- Multiply.
- Simplify the fraction.
- Simplify.
When we use the identity property of multiplication to convert units, we need to make sure the units we want to change from will divide out. Usually this means we want the conversion fraction to have those units in the denominator.
EXAMPLE 2
A female orca in the Salish Sea weighs almost 3.2 tons. Convert her weight to pounds.
We will convert 3.2 tons into pounds. We will use the identity property of multiplication, writing 1 as the fraction ![]() .
.
| Multiply the measurement to be converted, by 1. | |
| Write 1 as a fraction relating tons and pounds. | |
| Simplify. | 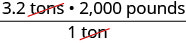 |
| Multiply. | |
| The female orca weighs almost 6,400 pounds. |
TRY IT 2.1
Arnold’s SUV weighs about 4.3 tons. Convert the weight to pounds.
Show answer
8,600 pounds
TRY IT 2.2
The Carnival Destiny cruise ship weighs 51,000 tons. Convert the weight to pounds.
Show answer
102,000,000 pounds
Sometimes, to convert from one unit to another, we may need to use several other units in between, so we will need to multiply several fractions.
EXAMPLE 3
Juliet is going with her family to their summer home. She will be away from her boyfriend for 9 weeks. Convert the time to minutes.
Solution
To convert weeks into minutes we will convert weeks into days, days into hours, and then hours into minutes. To do this we will multiply by conversion factors of 1.
| 9 weeks | |
| Write 1 as |
|
| Divide out the common units. | |
| Multiply. | |
| Multiply. |
Juliet and her boyfriend will be apart for 90,720 minutes (although it may seem like an eternity!).
TRY IT 3.1
The distance between the earth and the moon is about 250,000 miles. Convert this length to yards.
Show answer
440,000,000 yards
TRY IT 3.2
The astronauts of Expedition 28 on the International Space Station spend 15 weeks in space. Convert the time to minutes.
Show answer
151,200 minutes
EXAMPLE 4
How many ounces are in 1 gallon?
We will convert gallons to ounces by multiplying by several conversion factors. Refer to the table on Imperial Systems of Measurement.
| 1 gallon | |
| Multiply the measurement to be converted by 1. | |
| Use conversion factors to get to the right unit. Simplify. |
|
| Multiply. | |
| Simplify. | There are 128 ounces in a gallon. |
TRY IT 4.1
How many cups are in 1 gallon?
Show answer
16 cups
TRY IT 4.2
How many teaspoons are in 1 cup?
Show answer
48 teaspoons
Use Mixed Units of Measurement in the Imperial System
We often use mixed units of measurement in everyday situations. Suppose Joe is 5 feet 10 inches tall, stays at work for 7 hours and 45 minutes, and then eats a 1 pound 2 ounce steak for dinner—all these measurements have mixed units.
Performing arithmetic operations on measurements with mixed units of measures requires care. Be sure to add or subtract like units!
EXAMPLE 5
Seymour bought three steaks for a barbecue. Their weights were 14 ounces; 1 pound, 2 ounces; and 1 pound, 6 ounces. How many total pounds of steak did he buy?
We will add the weights of the steaks to find the total weight of the steaks.
| Add the ounces. Then add the pounds. |  |
| Convert 22 ounces to pounds and ounces. | 1 pound, 6 ounces |
| Add the pounds and ounces. | 2 pounds + 1 pound + 6 ounces |
| Answer | Seymour bought 3 pounds 6 ounces of steak. |
TRY IT 5.1
Laura gave birth to triplets weighing 3 pounds 3 ounces, 3 pounds 3 ounces, and 2 pounds 9 ounces. What was the total birth weight of the three babies?
Show answer
9 lbs. 8 oz
TRY IT 5.2
Stan cut two pieces of crown molding for his family room that were 8 feet 7 inches and 12 feet 11 inches. What was the total length of the molding?
Show answer
21 ft. 6 in.
EXAMPLE 6
Anthony bought four planks of wood that were each 6 feet 4 inches long. What is the total length of the wood he purchased?
We will multiply the length of one plank to find the total length.
| Multiply the inches and then the feet. | 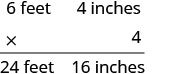 |
| Convert the 16 inches to feet. Add the feet. |
 |
| Anthony bought 25 feet and 4 inches of wood. |
TRY IT 6.1
Henri wants to triple his vegan spaghetti sauce recipe that uses 1 pound 8 ounces of black beans. How many pounds of black beans will he need?
Show answer
4 lbs. 8 oz.
TRY IT 6.2
Joellen wants to double a solution of 5 gallons 3 quarts. How many gallons of solution will she have in all?
Show answer
11 gallons 2 qt.
Make Unit Conversions in the Metric System
In the metric system, units are related by powers of 10. The roots words of their names reflect this relation. For example, the basic unit for measuring length is a metre. One kilometre is 1,000 metres; the prefix kilo means thousand. One centimetre is ![]() of a metre, just like one cent is
of a metre, just like one cent is ![]() of one dollar.
of one dollar.
The equivalencies of measurements in the metric system are shown in the table below. The common abbreviations for each measurement are given in parentheses.
| Length | Mass | Capacity |
|---|---|---|
| 1 kilometre (km) = 1,000 m
1 hectometre (hm) = 100 m 1 dekametre (dam) = 10 m 1 metre (m) = 1 m 1 decimetre (dm) = 0.1 m 1 centimetre (cm) = 0.01 m 1 millimetre (mm) = 0.001 m |
1 kilogram (kg) = 1,000 g
1 hectogram (hg) = 100 g 1 dekagram (dag) = 10 g 1 gram (g) = 1 g 1 decigram (dg) = 0.1 g 1 centigram (cg) = 0.01 g 1 milligram (mg) = 0.001 g |
1 kilolitre (kL) = 1,000 L
1 hectolitre (hL) = 100 L 1 dekalitre (daL) = 10 L 1 litre (L) = 1 L 1 decilitre (dL) = 0.1 L 1 centilitre (cL) = 0.01 L 1 millilitre (mL) = 0.001 L |
| 1 metre = 100 centimetres
1 metre = 1,000 millimetres |
1 gram = 100 centigrams
1 gram = 1,000 milligrams |
1 litre = 100 centilitre s
1 litre = 1,000 millilitre s |
To make conversions in the metric system, we will use the same technique we did in the Imperial system. Using the identity property of multiplication, we will multiply by a conversion factor of one to get to the correct units.
Have you ever run a 5K or 10K race? The length of those races are measured in kilometres. The metric system is commonly used in Canada when talking about the length of a race.
EXAMPLE 7
Nick ran a 10K race. How many metres did he run?
We will convert kilometres to metres using the identity property of multiplication.
| 10 kilometres | |
| Multiply the measurement to be converted by 1. | 10 kilometres × 1 |
| Write 1 as a fraction relating kilometres and metres. | |
| Simplify. | |
| Multiply. | 10,000 metres |
| Nick ran 10,000 metres. |
TRY IT 7.1
Sandy completed her first 5K race! How many metres did she run?
Show answer
5,000 metres
TRY IT 7.2
Herman bought a rug 2.5 metres in length. How many centimetres is the length?
Show answer
250 centimetres
EXAMPLE 8
Eleanor’s newborn baby weighed 3,200 grams. How many kilograms did the baby weigh?
We will convert grams into kilograms.
 |
|
| Multiply the measurement to be converted by 1. |  |
| Write 1 as a function relating kilograms and grams. | 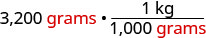 |
| Simplify. | 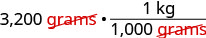 |
| Multiply. | |
| Divide. | 3.2 kilograms The baby weighed 3.2 kilograms. |
TRY IT 8.1
Kari’s newborn baby weighed 2,800 grams. How many kilograms did the baby weigh?
Show answer
2.8 kilograms
TRY IT 8.2
Anderson received a package that was marked 4,500 grams. How many kilograms did this package weigh?
Show answer
4.5 kilograms
As you become familiar with the metric system you may see a pattern. Since the system is based on multiples of ten, the calculations involve multiplying by multiples of ten. We have learned how to simplify these calculations by just moving the decimal.
To multiply by 10, 100, or 1,000, we move the decimal to the right one, two, or three places, respectively. To multiply by 0.1, 0.01, or 0.001, we move the decimal to the left one, two, or three places, respectively.
We can apply this pattern when we make measurement conversions in the metric system. In Example 8, we changed 3,200 grams to kilograms by multiplying by ![]() (or 0.001). This is the same as moving the decimal three places to the left.
(or 0.001). This is the same as moving the decimal three places to the left.
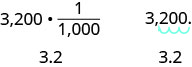
EXAMPLE 9
Convert a) 350 L to kilolitres b) 4.1 L to millilitre s.
- We will convert litres to kilolitres. In the Metric System of Measurement table, we see that
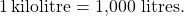
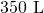
Multiply by 1, writing 1 as a fraction relating litres to kilolitres. 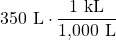
Simplify. 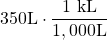
Move the decimal 3 units to the left. 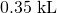
- We will convert litres to millilitre s. From Metric System of Measurement table we see that
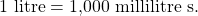

Multiply by 1, writing 1 as a fraction relating litres to millilitre s. 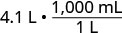
Simplify. 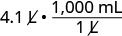
Move the decimal 3 units to the right. 

TRY IT 9.1
Convert: a) 725 L to kilolitres b) 6.3 L to millilitre s
Show answer
a) 7,250 kilolitres b) 6,300 millilitre s
TRY IT 9.2
Convert: a) 350 hL to litres b) 4.1 L to centilitre s
Show answer
a) 35,000 litres b) 410 centilitre s
Use Mixed Units of Measurement in the Imperial System
Performing arithmetic operations on measurements with mixed units of measures in the imperial system requires the same care we used in the Canadian system. Make sure to add or subtract like units.
EXAMPLE 10
Ryland is 1.6 metres tall. His younger brother is 85 centimetres tall. How much taller is Ryland than his younger brother?
We can convert both measurements to either centimetres or metres. Since metres is the larger unit, we will subtract the lengths in metres. We convert 85 centimetres to metres by moving the decimal 2 places to the left.
| Write the 85 centimetres as metres. |  |
Ryland is 0.75 m taller than his brother.
TRY IT 10.1
Mariella is 1.58 metres tall. Her daughter is 75 centimetres tall. How much taller is Mariella than her daughter? Write the answer in centimetres.
Show answer
83 centimetres
TRY IT 10.2
The fence around Hank’s yard is 2 metres high. Hank is 96 centimetres tall. How much shorter than the fence is Hank? Write the answer in metres.
Show answer
1.04 metres
EXAMPLE 11
Dena’s recipe for lentil soup calls for 150 millilitre s of olive oil. Dena wants to triple the recipe. How many litres of olive oil will she need?
We will find the amount of olive oil in millileters then convert to litres.
| Triple 150 mL | |
| Translate to algebra. | |
| Multiply. | 450 mL |
| Convert to litres. | |
| Simplify. | 0.45 L |
| Dena needs 0.45 litres of olive oil. |
TRY IT 11.1
A recipe for Alfredo sauce calls for 250 millilitre s of milk. Renata is making pasta with Alfredo sauce for a big party and needs to multiply the recipe amounts by 8. How many litres of milk will she need?
Show answer
2 litres
TRY IT 11.2
To make one pan of baklava, Dorothea needs 400 grams of filo pastry. If Dorothea plans to make 6 pans of baklava, how many kilograms of filo pastry will she need?
Show answer
2.4 kilograms
Convert Between the Imperial and the Metric Systems of Measurement
Many measurements in Canada are made in metric units. Our soda may come in 2-litre bottles, our calcium may come in 500-mg capsules, and we may run a 5K race. To work easily in both systems, we need to be able to convert between the two systems.
The table below shows some of the most common conversions.
| Length | Mass | Capacity |
|---|---|---|
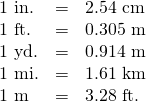 |
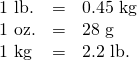 |
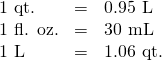 |
(Figure.2) shows how inches and centimetres are related on a ruler.

(Figure.3) shows the ounce and millilitre markings on a measuring cup.
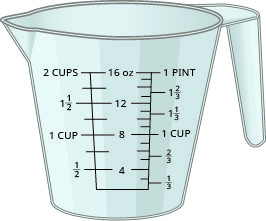
(Figure.4) shows how pounds and kilograms marked on a bathroom scale.

We make conversions between the systems just as we do within the systems—by multiplying by unit conversion factors.
EXAMPLE 12
Lee’s water bottle holds 500 mL of water. How many ounces are in the bottle? Round to the nearest tenth of an ounce.
| 500 mL | |
| Multiply by a unit conversion factor relating mL and ounces. | |
| Simplify. | |
| Divide. | 16.7 ounces. |
| The water bottle has 16.7 ounces. |
TRY IT 12.1
How many quarts of soda are in a 2-L bottle?
Show answer
2.12 quarts
TRY IT 12.2
How many litres are in 4 quarts of milk?
Show answer
3.8 litres
EXAMPLE 13
Soleil was on a road trip and saw a sign that said the next rest stop was in 100 kilometres. How many miles until the next rest stop?
| 100 kilometres | |
| Multiply by a unit conversion factor relating km and mi. | |
| Simplify. | |
| Divide. | 62 ounces. |
| Soleil will travel 62 miles. |
TRY IT 13.1
The height of Mount Kilimanjaro is 5,895 metres. Convert the height to feet.
Show answer
19,335.6 feet
TRY IT 13.2
The flight distance from Toronto to Vancouver is 3,364 kilometres. Convert the distance to miles.
Show answer
2,090 miles
Convert between Fahrenheit and Celsius Temperatures
Have you ever been in a foreign country and heard the weather forecast? If the forecast is for ![]() °F what does that mean?
°F what does that mean?
The Canadian and imperial systems use different scales to measure temperature. The Canadian system uses degrees Celsius, written °C. The imperial system uses degrees Fahrenheit, written°F. (Figure.5) shows the relationship between the two systems.
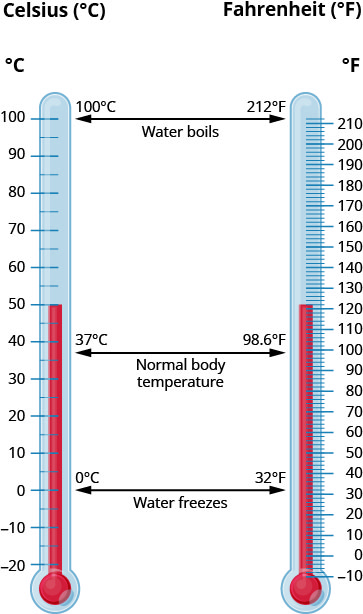
Temperature Conversion
To convert from Fahrenheit temperature, F, to Celsius temperature, C, use the formula
![]() .
.
To convert from Celsius temperature, C, to Fahrenheit temperature, F, use the formula
![]() .
.
EXAMPLE 14
Convert 50° Fahrenheit into degrees Celsius.
Solution
We will substitute 50°F into the formula to find C.
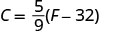 |
|
 |
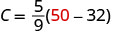 |
| Simplify in parentheses. | 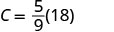 |
| Multiply. |  |
| So we found that 50°F is equivalent to 10°C. |
TRY IT 14.1
Convert the Fahrenheit temperature to degrees Celsius: 59° Fahrenheit.
Show answer
15°C
TRY IT 14.2
Convert the Fahrenheit temperature to degrees Celsius: 41° Fahrenheit.
Show answer
5°C
EXAMPLE 15
While visiting Paris, Woody saw the temperature was 20° Celsius. Convert the temperature into degrees Fahrenheit.
Solution
We will substitute 20°C into the formula to find F.
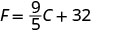 |
|
 |
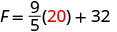 |
| Multiply. | 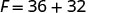 |
| Add. |  |
| So we found that 20°C is equivalent to 68°F. |
TRY IT 15.1
Convert the Celsius temperature to degrees Fahrenheit: the temperature in Helsinki, Finland, was 15° Celsius.
Show answer
59°F
TRY IT 15.2
Convert the Celsius temperature to degrees Fahrenheit: the temperature in Sydney, Australia, was 10° Celsius.
Show answer
50° F
Key Concepts
- Metric System of Measurement
- Length

- Mass

- Capacity

- Length
- Temperature Conversion
- To convert from Fahrenheit temperature, F, to Celsius temperature, C, use the formula
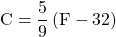
- To convert from Celsius temperature, C, to Fahrenheit temperature, F, use the formula
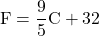
- To convert from Fahrenheit temperature, F, to Celsius temperature, C, use the formula
Practice Makes Perfect
Make Unit Conversions in the Imperial System
In the following exercises, convert the units.
| 1. A park bench is 6 feet long. Convert the length to inches. | 2. A floor tile is 2 feet wide. Convert the width to inches. |
| 3. A ribbon is 18 inches long. Convert the length to feet. | 4. Carson is 45 inches tall. Convert his height to feet. |
| 5. A football field is 160 feet wide. Convert the width to yards. | 6. On a baseball diamond, the distance from home plate to first base is 30 yards. Convert the distance to feet. |
| 7. Ulises lives 1.5 miles from school. Convert the distance to feet. | 8. Denver, Colorado, is 5,183 feet above sea level. Convert the height to miles. |
| 9. A killer whale weighs 4.6 tons. Convert the weight to pounds. | 10. Blue whales can weigh as much as 150 tons. Convert the weight to pounds. |
| 11. An empty bus weighs 35,000 pounds. Convert the weight to tons. | 12. At take-off, an airplane weighs 220,000 pounds. Convert the weight to tons. |
| 13. Rocco waited |
14. Misty’s surgery lasted |
| 15. How many teaspoons are in a pint? | 16. How many tablespoons are in a gallon? |
| 17. JJ’s cat, Posy, weighs 14 pounds. Convert her weight to ounces. | 18. April’s dog, Beans, weighs 8 pounds. Convert his weight to ounces. |
| 19. Crista will serve 20 cups of juice at her son’s party. Convert the volume to gallons. | 20. Lance needs 50 cups of water for the runners in a race. Convert the volume to gallons. |
| 21. Jon is 6 feet 4 inches tall. Convert his height to inches. | 22. Faye is 4 feet 10 inches tall. Convert her height to inches. |
| 23. The voyage of the Mayflower took 2 months and 5 days. Convert the time to days. | 24. Lynn’s cruise lasted 6 days and 18 hours. Convert the time to hours. |
| 25. Baby Preston weighed 7 pounds 3 ounces at birth. Convert his weight to ounces. | 26. Baby Audrey weighted 6 pounds 15 ounces at birth. Convert her weight to ounces. |
Use Mixed Units of Measurement in the Imperial System
In the following exercises, solve.
| 27. Eli caught three fish. The weights of the fish were 2 pounds 4 ounces, 1 pound 11 ounces, and 4 pounds 14 ounces. What was the total weight of the three fish? | 28. Judy bought 1 pound 6 ounces of almonds, 2 pounds 3 ounces of walnuts, and 8 ounces of cashews. How many pounds of nuts did Judy buy? |
| 29. One day Anya kept track of the number of minutes she spent driving. She recorded 45, 10, 8, 65, 20, and 35. How many hours did Anya spend driving? | 30. Last year Eric went on 6 business trips. The number of days of each was 5, 2, 8, 12, 6, and 3. How many weeks did Eric spend on business trips last year? |
| 31. Renee attached a 6 feet 6 inch extension cord to her computer’s 3 feet 8 inch power cord. What was the total length of the cords? | 32. Fawzi’s SUV is 6 feet 4 inches tall. If he puts a 2 feet 10 inch box on top of his SUV, what is the total height of the SUV and the box? |
| 33. Leilani wants to make 8 placemats. For each placemat she needs 18 inches of fabric. How many yards of fabric will she need for the 8 placemats? | 34. Mireille needs to cut 24 inches of ribbon for each of the 12 girls in her dance class. How many yards of ribbon will she need altogether? |
Make Unit Conversions in the Metric System
In the following exercises, convert the units.
| 35. Ghalib ran 5 kilometres. Convert the length to metres. | 36. Kitaka hiked 8 kilometres. Convert the length to metres. |
| 37. Estrella is 1.55 metres tall. Convert her height to centimetres. | 38. The width of the wading pool is 2.45 metres. Convert the width to centimetres. |
| 39. Mount Whitney is 3,072 metres tall. Convert the height to kilometres. | 40. The depth of the Mariana Trench is 10,911 metres. Convert the depth to kilometres. |
| 41. June’s multivitamin contains 1,500 milligrams of calcium. Convert this to grams. | 42. A typical ruby-throated hummingbird weights 3 grams. Convert this to milligrams. |
| 43. One stick of butter contains 91.6 grams of fat. Convert this to milligrams. | 44. One serving of gourmet ice cream has 25 grams of fat. Convert this to milligrams. |
| 45. The maximum mass of an airmail letter is 2 kilograms. Convert this to grams. | 46. Dimitri’s daughter weighed 3.8 kilograms at birth. Convert this to grams. |
| 47. A bottle of wine contained 750 millilitre s. Convert this to litres. | 48. A bottle of medicine contained 300 millilitre s. Convert this to litres. |
Use Mixed Units of Measurement in the Metric System
In the following exercises, solve.
| 49. Matthias is 1.8 metres tall. His son is 89 centimetres tall. How much taller is Matthias than his son? | 50. Stavros is 1.6 metres tall. His sister is 95 centimetres tall. How much taller is Stavros than his sister? |
| 51. A typical dove weighs 345 grams. A typical duck weighs 1.2 kilograms. What is the difference, in grams, of the weights of a duck and a dove? | 52. Concetta had a 2-kilogram bag of flour. She used 180 grams of flour to make biscotti. How many kilograms of flour are left in the bag? |
| 53. Harry mailed 5 packages that weighed 420 grams each. What was the total weight of the packages in kilograms? | 54. One glass of orange juice provides 560 milligrams of potassium. Linda drinks one glass of orange juice every morning. How many grams of potassium does Linda get from her orange juice in 30 days? |
| 55. Jonas drinks 200 millilitre s of water 8 times a day. How many litres of water does Jonas drink in a day? | 56. One serving of whole grain sandwich bread provides 6 grams of protein. How many milligrams of protein are provided by 7 servings of whole grain sandwich bread? |
Convert Between the Imperial and the Metric Systems of Measurement
In the following exercises, make the unit conversions. Round to the nearest tenth.
| 57. Bill is 75 inches tall. Convert his height to centimetres. | 58. Frankie is 42 inches tall. Convert his height to centimetres. |
| 59. Marcus passed a football 24 yards. Convert the pass length to metres | 60. Connie bought 9 yards of fabric to make drapes. Convert the fabric length to metres. |
| 61. According to research conducted by the CRC, Canadians regrettably produce more garbage per capita than any other country on earth, at 2,172.6 pounds per person annually. Convert the waste to kilograms. | 62. An average Canadian will throw away 163,000 pounds of trash over his or her lifetime. Convert this weight to kilograms. |
| 63. A 5K run is 5 kilometres long. Convert this length to miles. | 64. Kathryn is 1.6 metres tall. Convert her height to feet. |
| 65. Dawn’s suitcase weighed 20 kilograms. Convert the weight to pounds. | 66. Jackson’s backpack weighed 15 kilograms. Convert the weight to pounds. |
| 67. Ozzie put 14 gallons of gas in his truck. Convert the volume to litres. | 68. Bernard bought 8 gallons of paint. Convert the volume to litres. |
Convert between Fahrenheit and Celsius Temperatures
In the following exercises, convert the Fahrenheit temperatures to degrees Celsius. Round to the nearest tenth.
| 69. 86° Fahrenheit | 70. 77° Fahrenheit |
| 71. 104° Fahrenheit | 72. 14° Fahrenheit |
| 73. 72° Fahrenheit | 74. 4° Fahrenheit |
| 75. 0° Fahrenheit | 76. 120° Fahrenheit |
In the following exercises, convert the Celsius temperatures to degrees Fahrenheit. Round to the nearest tenth.
| 77. 5° Celsius | 78. 25° Celsius |
| 79. -10° Celsius | 80. -15° Celsius |
| 81. 22° Celsius | 82. 8° Celsius |
| 83. 43° Celsius | 84. 16° Celsius |
Everyday Math
| 85. Nutrition Julian drinks one can of soda every day. Each can of soda contains 40 grams of sugar. How many kilograms of sugar does Julian get from soda in 1 year? | 86. Reflectors The reflectors in each lane-marking stripe on a highway are spaced 16 yards apart. How many reflectors are needed for a one mile long lane-marking stripe? |
Writing Exercises
|
87. Some people think that 65° to 75° Fahrenheit is the ideal temperature range. a) What is your ideal temperature range? Why do you think so? b) Convert your ideal temperatures from Fahrenheit to Celsius. |
88.
a) Did you grow up using the Canadian. or the Imperial system of measurement? b) Describe two examples in your life when you had to convert between the two systems of measurement. |
Answers
| 1. 72 inches | 3. 1.5 feet | 5. |
| 7. 7,920 feet | 9. 9,200 pounds | 11. |
| 13. 5,400 s | 15. |
17. |
| 19. |
21. 76 in. | 23. 65 days |
| 25. 115 ounces | 27. 8 lbs. 13 oz. | 29. 3.05 hours |
| 31. 10 ft. 2 in. | 33. 4 yards | 35. 5,000 metres |
| 37. 155 centimetres | 39. 3.072 kilometres | 41. 1.5 grams |
| 43. 91,600 milligrams | 45. 2,000 grams | 47. 0.75 litres |
| 49. 91 centimetres | 49. 91 centimetres | 49. 91 centimetres |
| 53. 2.1 kilograms | 55. 1.6 litres | 57. 190.5 centimetres |
| 59. 21.9 metres | 61. 985.5 kilograms | 63. 3.1 miles |
| 65. 44 pounds | 67. 53.2 litres | 69. 30°C |
| 71. 40°C | 73. 22.2°C | 75. -17.8°C |
| 77. 41°F | 79. 14°F | 81. 71.6°F |
| 83. 109.4°F | 85. 14.6 kilograms | 87. Answers may vary. |
Attributions
This chapter has been adapted from “Systems of Measurement” in Elementary Algebra (OpenStax) by Lynn Marecek and MaryAnne Anthony-Smith, which is under a CC BY 4.0 Licence. Adapted by Izabela Mazur. See the Copyright page for more information.

