CHAPTER 7 Powers, Roots, and Scientific Notation
7.3 Integer Exponents and Scientific Notation
Learning Objectives
By the end of this section, you will be able to:
- Use the definition of a negative exponent
- Simplify expressions with integer exponents
- Convert from decimal notation to scientific notation
- Convert scientific notation to decimal form
- Multiply and divide using scientific notation
Use the Definition of a Negative Exponent
We saw that the Quotient Property for Exponents introduced earlier in this chapter, has two forms depending on whether the exponent is larger in the numerator or the denominator.
Quotient Property for Exponents
If ![]() is a real number,
is a real number, ![]() , and
, and ![]() are whole numbers, then
are whole numbers, then
What if we just subtract exponents regardless of which is larger?
Let’s consider ![]() .
.
We subtract the exponent in the denominator from the exponent in the numerator.
We can also simplify ![]() by dividing out common factors:
by dividing out common factors:
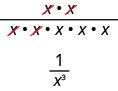
This implies that ![]() and it leads us to the definition of a negative exponent.
and it leads us to the definition of a negative exponent.
Negative Exponent
If ![]() is an integer and
is an integer and ![]() , then
, then ![]() .
.
The negative exponent tells us we can re-write the expression by taking the reciprocal of the base and then changing the sign of the exponent.
Any expression that has negative exponents is not considered to be in simplest form. We will use the definition of a negative exponent and other properties of exponents to write the expression with only positive exponents.
For example, if after simplifying an expression we end up with the expression ![]() , we will take one more step and write
, we will take one more step and write ![]() . The answer is considered to be in simplest form when it has only positive exponents.
. The answer is considered to be in simplest form when it has only positive exponents.
EXAMPLE 1
Simplify: a) ![]() b)
b) ![]() .
.
| a) | |
| Use the definition of a negative exponent, |
|
| Simplify. | |
| b) | |
| Use the definition of a negative exponent, |
|
| Simplify. |
TRY IT 1.1
Simplify: a) ![]() b)
b) ![]() .
.
Show answer
a) ![]() b)
b) ![]()
TRY IT 1.2
Simplify: a) ![]() b)
b) ![]() .
.
Show answer
a) ![]() b)
b) ![]()
In (Example 1) we raised an integer to a negative exponent. What happens when we raise a fraction to a negative exponent? We’ll start by looking at what happens to a fraction whose numerator is one and whose denominator is an integer raised to a negative exponent.
| Use the definition of a negative exponent, |
|
| Simplify the complex fraction. | |
| Multiply. |
This leads to the Property of Negative Exponents.
Property of Negative Exponents
If ![]() is an integer and
is an integer and ![]() , then
, then ![]() .
.
EXAMPLE 2
Simplify: a) ![]() b)
b) ![]() .
.
| a) | |
| Use the property of a negative exponent, |
|
| b) | |
| Use the property of a negative exponent, |
|
| Simplify. |
TRY IT 2.1
Simplify: a) ![]() b)
b) ![]() .
.
Show answer
a) ![]() b)
b) ![]()
TRY IT 2.2
Simplify: a) ![]() b)
b) ![]() .
.
Show answer
a) ![]() b)
b) ![]()
Suppose now we have a fraction raised to a negative exponent. Let’s use our definition of negative exponents to lead us to a new property.
| Use the definition of a negative exponent, |
|
| Simplify the denominator. | |
| Simplify the complex fraction. | |
| But we know that |
|
| This tells us that: |
To get from the original fraction raised to a negative exponent to the final result, we took the reciprocal of the base—the fraction—and changed the sign of the exponent.
This leads us to the Quotient to a Negative Power Property.
Quotient to a Negative Exponent Property
If ![]() are real numbers,
are real numbers, ![]() , and
, and ![]() is an integer, then
is an integer, then ![]() .
.
EXAMPLE 3
Simplify: a) ![]() b)
b) ![]() .
.
| a) | |
| Use the Quotient to a Negative Exponent Property, |
|
| Take the reciprocal of the fraction and change the sign of the exponent. | |
| Simplify. | |
| b) | |
| Use the Quotient to a Negative Exponent Property, |
|
| Take the reciprocal of the fraction and change the sign of the exponent. | |
| Simplify. |
TRY IT 3.1
Simplify: a) ![]() b)
b) ![]() .
.
Show answer
a) ![]() b)
b) ![]()
TRY IT 3.2
Simplify: a) ![]() b)
b) ![]() .
.
Show answer
a) ![]() b)
b) ![]()
When simplifying an expression with exponents, we must be careful to correctly identify the base.
EXAMPLE 4
Simplify: a) ![]() b)
b) ![]() c)
c) ![]() d)
d) ![]() .
.
| a) Here the exponent applies to the base |
|
| Take the reciprocal of the base and change the sign of the exponent. | |
| Simplify. | |
| b) The expression |
|
| Rewrite as a product with |
|
| Take the reciprocal of the base and change the sign of the exponent. | |
| Simplify. | |
| c) Here the exponent applies to the base |
|
| Take the reciprocal of the base and change the sign of the exponent. | |
| Simplify. | |
| d) The expression |
|
| Rewrite as a product with |
|
| Take the reciprocal of the base and change the sign of the exponent. | |
| Simplify. |
TRY IT 4.1
Simplify: a) ![]() b)
b) ![]() c)
c) ![]() d)
d) ![]() .
.
Show answer
a) ![]() b)
b) ![]() c) 25 d)
c) 25 d) ![]()
TRY IT 4.2
Simplify: a) ![]() b)
b) ![]() , c)
, c) ![]() d)
d) ![]() .
.
Show answer
a) ![]() b)
b) ![]() c) 49 d)
c) 49 d) ![]()
We must be careful to follow the Order of Operations. In the next example, parts (a) and (b) look similar, but the results are different.
EXAMPLE 5
Simplify: a) ![]() b)
b) ![]() .
.
| a) Do exponents before multiplication. |
|
| Use |
|
| Simplify. | |
| b) | |
| Simplify inside the parentheses first. | |
| Use |
|
| Simplify. |
TRY IT 5.1
Simplify: a) ![]() b)
b) ![]() .
.
Show answer
a) ![]() b)
b) ![]()
TRY IT 5.2
Simplify: a) ![]() b)
b) ![]() .
.
Show answer
a) 2 b) ![]()
When a variable is raised to a negative exponent, we apply the definition the same way we did with numbers. We will assume all variables are non-zero.
EXAMPLE 6
Simplify: a) ![]() b)
b) ![]() .
.
| a) | |
| Use the definition of a negative exponent |
|
| b) | |
| Use the definition of a negative exponent |
|
| Simplify. |
TRY IT 6.1
Simplify: a) ![]() b)
b) ![]() .
.
Show answer
a) ![]() b)
b) ![]()
TRY IT 6.2
Simplify: a) ![]() b)
b) ![]() .
.
Show answer
a) ![]() b)
b) ![]()
When there is a product and an exponent we have to be careful to apply the exponent to the correct quantity. According to the Order of Operations, we simplify expressions in parentheses before applying exponents. We’ll see how this works in the next example.
EXAMPLE 7
Simplify: a) ![]() b)
b) ![]() c)
c) ![]() .
.
| a) Notice the exponent applies to just the base. | |
| Take the reciprocal of |
|
| Simplify. | |
| b) Her the parentheses make the exponent apply to the base. | |
| Take the reciprocal of |
|
| Simplify. | |
| c) The base here is |
|
| Take the reciprocal of |
|
| Simplify. | |
| Use |
TRY IT 7.1
Simplify: a) ![]() b)
b) ![]() c)
c) ![]() .
.
Show answer
a) ![]() b)
b) ![]() c)
c) ![]()
TRY IT 7.2
Simplify: a) ![]() b)
b) ![]()
![]() c)
c) ![]() .
.
Show answer
a) ![]() b)
b) ![]()
![]() c)
c) ![]()
With negative exponents, the Quotient Rule needs only one form ![]() , for
, for ![]() . When the exponent in the denominator is larger than the exponent in the numerator, the exponent of the quotient will be negative.
. When the exponent in the denominator is larger than the exponent in the numerator, the exponent of the quotient will be negative.
Simplify Expressions with Integer Exponents
All of the exponent properties we developed earlier in the chapter with whole number exponents apply to integer exponents, too. We restate them here for reference.
Summary of Exponent Properties
If ![]() are real numbers, and
are real numbers, and ![]() are integers, then
are integers, then
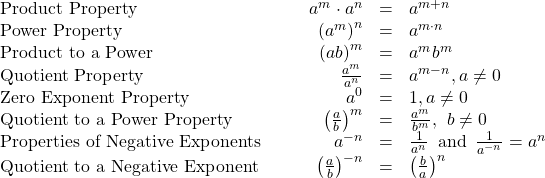
EXAMPLE 8
Simplify: a) ![]() b)
b) ![]() c)
c) ![]() .
.
-
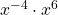
Use the Product Property, 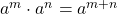 .
.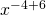
Simplify 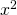
-
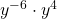
Notice the same bases, so add the exponents. 
Simplify. 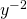
Use the definition of a negative exponent, 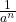 .
.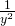
-
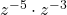
Add the exponents, since the bases are the same. 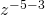
Simplify. 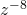
Take the reciprocal and change the sign of the exponent, using the definition of a negative exponent. 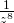
TRY IT 8.1
Simplify: a) ![]() b)
b) ![]() c)
c) ![]() .
.
Show answer
a) ![]() b)
b) ![]() c)
c) ![]()
TRY IT 8.2
Simplify: a) ![]() b)
b) ![]() c)
c) ![]() .
.
Show answer
a) ![]() b)
b) ![]() c)
c) ![]()
In the next two examples, we’ll start by using the Commutative Property to group the same variables together. This makes it easier to identify the like bases before using the Product Property.
EXAMPLE 9
Simplify: ![]() .
.
| Use the Commutative Property to get like bases together. | |
| Add the exponents for each base. | |
| Take the reciprocals and change the signs of the exponents. | |
| Simplify. |
TRY IT 9.1
Simplify: ![]() .
.
Show answer
![]()
TRY IT 9.2
Simplify: ![]() .
.
Show answer
![]()
If the monomials have numerical coefficients, we multiply the coefficients, just like we did earlier.
EXAMPLE 10
Simplify: ![]() .
.
| Rewrite with the like bases together. | |
| Multiply the coefficients and add the exponents of each variable. | |
| Use the definition of a negative exponent, |
|
| Simplify. |
TRY IT 10.1
Simplify: ![]() .
.
Show answer
![]()
TRY IT 10.2
Simplify: ![]() .
.
Show answer
![]()
In the next two examples, we’ll use the Power Property and the Product to a Power Property.
EXAMPLE 11
Simplify: ![]() .
.
| Use the product to a Power Property, |
|
| Use the Power Property, |
|
| Use the Definition of a Negative Exponent, |
|
| Simplify. |
|
TRY IT 11.1
Simplify: ![]() .
.
Show answer
![]()
TRY IT 11.2
Simplify: ![]() .
.
Show answer
![]()
EXAMPLE 12
Simplify: ![]() .
.
| Use the Product to a Power Property, |
|
| Simplify and multiply the exponents of |
|
| Rewrite by using the Definition of a Negative Exponent, |
|
| Simplify. |
TRY IT 12.1
Simplify: ![]() .
.
Show answer
![]()
TRY IT 12.2
Simplify: ![]() .
.
Show answer
![]()
EXAMPLE 13
Simplify: ![]() .
.
| Use the Quotient Property, |
|
| Simplify. |
|
TRY IT 13.1
Simplify: ![]() .
.
Show answer
![]()
TRY IT 13.2
Simplify: ![]() .
.
Show answer
![]()
Convert from Decimal Notation to Scientific Notation
Remember working with place value for whole numbers and decimals? Our number system is based on powers of 10. We use tens, hundreds, thousands, and so on. Our decimal numbers are also based on powers of tens—tenths, hundredths, thousandths, and so on. Consider the numbers 4,000 and ![]() . We know that 4,000 means
. We know that 4,000 means ![]() and 0.004 means
and 0.004 means ![]() .
.
If we write the 1000 as a power of ten in exponential form, we can rewrite these numbers in this way:

When a number is written as a product of two numbers, where the first factor is a number greater than or equal to one but less than 10, and the second factor is a power of 10 written in exponential form, it is said to be in scientific notation.
Scientific Notation
A number is expressed in scientific notation when it is of the form
It is customary in scientific notation to use as the ![]() multiplication sign, even though we avoid using this sign elsewhere in algebra.
multiplication sign, even though we avoid using this sign elsewhere in algebra.
If we look at what happened to the decimal point, we can see a method to easily convert from decimal notation to scientific notation.

In both cases, the decimal was moved 3 places to get the first factor between 1 and 10
![]()
EXAMPLE 14
Write in scientific notation: 37,000.




TRY IT 14.1
Write in scientific notation: ![]() .
.
Show answer
![]()
TRY IT 14.2
Write in scientific notation: ![]() .
.
Show answer
![]()
- Move the decimal point so that the first factor is greater than or equal to 1 but less than 10.
- Count the number of decimal places, n, that the decimal point was moved.
- Write the number as a product with a power of 10.
If the original number is:- greater than 1, the power of 10 will be 10n.
- between 0 and 1, the power of 10 will be 10−n.
- Check.
EXAMPLE 15
Write in scientific notation: ![]() .
.
The original number, ![]() , is between 0 and 1 so we will have a negative power of 10
, is between 0 and 1 so we will have a negative power of 10
| Move the decimal point to get 5.2, a number between 1 and 10. | |
| Count the number of decimal places the point was moved. | |
| Write as a product with a power of 10. | |
| Check. | |
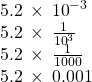 |
|
TRY IT 15.1
Write in scientific notation: ![]() .
.
Show answer
![]()
TRY IT 15.2
Write in scientific notation: ![]() .
.
Show answer
![]()
Convert Scientific Notation to Decimal Form
How can we convert from scientific notation to decimal form? Let’s look at two numbers written in scientific notation and see.

If we look at the location of the decimal point, we can see an easy method to convert a number from scientific notation to decimal form.
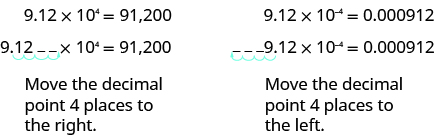
In both cases the decimal point moved 4 places. When the exponent was positive, the decimal moved to the right. When the exponent was negative, the decimal point moved to the left.
EXAMPLE 16
Convert to decimal form: ![]() .
.



TRY IT 16.1
Convert to decimal form: ![]() .
.
Show answer
1,300
TRY IT 16.2
Convert to decimal form: ![]() .
.
Show answer
92,500
The steps are summarized below.
To convert scientific notation to decimal form:
- Determine the exponent,
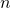 , on the factor 10.
, on the factor 10. - Move the decimal
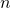 places, adding zeros if needed.
places, adding zeros if needed.
- If the exponent is positive, move the decimal point
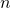 places to the right.
places to the right. - If the exponent is negative, move the decimal point
 places to the left.
places to the left.
- If the exponent is positive, move the decimal point
- Check.
EXAMPLE 17
Convert to decimal form: ![]() .
.
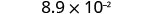 |
|
| Determine the exponent, n, on the factor 10. |  |
| Since the exponent is negative, move the decimal point 2 places to the left. | 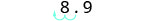 |
| Add zeros as needed for placeholders. | 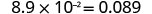 |
TRY IT 17.1
Convert to decimal form: ![]() .
.
Show answer
0.00012
TRY IT 17.2
Convert to decimal form: ![]() .
.
Show answer
0.075
Multiply and Divide Using Scientific Notation
Astronomers use very large numbers to describe distances in the universe and ages of stars and planets. Chemists use very small numbers to describe the size of an atom or the charge on an electron. When scientists perform calculations with very large or very small numbers, they use scientific notation. Scientific notation provides a way for the calculations to be done without writing a lot of zeros. We will see how the Properties of Exponents are used to multiply and divide numbers in scientific notation.
EXAMPLE 18
Multiply. Write answers in decimal form: ![]() .
.
| Use the Commutative Property to rearrange the factors. | |
| Multiply. | |
| Change to decimal form by moving the decimal two places left. |
TRY IT 18.1
Multiply ![]() . Write answers in decimal form.
. Write answers in decimal form.
Show answer
0.06
TRY IT 18.2
Multiply ![]() . Write answers in decimal form.
. Write answers in decimal form.
Show answer
0.009
EXAMPLE 19
Divide. Write answers in decimal form: ![]() .
.
| Separate the factors, rewriting as the product of two fractions. | |
| Divide. | |
| Change to decimal form by moving the decimal five places right. | |
TRY IT 19.1
Divide ![]() . Write answers in decimal form.
. Write answers in decimal form.
Show answer
400,000
TRY IT 19.2
Divide ![]() . Write answers in decimal form.
. Write answers in decimal form.
Show answer
20,000
Access these online resources for additional instruction and practice with integer exponents and scientific notation:
Key Concepts
- Property of Negative Exponents
- If
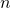 is a positive integer and
is a positive integer and 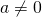 , then
, then 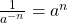
- If
- Quotient to a Negative Exponent
- If
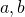 are real numbers,
are real numbers, 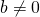 and
and 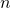 is an integer , then
is an integer , then 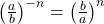
- If
- To convert a decimal to scientific notation:
- Move the decimal point so that the first factor is greater than or equal to 1 but less than 10.
- Count the number of decimal places,
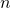 , that the decimal point was moved.
, that the decimal point was moved. - Write the number as a product with a power of 10. If the original number is:
- greater than 1, the power of 10 will be
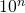
- between 0 and 1, the power of 10 will be
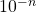
- greater than 1, the power of 10 will be
- Check.
- To convert scientific notation to decimal form:
- Determine the exponent,
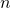 , on the factor 10.
, on the factor 10. - Move the decimal
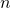 places, adding zeros if needed.
places, adding zeros if needed.
- If the exponent is positive, move the decimal point
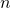 places to the right.
places to the right. - If the exponent is negative, move the decimal point
 places to the left.
places to the left.
- If the exponent is positive, move the decimal point
- Check
- Determine the exponent,
Practice Makes Perfect
Use the Definition of a Negative Exponent
In the following exercises, simplify.
|
1. a) |
2. a) |
|
3. a) |
4. a) |
|
5. a) |
6. a) |
|
7. a) |
8. a) |
|
9. a) |
10. a) |
|
11. a) |
12. a) |
|
13. a) |
14. a) |
|
15. a) |
16. a) |
|
17. a) |
18. a) |
|
19. a) |
20. a) |
|
21. a) |
22. a) |
|
23. a) |
24. a) |
|
25. a) |
26. a) |
|
27. a) |
28. a) |
Simplify Expressions with Integer Exponents
In the following exercises, simplify.
|
29. a) |
30.
a) |
|
31. a) |
32. a) |
| 33. |
34. |
| 35. |
36. |
| 37. |
38. |
| 39. |
40. |
| 41. |
42. |
| 43. |
44. |
| 45. |
46. |
| 47. |
48. |
| 49. |
Convert from Decimal Notation to Scientific Notation
In the following exercises, write each number in scientific notation.
| 50. 57,000 | 51. 340,000 |
| 52. 8,750,000 | 53. 1,290,000 |
| 54. 0.026 | 55. 0.041 |
| 56. 0.00000871 | 57. 0.00000103 |
Convert Scientific Notation to Decimal Form
In the following exercises, convert each number to decimal form.
| 58. |
59. |
| 60. |
61. |
| 62. |
63. |
| 64. |
65. |
Multiply and Divide Using Scientific Notation
In the following exercises, multiply. Write your answer in decimal form.
| 66. |
67. |
| 68. |
69. |
In the following exercises, divide. Write your answer in decimal form.
| 70. |
71. |
| 72. |
73. |
Everyday Math
| 74. The population of the United States on July 1, 2010 was about 34,000,000. Write the number in scientific notation. | 75. The population of the world on July 1, 2010 was more than 6,850,000,000. Write the number in scientific notation |
| 76. The average width of a human hair is 0.0018 centimetres. Write the number in scientific notation. | 77. The probability of winning the 2010 Megamillions lottery was about 0.0000000057. Write the number in scientific notation. |
| 78. In 2010, the number of Facebook users each day who changed their status to ‘engaged’ was |
79. At the start of 2012, the US federal budget had a deficit of more than |
| 80. The concentration of carbon dioxide in the atmosphere is |
81. The width of a proton is |
|
82. Health care costs The Centers for Medicare and Medicaid projects that American consumers will spend more than $4 trillion on health care by 2017
|
83. Coin production In 1942, the U.S. Mint produced 154,500,000 nickels. Write 154,500,000 in scientific notation. |
|
84. Distance The distance between Earth and one of the brightest stars in the night star is 33.7 light years. One light year is about 6,000,000,000,000 (6 trillion), miles. a) Write the number of miles in one light year in scientific notation. b)Use scientific notation to find the distance between Earth and the star in miles. Write the answer in scientific notation. |
85. Debt At the end of fiscal year 2019 the gross Canadian federal government debt was estimated to be approximately $685,450,000,000 ($685.45 billion), according to the Federal Budget. The population of Canada was approximately 37,590,000 people at the end of fiscal year 2019 a) Write the debt in scientific notation. b) Write the population in scientific notation. c) Find the amount of debt per person by using scientific notation to divide the debt by the population. Write the answer in scientific notation. |
Writing Exercises.
| 86.
a) Explain the meaning of the exponent in the expression b) Explain the meaning of the exponent in the expression |
87. When you convert a number from decimal notation to scientific notation, how do you know if the exponent will be positive or negative? |
Answers
| 1. a) |
3. a) |
5. a) |
| 7. a) |
9. a) |
11. a) |
| 13. a) |
15. a) |
17. a) |
| 19. a) |
21. a) |
23. a) |
| 25. a) |
27. a) |
29. a) |
| 31. a) 1 b) |
33. |
35. |
| 37. |
39. |
41. |
| 43. |
45. |
47. |
| 49. |
51. |
53. |
| 55. |
57. |
59. 830 |
| 61. 16,000,000,000 | 63. 0.038 | 65. 0.0000193 |
| 67. 0.02 | 69. |
71. 500,000,000 |
| 73. 20,000,000 | 75. |
77. |
| 79. 15,000,000,000,000 | 81. 0.00001 | 83. |
| 85. a) |
87. Answers will vary |
Attributions
This chapter has been adapted from “Integer Exponents and Scientific Notation” in Elementary Algebra (OpenStax) by Lynn Marecek and MaryAnne Anthony-Smith, which is under a CC BY 4.0 Licence. Adapted by Izabela Mazur. See the Copyright page for more information.

