1.5 Multiply and Divide Integers

Izabela Mazur

CHAPTER 1 Whole Numbers, Integers, and Introduction to Algebra

1.5 Multiply and Divide Integers

Learning Objectives

By the end of this section, you will be able to:

Multiply integers
Divide integers
Simplify expressions with integers
Evaluate variable expressions with integers
Translate English phrases to algebraic expressions
Use integers in applications

Multiply Integers

Since multiplication is mathematical shorthand for repeated addition, our model can easily be applied to show multiplication of integers. Let’s look at this concrete model to see what patterns we notice. We will use the same examples that we used for addition and subtraction. Here, we will use the model just to help us discover the pattern.

We remember that $a \cdot b$ means add a, b times. Here, we are using the model just to help us discover the pattern.

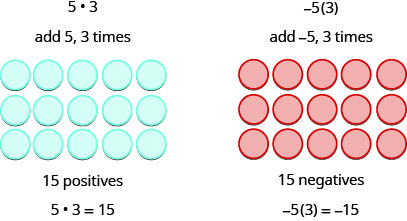
The next two examples are more interesting.

What does it mean to multiply 5 by $-3?$ It means subtract 5, 3 times. Looking at subtraction as “taking away,” it means to take away 5, 3 times. But there is nothing to take away, so we start by adding neutral pairs on the workspace. Then we take away 5 three times.

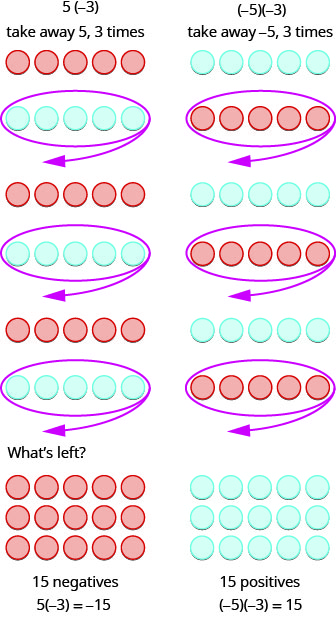
In summary:

$\begin{array}{cccccccc}\hfill 5 \cdot 3& =\hfill & 15\hfill & & & \hfill -5\left(3\right)& =\hfill & -15\hfill \\ \hfill 5\left(-3\right)& =\hfill & -15\hfill & & & \hfill \left(-5\right)\left(-3\right)& =\hfill & 15\hfill \end{array}$

Notice that for multiplication of two signed numbers, when the:

signs are the same, the product is positive.
signs are different, the product is negative.

We’ll put this all together in the chart below

Multiplication of Signed Numbers

For multiplication of two signed numbers:

Same signs

Product

Example

Two positives
Two negatives

Positive
Positive

$\begin{array}{ccc}\hfill 7\cdot4& =\hfill & 28\hfill \\ \hfill -8\left(-6\right)& =\hfill & 48\hfill \end{array}$

Different signs

Product

Example

Positive \cdot negative
Negative \cdot positive

Negative
Negative

$\begin{array}{ccc}\hfill 7\left(-9\right)& =\hfill & -63\hfill \\ \hfill -5\cdot10& =\hfill & -50\hfill \end{array}$

EXAMPLE 1

Multiply: a) $-9\cdot3$ b) $-2\left(-5\right)$ c) $4\left(-8\right)$ d) $7\cdot6$ .

Solution

a) Multiply, noting that the signs are different so the product is negative.	$\begin{array}{c}-9\cdot3\\ -27\end{array}$
b) Multiply, noting that the signs are the same so the product is positive.	$\begin{array}{c}-2\left(-5\right)\\ 10\end{array}$
c) Multiply, with different signs.	$\begin{array}{c}4\left(-8\right)\\ -32\end{array}$
d) Multiply, with same signs.	$\begin{array}{c}7\cdot6\\ 42\end{array}$

TRY IT 1.1

Multiply: a) $-6\cdot8$ b) $-4\left(-7\right)$ c) $9\left(-7\right)$ d) $5\cdot12$ .

Show answer

a) $-48$ b) 28 c) $-63$ d) 60

TRY IT 1.2

Multiply: a) $-8\cdot7$ b) $-6\left(-9\right)$ c) $7\left(-4\right)$ d) $3\cdot13$ .

Show answer

a) $-56$ b) 54 c) $-28$ d) 39

When we multiply a number by 1, the result is the same number. What happens when we multiply a number by $-1$ ? Let’s multiply a positive number and then a negative number by $-1$ to see what we get.

$\begin{array}{ccccccc}& & & \hfill -1\cdot 4\hfill & & & \hfill -1\left(-3\right)\hfill \\ \text{Multiply.}\hfill & & & \hfill -4\hfill & & & \hfill 3\hfill \\ & & & \hfill -4\phantom{\rule{0.2em}{0ex}}\text{is the opposite of}\phantom{\rule{0.2em}{0ex}}4.\hfill & & & \hfill 3\phantom{\rule{0.2em}{0ex}}\text{is the opposite of}\phantom{\rule{0.2em}{0ex}}-3.\hfill \end{array}$

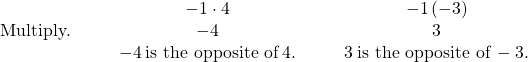
Each time we multiply a number by $-1$ , we get its opposite!

Multiplication by $-1$

$-1a=\text{-}a$

Multiplying a number by $-1$ gives its opposite.

EXAMPLE 2

Multiply: a) $-1\cdot7$ b) $-1\left(-11\right)$ .

Solution

a) Multiply, noting that the signs are different so the product is negative.	$\begin{array}{c}-1\cdot7\\ -7\\ -7\phantom{\rule{0.2em}{0ex}}\text{is the opposite of}\phantom{\rule{0.2em}{0ex}}7.\end{array}$
b) Multiply, noting that the signs are the same so the product is positive.	$\begin{array}{c}-1\left(-11\right)\\ 11\\ 11\phantom{\rule{0.2em}{0ex}}\text{is the opposite of}\phantom{\rule{0.2em}{0ex}}-11.\end{array}$

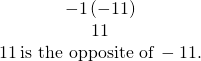TRY IT 2.1

Multiply: a) $-1\cdot9$ b) $-1 \cdot \left(-17\right)$ .

Show answer

a) $-9$ b) 17

TRY IT 2.2

Multiply: a) $-1\cdot8$ b) $-1 \cdot \left(-16\right)$ .

Show answer

a) $-8$ b) 16

Divide Integers

What about division? Division is the inverse operation of multiplication. So, $15\div 3=5$ because $5\cdot3=15$ . In words, this expression says that 15 can be divided into three groups of five each because adding five three times gives 15. Look at some examples of multiplying integers, to figure out the rules for dividing integers.

$\begin{array}{cccccccccccccc}\hfill 5\cdot3& =\hfill & 15\phantom{\rule{0.2em}{0ex}}\text{so}\phantom{\rule{0.2em}{0ex}}15\div 3\hfill & =\hfill & 5\hfill & & & & & \hfill -5\left(3\right)& =\hfill & -15\phantom{\rule{0.2em}{0ex}}\text{so}\phantom{\rule{0.2em}{0ex}}-15\div3\hfill & =\hfill & -5\hfill \\ \hfill \left(-5\right)\left(-3\right)& =\hfill & 15\phantom{\rule{0.2em}{0ex}}\text{so}\phantom{\rule{0.2em}{0ex}}15\div \left(-3\right)\hfill & =\hfill & -5\hfill & & & & & \hfill 5\left(-3\right)& =\hfill & -15\phantom{\rule{0.2em}{0ex}}\text{so}\phantom{\rule{0.2em}{0ex}}-15\div \left(-3\right)\hfill & =\hfill & 5\hfill \end{array}$

Division follows the same rules as multiplication!

For division of two signed numbers, when the:

signs are the same, the quotient is positive.
signs are different, the quotient is negative.

And remember that we can always check the answer of a division problem by multiplying.

Multiplication and Division of Signed Numbers

For multiplication and division of two signed numbers:

If the signs are the same, the result is positive.
If the signs are different, the result is negative.

Same signs	Result
Two positives	Positive
Two negatives	Positive

If the signs are the same, the result is positive.

Different signs	Result
Positive and negative	Negative
Negative and positive	Negative

If the signs are different, the result is negative.

EXAMPLE 3

Divide: a) $-27\div 3$ b) $-100\div \left(-4\right)$ .

Solution

a) Divide. With different signs, the quotient is negative.	$\begin{array}{c}-27\div 3\\ -9\end{array}$
b) Divide. With signs that are the same, the quotient is positive.	$\begin{array}{c}-100\div\left(-4\right)\\ 25\end{array}$

TRY IT 3.1

Divide: a) $-42\div 6$ b) $-117\div\left(-3\right)$ .

Show answer

a) $-7$ b) 39

TRY IT 3.2

Divide: a) $-63\div 7$ b) $-115\div\left(-5\right)$ .

Show answer

a) $-9$ b) 23

Simplify Expressions with Integers

What happens when there are more than two numbers in an expression? The order of operations still applies when negatives are included. Remember My Dear Aunt Sally?

Let’s try some examples. We’ll simplify expressions that use all four operations with integers—addition, subtraction, multiplication, and division. Remember to follow the order of operations.

EXAMPLE 4

Simplify: $7\left(-2\right)+4\left(-7\right)-6$ .

Solution

	$7\left(-2\right)+4\left(-7\right)-6$
Multiply first.	$-14+\left(-28\right)-6$
Add.	$-42-6$
Subtract.	$-48$

TRY IT 4.1

Simplify: $8\left(-3\right)+5\left(-7\right)-4$ .

Show answer

$-63$

TRY IT 4.2

Simplify: $9\left(-3\right)+7\left(-8\right)-1$ .

Show answer

$-84$

EXAMPLE 5

Simplify: a) ${\left(-2\right)}^{4}$ b) $\text{-}{2}^{4}$ .

Solution

a) Write in expanded form. Multiply. Multiply. Multiply.	$\begin{array}{c}{\left(-2\right)}^{4}\\ \left(-2\right)\left(-2\right)\left(-2\right)\left(-2\right)\\ 4\left(-2\right)\left(-2\right)\\ -8\left(-2\right)\\ 16\end{array}$
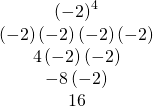b) Write in expanded form. We are asked to find the opposite of $\phantom{\rule{0.2em}{0ex}}{2}^{4}$ . Multiply. Multiply. Multiply.	$\begin{array}{c}\text{-}{2}^{4}\\ \text{-}\left(2\cdot2\cdot2\cdot2\right)\\ \text{-}\left(4\cdot2\cdot2\right)\\ \text{-}\left(8\cdot2\right)\\ 16\end{array}$

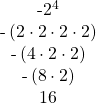Notice the difference in parts a) and b). In part a), the exponent means to raise what is in the parentheses, the $\left(-2\right)$ to the ${4}^{\text{th}}$ power. In part b), the exponent means to raise just the 2 to the ${4}^{\text{th}}$ power and then take the opposite.

TRY IT 5.1

Simplify: a) ${\left(-3\right)}^{4}$ b) $\text{-}{3}^{4}$ .

Show answer

a) 81 b) $-81$

TRY IT 5.2

Simplify: a) ${\left(-7\right)}^{2}$ b) $\text{-}{7}^{2}$ .

Show answer

a) 49 b) $-49$

The next example reminds us to simplify inside parentheses first.

EXAMPLE 6

Simplify: $12-3\left(9-12\right)$ .

Solution

	$12-3\left(9-12\right)$
Subtract in parentheses first.	$12-3\left(-3\right)$
Multiply.	$12-\left(-9\right)$
Subtract.	$21$

TRY IT 6.1

Simplify: $17-4\left(8-11\right)$ .

Show answer

29

TRY IT 6.2

Simplify: $16-6\left(7-13\right)$ .

Show answer

52

EXAMPLE 7

Simplify: $8\left(-9\right)\div{\left(-2\right)}^{3}$ .

Solution

	$8\left(-9\right)\div{\left(-2\right)}^{3}$
Exponents first.	$8\left(-9\right)\div\left(-8\right)$
Multiply.	$-72\div \left(-8\right)$
Divide.	$9$

TRY IT 7.1

Simplify: $12\left(-9\right)\div{\left(-3\right)}^{3}$ .

Show answer

4

TRY IT 7.2

Simplify: $18\left(-4\right)\div{\left(-2\right)}^{3}$ .

Show answer

9

EXAMPLE 8

Simplify: $-30\div 2+\left(-3\right)\left(-7\right)$ .

Solution

	$-30\div 2+\left(-3\right)\left(-7\right)$
Multiply and divide left to right, so divide first.	$-15+\left(-3\right)\left(-7\right)$
Multiply.	$-15+21$
Add.	$6$

TRY IT 8.1

Simplify: $-27\div 3+\left(-5\right)\left(-6\right)$ .

Show answer

21

TRY IT 8.2

Simplify: $-32\div 4+\left(-2\right)\left(-7\right)$ .

Show answer

6

Evaluate Variable Expressions with Integers

Remember that to evaluate an expression means to substitute a number for the variable in the expression. Now we can use negative numbers as well as positive numbers.

EXAMPLE 9

When $n=-5$ , evaluate: a) $n+1$ b) $\text{-}n+1$ .

Solution

a)



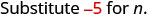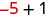Simplify.	−4

b)



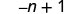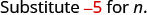Simplify.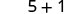
Add.	6

TRY IT 9.1

When $n=-8$ , evaluate a) $n+2$ b) $\text{-}n+2$ .

Show answer

a) $-6$ b) 10

TRY IT 9.2

When $y=-9$ , evaluate a) $y+8$ b) $\text{-}y+8$ .

Show answer

a) $-1$ b) 17

EXAMPLE 10

Evaluate ${\left(x+y\right)}^{2}$ when $x=-18$ and $y=24$ .

Solution


	${\left(-18+24\right)}^{2}$
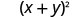Add inside parenthesis.	(6)²
Simplify.	36

TRY IT 10.1

Evaluate ${\left(x+y\right)}^{2}$ when $x=-15$ and $y=29$ .

Show answer

196

TRY IT 10.2

Evaluate ${\left(x+y\right)}^{3}$ when $x=-8$ and $y=10$ .

Show answer

8

EXAMPLE 11

Evaluate $20-z$ when a) $z=12$ and b) $z=-12$ .

Solution

a)



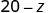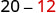Subtract.	8

b)



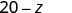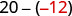Subtract.	32

TRY IT 11.1

Evaluate: $17-k$ when a) $k=19$ and b) $k=-19$ .

Show answer

a) $-2$ b) 36

TRY IT 11.2

Evaluate: $-5-b$ when a) $b=14$ and b) $b=-14$ .

Show answer

a) $-19$ b) 9

EXAMPLE 12

Evaluate: $2{x}^{2}+3x+8$ when $x=4$ .

Solution

Substitute $4\phantom{\rule{0.2em}{0ex}}\text{for}\phantom{\rule{0.2em}{0ex}}x$ . Use parentheses to show multiplication.


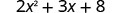Substitute.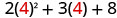
Evaluate exponents.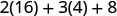
Multiply.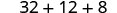
Add.	52

TRY IT 12.1

Evaluate: $3{x}^{2}-2x+6$ when $x=-3$ .

Show answer

39

TRY IT 12.2

Evaluate: $4{x}^{2}-x-5$ when $x=-2$ .

Show answer

13

Translate Phrases to Expressions with Integers

Our earlier work translating English to algebra also applies to phrases that include both positive and negative numbers.

EXAMPLE 13

Translate and simplify: the sum of 8 and $-12$ , increased by 3

Solution

	the sum of 8 and $-12$ , increased by 3.
Translate.	$\left[8+\left(-12\right)\right]+3$
Simplify. Be careful not to confuse the brackets with an absolute value sign.	$\left(-4\right)+3$
Add.	$-1$

TRY IT 13.1

Translate and simplify the sum of 9 and $-16$ , increased by 4

Show answer

$\left(9+\left(-16\right)\right)+4-3$

TRY IT 13.2

Translate and simplify the sum of $-8$ and $-12$ , increased by 7

Show answer

$\left(-8+\left(-12\right)\right)+7-13$

When we first introduced the operation symbols, we saw that the expression may be read in several ways. They are listed in the chart below.

$a-b$

$a$ minus $b$
the difference of $a$ and $b$
$b$ subtracted from $a$
$b$ less than $a$

Be careful to get a and b in the right order!

EXAMPLE 14

Translate and then simplify a) the difference of 13 and $-21$ b) subtract 24 from $-19$ .

Solution

a) Translate. Simplify.	$\begin{array}{c}\text{the}\phantom{\rule{0.2em}{0ex}}\mathbf{\text{difference}}\phantom{\rule{0.2em}{0ex}}\mathit{\text{of}}\phantom{\rule{0.2em}{0ex}}13\phantom{\rule{0.2em}{0ex}}\mathit{\text{and}}\phantom{\rule{0.2em}{0ex}}-21\\ 13-\left(-21\right)\\ 34\end{array}$
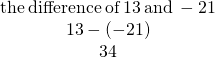b) Translate. Remember, “subtract $b$ from $a$ means $a-b$ . Simplify.	$\begin{array}{c}\mathbf{\text{subtract}}\phantom{\rule{0.2em}{0ex}}24\phantom{\rule{0.2em}{0ex}}\mathbf{\text{from}}\phantom{\rule{0.2em}{0ex}}-19\\ -19-24\\ -43\end{array}$

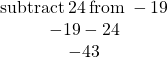TRY IT 14.1

Translate and simplify a) the difference of 14 and $-23$ b) subtract 21 from $-17$ .

Show answer

a) $14-\left(-23\right);37$ b) $-17-21;-38$

TRY IT 14.2

Translate and simplify a) the difference of 11 and $-19$ b) subtract 18 from $-11$ .

Show answer

a) $11-\left(-19\right);30$ b) $-11-18;-29$

Once again, our prior work translating English to algebra transfers to phrases that include both multiplying and dividing integers. Remember that the key word for multiplication is “product” and for division is “quotient.”

EXAMPLE 15

Translate to an algebraic expression and simplify if possible: the product of $-2$ and 14

Solution

	$\text{the product}\phantom{\rule{0.2em}{0ex}}\mathit{\text{of}}\phantom{\rule{0.2em}{0ex}}-2\phantom{\rule{0.2em}{0ex}}\mathit{\text{and}}\phantom{\rule{0.2em}{0ex}}14$
Translate.	$\left(-2\right)\left(14\right)$
Simplify.	$-28$

TRY IT 15.1

Translate to an algebraic expression and simplify if possible: the product of $-5$ and 12

Show answer

$-5\left(12\right);-60$

TRY IT 15.2

Translate to an algebraic expression and simplify if possible: the product of 8 and $-13$ .

Show answer

$-8\left(13\right);-104$

EXAMPLE 16

Translate to an algebraic expression and simplify if possible: the quotient of $-56$ and $-7$ .

Solution

	$\text{the quotient}\phantom{\rule{0.2em}{0ex}}\mathit{\text{of}}\phantom{\rule{0.2em}{0ex}}-56\phantom{\rule{0.2em}{0ex}}\mathit{\text{and}}\phantom{\rule{0.2em}{0ex}}-7$
Translate.	$-56\div \left(-7\right)$
Simplify.	$8$

TRY IT 16.1

Translate to an algebraic expression and simplify if possible: the quotient of $-63$ and $-9$ .

Show answer

$-63\div \left(-9\right);7$

TRY IT 16.2

Translate to an algebraic expression and simplify if possible: the quotient of $-72$ and $-9$ .

Show answer

$-72\div \left(-9\right);8$

Use Integers in Applications

We’ll outline a plan to solve applications. It’s hard to find something if we don’t know what we’re looking for or what to call it! So when we solve an application, we first need to determine what the problem is asking us to find. Then we’ll write a phrase that gives the information to find it. We’ll translate the phrase into an expression and then simplify the expression to get the answer. Finally, we summarize the answer in a sentence to make sure it makes sense.

EXAMPLE 17

The temperature in Sparwood, British Columbia, one morning was 11 degrees. By mid-afternoon, the temperature had dropped to $-9$ degrees. What was the difference of the morning and afternoon temperatures?

Solution

This is a table with two columns. The left column includes steps to solve the problem. The right column includes the math to solve the problem. In the first row, the left column says “Step 1. Read the problem. Make sure all the words and ideas are understood.” The right column is blank. In the second row, the left column says “Step 2. Identify what we are asked to find”. The right column says, “the difference of the morning and afternoon temperatures.” In the third row, the left column says, “Step 3. Write a phrase that gives the information to find it.” Next to this in the right column, it says “the difference of 11 and negative 9.” In the fourth row, the left column says, “Step 4. Translate the phrase to an expression.” The right column contains 11 minus negative 9. In the fifth row, the left column says, “Step 5. Simplify the expression.” The right column contains 20. The final row says, “Step five. Write a complete sentence that answers the question.” Next to this in the right column, it says “the difference in temperatures was 20 degrees.”

TRY IT 17.1

The temperature in Whitehorse, Yukon, one morning was 15 degrees. By mid-afternoon the temperature had dropped to 30 degrees below zero. What was the difference in the morning and afternoon temperatures?

Show answer

The difference in temperatures was 45 degrees.

TRY IT 17.2

The temperature in Quesnel, BC, was $-6$ degrees at lunchtime. By sunset the temperature had dropped to $-15$ degrees. What was the difference in the lunchtime and sunset temperatures?

Show answer

The difference in temperatures was 9 degrees.

HOW TO: Apply a Strategy to Solve Applications with Integers

Read the problem. Make sure all the words and ideas are understood
Identify what we are asked to find.
Write a phrase that gives the information to find it.
Translate the phrase to an expression.
Simplify the expression.
Answer the question with a complete sentence.

EXAMPLE 18

The Mustangs football team received three penalties in the third quarter. Each penalty gave them a loss of fifteen yards. What is the number of yards lost?

Solution

Step 1. Read the problem. Make sure all the words and ideas are understood.
Step 2. Identify what we are asked to find.	the number of yards lost
Step 3. Write a phrase that gives the information to find it.	three times a 15-yard penalty
Step 4. Translate the phrase to an expression.	$3\left(-15\right)$
Step 5. Simplify the expression.	$-45$
Step 6. Answer the question with a complete sentence.	The team lost 45 yards.

TRY IT 18.1

The Bears played poorly and had seven penalties in the game. Each penalty resulted in a loss of 15 yards. What is the number of yards lost due to penalties?

Show answer

The Bears lost 105 yards.

TRY IT 18.2

Bill uses the ATM on campus because it is convenient. However, each time he uses it he is charged a $2 fee. Last month he used the ATM eight times. How much was his total fee for using the ATM?

Show answer

A $16 fee was deducted from his checking account.

Key Concepts

Multiplication and Division of Two Signed Numbers
- Same signs—Product is positive
- Different signs—Product is negative
Strategy for Applications
1. Identify what you are asked to find.
2. Write a phrase that gives the information to find it.
3. Translate the phrase to an expression.
4. Simplify the expression.
5. Answer the question with a complete sentence.

Practice Makes Perfect

Multiply Integers

In the following exercises, multiply.

1. $-4\cdot8$	2. $-3\cdot9$
3. $9\left(-7\right)$	4. $13\left(-5\right)$
5. $-1\cdot6$	6. $-1\cdot3$
7. $-1\left(-14\right)$	8. $-1\left(-19\right)$

Divide Integers

In the following exercises, divide.

9. $-24\div6$	10. $35\div\left(-7\right)$
11. $-52\div\left(-4\right)$	12. $-84\div\left(-6\right)$
13. $-180\div15$	14. $-192\div12$

Simplify Expressions with Integers

In the following exercises, simplify each expression.

15. $5\left(-6\right)+7\left(-2\right)-3$	16. $8\left(-4\right)+5\left(-4\right)-6$
17. ${\left(-2\right)}^{6}$	18. ${\left(-3\right)}^{5}$
19. $\text{-}{4}^{2}$	20. $\text{-}{6}^{2}$
21. $-3\left(-5\right)\left(6\right)$	22. $-4\left(-6\right)\left(3\right)$
23. $\left(8-11\right)\left(9-12\right)$	24. $\left(6-11\right)\left(8-13\right)$
25. $26-3\left(2-7\right)$	26. $23-2\left(4-6\right)$
27. $65\div\left(-5\right)+\left(-28\right)\div\left(-7\right)$	28. $52\div\left(-4\right)+\left(-32\right)\div\left(-8\right)$
29. $9-2\left[3-8\left(-2\right)\right]$	30. $11-3\left[7-4\left(-2\right)\right]$
31. ${\left(-3\right)}^{2}-24\div\left(8-2\right)$	32. ${\left(-4\right)}^{2}-32\div\left(12-4\right)$

Evaluate Variable Expressions with Integers

In the following exercises, evaluate each expression.

33. $y+\left(-14\right)$ when a) $y=-33$ b) $y=30$	34. $x+\left(-21\right)$ when a) $x=-27$ b) $x=44$
35. a) $a+3$ when $a=-7$ b) $\text{-}a+3$ when $a=-7$	36. a) $d+\left(-9\right)$ when $d=-8$ b) $\text{-}d+\left(-9\right)$ when $d=-8$
37. $m+n$ when $m=-15,n=7$	38. $p+q$ when $p=-9,q=17$
39. $r+s$ when $r=-9,s=-7$	40. $t+u$ when $t=-6,u=-5$
41. ${\left(x+y\right)}^{2}$ when $x=-3,y=14$	42. ${\left(y+z\right)}^{2}$ when $y=-3,z=15$
43. $-2x+17$ when a) $x=8$ b) $x=-8$	44. $-5y+14$ when a) $y=9$ b) $y=-9$
45. $10-3m$ when a) $m=5$ b) $m=-5$	46. $18-4n$ when a) $n=3$ b) $n=-3$
47. $2{w}^{2}-3w+7$ when $w=-2$	48. $3{u}^{2}-4u+5$ when $u=-3$
49. $9a-2b-8$ when $a=-6\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}b=-3$	50. $7m-4n-2$ when $m=-4\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}n=-9$

Translate English Phrases to Algebraic Expressions

In the following exercises, translate to an algebraic expression and simplify if possible.

51. the sum of 3 and $-15$ , increased by 7	52. the sum of $-8$ and $-9$ , increased by 23
53. the difference of 10 and $-18$	54. subtract 11 from $-25$
55. the difference of $-5$ and $-30$	56. subtract $-6$ from $-13$
57. the product of $-3$ and $15$	58. the product of $-4$ and $16$
59. the quotient of $-60$ and $-20$	60. the quotient of $-40$ and $-20$
61. the quotient of $-6$ and the sum of a and b	62. the quotient of $-7$ and the sum of m and n
63. the product of $-10$ and the difference of $p\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}q$	64. the product of $-13$ and the difference of $c\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}d$

Use Integers in Applications

In the following exercises, solve.

65. Temperature On January $15$ , the high temperature in Lytton, British Columbia, was $84$ ° . That same day, the high temperature in Fort Nelson, British Columbia was $-12$ °. What was the difference between the temperature in Lytton and the temperature in Embarrass?	66. Temperature On January $21$ , the high temperature in Palm Springs, California, was $89$ °, and the high temperature in Whitefield, New Hampshire was $-31$ °. What was the difference between the temperature in Palm Springs and the temperature in Whitefield?
67. Football At the first down, the Chargers had the ball on their 25 yard line. On the next three downs, they lost 6 yards, gained 10 yards, and lost 8 yards. What was the yard line at the end of the fourth down?	68. Football At the first down, the Steelers had the ball on their 30 yard line. On the next three downs, they gained 9 yards, lost 14 yards, and lost 2 yards. What was the yard line at the end of the fourth down?
69. Checking Account Ester has $124 in her checking account. She writes a check for $152. What is the new balance in her checking account?	70. Checking Account Selina has $165 in her checking account. She writes a check for $207. What is the new balance in her checking account?
71. Checking Account Kevin has a balance of $-\$38$ in his checking account. He deposits $225 to the account. What is the new balance?	72. Checking Account Reymonte has a balance of $-\$49$ in his checking account. He deposits $281 to the account. What is the new balance?

Everyday Math

73. Stock market Javier owns 300 shares of stock in one company. On Tuesday, the stock price dropped $12 per share. What was the total effect on Javier’s portfolio?

74. Weight loss In the first week of a diet program, eight women lost an average of 3 pounds each. What was the total weight change for the eight women?

Writing Exercises

75. In your own words, state the rules for multiplying integers.	76. In your own words, state the rules for dividing integers.
77. Why is $-{2}^{4}\ne {\left(-2\right)}^{4}?$	78. Why is $-{4}^{3}={\left(-4\right)}^{3}?$

Answers

1. $-32$	3. $-63$	5. $-6$
7. 14	9. $-4$	11. 13
13. $-12$	15. $-47$	17. 64
19. $-16$	21. 90	23. 9
25. 41	27. $-9$	29. $-29$
31. 5	33. a) $-47$ b) 16	35. a) $-4$ b) 10
37. $-8$	39. $-16$	41. 121
43. a) 1 b) 33	45. a) $-5$ b) 25	47. 21
49. $-56$	51. $\left(3+\left(-15\right)\right)+7;-5$	53. $10-\left(-18\right);28$
55. $-5-\left(-30\right);25$	57. $-3\cdot 15;-45$	59. $-60\div\left(-20\right);3$
61. $\frac{-6}{a+b}$	63. $-10\left(p-q\right)$	65. $96$ °
67. 21	69. $\text{-}\$28$	71. $187
73. $\text{-}\$3600$	75. Answers may vary	77. Answers may vary

Attributions

This chapter has been adapted from “Multiply and Divide Integers” in Elementary Algebra (OpenStax) by Lynn Marecek and MaryAnne Anthony-Smith, which is under a CC BY 4.0 Licence. Adapted by Izabela Mazur. See the Copyright page for more information.

License

Icon for the Creative Commons Attribution 4.0 International License

Multiply Integers

Divide Integers

Simplify Expressions with Integers

Evaluate Variable Expressions with Integers

Translate Phrases to Expressions with Integers

Use Integers in Applications

Key Concepts

Practice Makes Perfect

Multiply Integers

Divide Integers

Simplify Expressions with Integers

Evaluate Variable Expressions with Integers

Translate English Phrases to Algebraic Expressions

Use Integers in Applications

Everyday Math

Writing Exercises

Answers

Attributions

License

Share This Book