CHAPTER 3 Measurement, Perimeter, Area, and Volume
3.4 Solve Geometry Applications: Circles and Irregular Figures
Learning Objectives
By the end of this section, you will be able to:
- Use the properties of circles
- Find the area of irregular figures
In this section, we’ll continue working with geometry applications. We will add several new formulas to our collection of formulas. To help you as you do the examples and exercises in this section, we will show the Problem Solving Strategy for Geometry Applications here.
Problem Solving Strategy for Geometry Applications
- Read the problem and make sure you understand all the words and ideas. Draw the figure and label it with the given information.
- Identify what you are looking for.
- Name what you are looking for. Choose a variable to represent that quantity.
- Translate into an equation by writing the appropriate formula or model for the situation. Substitute in the given information.
- Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
Use the Properties of Circles
We’ll refer to the properties of circles as we use them to solve applications.
Properties of Circles
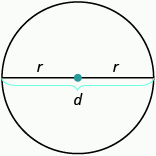
 is the length of the radius
is the length of the radius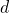 is the length of the diametre
is the length of the diametre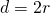
- Circumference is the perimeter of a circle. The formula for circumference is
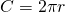
- The formula for area of a circle is
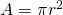
Remember, that we approximate ![]() with
with ![]() or
or ![]() depending on whether the radius of the circle is given as a decimal or a fraction. If you use the
depending on whether the radius of the circle is given as a decimal or a fraction. If you use the ![]() key on your calculator to do the calculations in this section, your answers will be slightly different from the answers shown. That is because the
key on your calculator to do the calculations in this section, your answers will be slightly different from the answers shown. That is because the ![]() key uses more than two decimal places.
key uses more than two decimal places.
EXAMPLE 1
A circular sandbox has a radius of ![]() feet. Find the a) circumference and b) area of the sandbox.
feet. Find the a) circumference and b) area of the sandbox.
| Step 1. Read the problem. Draw the figure and label it with the given information. | 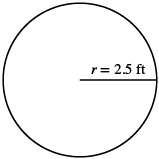 |
| Step 2. Identify what you are looking for. | the circumference of the circle |
| Step 3. Name. Choose a variable to represent it. | Let c = circumference of the circle |
| Step 4. Translate. Write the appropriate formula Substitute |
|
| Step 5. Solve the equation. | |
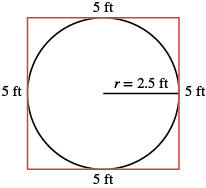
| Step 6. Check. Does this answer make sense? Yes. If we draw a square around the circle, its sides would be 5 ft (twice the radius), so its perimeter would be 20 ft. This is slightly more than the circle’s circumference, 15.7 ft. |
 |
| Step 7. Answer the question. | The circumference of the sandbox is 15.7 feet. |
b)
| Step 1. Read the problem. Draw the figure and label it with the given information |  |
| Step 2. Identify what you are looking for. | the area of the circle |
| Step 3. Name. Choose a variable to represent it. | Let A = the area of the circle |
| Step 4. Translate. Write the appropriate formula Substitute |
|
| Step 5. Solve the equation. | |
| Step 6. Check. Yes. If we draw a square around the circle, its sides would be 5 ft, as shown in part a). So the area of the square would be 25 sq. ft. This is slightly more than the circle’s area, 19.625 sq. ft. |
|
| Step 7. Answer the question. | The area of the circle is 19.625 square feet. |
TRY IT 1.1
A circular mirror has radius of ![]() inches. Find the a) circumference and b) area of the mirror.
inches. Find the a) circumference and b) area of the mirror.
Show answer
- 31.4 in.
- 78.5 sq. in.
TRY IT 1.2
A circular spa has radius of ![]() feet. Find the a) circumference and b) area of the spa.
feet. Find the a) circumference and b) area of the spa.
Show answer
- 28.26 ft
- 63.585 sq. ft
We usually see the formula for circumference in terms of the radius ![]() of the circle:
of the circle:
But since the diametre of a circle is two times the radius, we could write the formula for the circumference in terms ![]() .
.
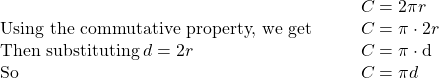
We will use this form of the circumference when we’re given the length of the diametre instead of the radius.
EXAMPLE 2
A circular table has a diametre of four feet. What is the circumference of the table?
| Step 1. Read the problem. Draw the figure and label it with the given information. | 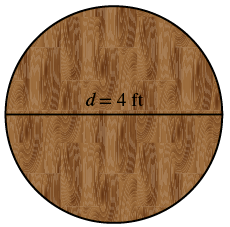 |
| Step 2. Identify what you are looking for. | the circumference of the table |
| Step 3. Name. Choose a variable to represent it. | Let c = the circumference of the table |
| Step 4. Translate. Write the appropriate formula for the situation. Substitute. |
|
| Step 5. Solve the equation, using 3.14 for |
|
| Step 6. Check: If we put a square around the circle, its side would be 4. The perimeter would be 16. It makes sense that the circumference of the circle, 12.56, is a little less than 16. |
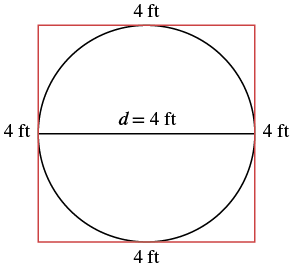 |
| Step 7. Answer the question. | The diametre of the table is 12.56 square feet |
TRY IT 2.1
Find the circumference of a circular fire pit whose diametre is ![]() feet.
feet.
Show answer
17.27 ft
TRY IT 2.2
If the diametre of a circular trampoline is ![]() feet, what is its circumference?
feet, what is its circumference?
Show answer
37.68 ft
EXAMPLE 3
Find the diametre of a circle with a circumference of ![]() centimetres.
centimetres.
| Step 1. Read the problem. Draw the figure and label it with the given information. | 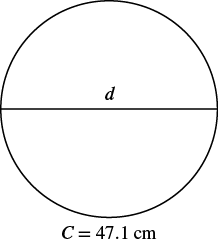 |
| Step 2. Identify what you are looking for. | the diametre of the circle |
| Step 3. Name. Choose a variable to represent it. | Let d = the diametre of the circle |
| Step 4. Translate. | |
| Write the formula. Substitute, using 3.14 to approximate |
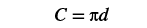 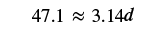 |
| Step 5. Solve. | 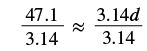 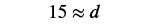 |
| Step 6. Check: |
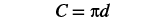 |
| Step 7. Answer the question. | The diametre of the circle is approximately 15 centimetres. |
TRY IT 3.1
Find the diametre of a circle with circumference of ![]() centimetres.
centimetres.
Show answer
30 cm
TRY IT 3.2
Find the diametre of a circle with circumference of ![]() feet.
feet.
Show answer
110 ft
Find the Area of Irregular Figures
So far, we have found area for rectangles, triangles, trapezoids, and circles. An irregular figure is a figure that is not a standard geometric shape. Its area cannot be calculated using any of the standard area formulas. But some irregular figures are made up of two or more standard geometric shapes. To find the area of one of these irregular figures, we can split it into figures whose formulas we know and then add the areas of the figures.
EXAMPLE 4
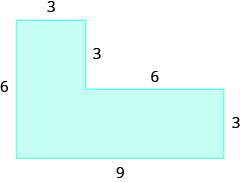
Find the area of the shaded region.
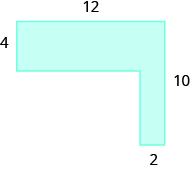
The given figure is irregular, but we can break it into two rectangles. The area of the shaded region will be the sum of the areas of both rectangles.
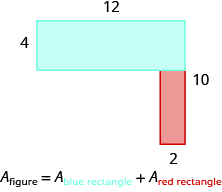
The blue rectangle has a width of ![]() and a length of
and a length of ![]() . The red rectangle has a width of
. The red rectangle has a width of ![]() , but its length is not labeled. The right side of the figure is the length of the red rectangle plus the length of the blue rectangle. Since the right side of the blue rectangle is
, but its length is not labeled. The right side of the figure is the length of the red rectangle plus the length of the blue rectangle. Since the right side of the blue rectangle is ![]() units long, the length of the red rectangle must be
units long, the length of the red rectangle must be ![]() units.
units.
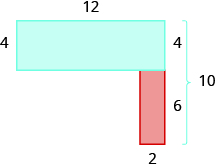
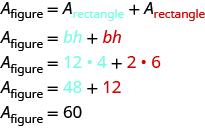
The area of the figure is ![]() square units.
square units.
Is there another way to split this figure into two rectangles? Try it, and make sure you get the same area.
TRY IT 4.1
Find the area of each shaded region:
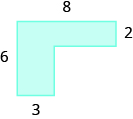
Show answer
28 sq. units
TRY IT 4.2
Find the area of each shaded region:
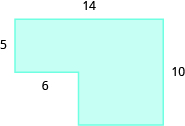
Show answer
110 sq. units
EXAMPLE 5
Find the area of the shaded region.
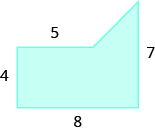
We can break this irregular figure into a triangle and rectangle. The area of the figure will be the sum of the areas of triangle and rectangle.
The rectangle has a length of ![]() units and a width of
units and a width of ![]() units.
units.
We need to find the base and height of the triangle.
Since both sides of the rectangle are ![]() , the vertical side of the triangle is
, the vertical side of the triangle is ![]() , which is
, which is ![]() .
.
The length of the rectangle is ![]() , so the base of the triangle will be
, so the base of the triangle will be ![]() , which is
, which is ![]() .
.
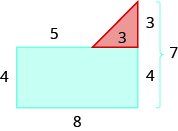
Now we can add the areas to find the area of the irregular figure.

The area of the figure is ![]() square units.
square units.
TRY IT 5.1
Find the area of each shaded region.

Show answer
36.5 sq. units
TRY IT 5.2
Find the area of each shaded region.
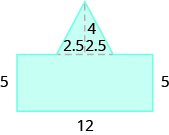
Show answer
70 sq. units
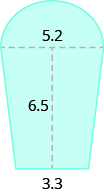
EXAMPLE 6
A high school track is shaped like a rectangle with a semi-circle (half a circle) on each end. The rectangle has length ![]() metres and width
metres and width ![]() metres. Find the area enclosed by the track. Round your answer to the nearest hundredth.
metres. Find the area enclosed by the track. Round your answer to the nearest hundredth.

We will break the figure into a rectangle and two semi-circles. The area of the figure will be the sum of the areas of the rectangle and the semicircles.

The rectangle has a length of ![]() m and a width of
m and a width of ![]() m. The semi-circles have a diametre of
m. The semi-circles have a diametre of ![]() m, so each has a radius of
m, so each has a radius of ![]() m.
m.
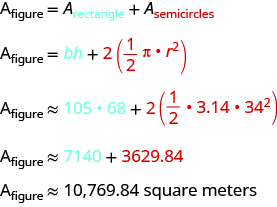
TRY IT 6.1
Find the area:
Show answer
103.2 sq. units
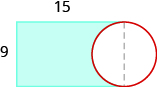
TRY IT 6.2
Find the area:
Show answer
38.24 sq. units
Key Concepts
- Problem Solving Strategy for Geometry Applications
- Read the problem and make sure you understand all the words and ideas. Draw the figure and label it with the given information.
- Identify what you are looking for.
- Name what you are looking for. Choose a variable to represent that quantity.
- Translate into an equation by writing the appropriate formula or model for the situation. Substitute in the given information.
- Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
- Properties of Circles
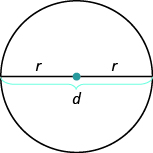
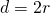
- Circumference:
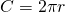 or
or 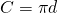
- Area:
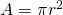
Glossary
- irregular figure
- An irregular figure is a figure that is not a standard geometric shape. Its area cannot be calculated using any of the standard area formulas.
Practice Makes Perfect
Use the Properties of Circles
In the following exercises, solve using the properties of circles.
| 1. The lid of a paint bucket is a circle with radius |
2. An extra-large pizza is a circle with radius |
| 3. A farm sprinkler spreads water in a circle with radius of |
4. A circular rug has radius of |
| 5. A reflecting pool is in the shape of a circle with diametre of |
6. A turntable is a circle with diametre of |
| 7. A circular saw has a diametre of |
8. A round coin has a diametre of |
| 9. A barbecue grill is a circle with a diametre of |
10. The top of a pie tin is a circle with a diametre of |
| 11. A circle has a circumference of |
12. A circle has a circumference of |
| 13. A circle has a circumference of |
14. A circle has a circumference of |
In the following exercises, find the radius of the circle with given circumference.
| 15. A circle has a circumference of |
16. A circle has a circumference of |
| 17. A circle has a circumference of |
18. A circle has a circumference of |
Find the Area of Irregular Figures
In the following exercises, find the area of the irregular figure. Round your answers to the nearest hundredth.
19. 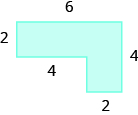 |
20. 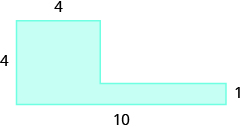 |
21. 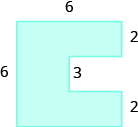 |
22. 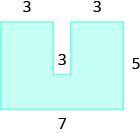 |
23. 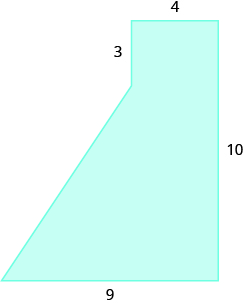 |
24. 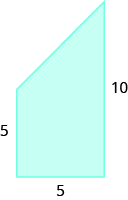 |
25. 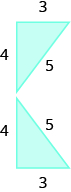 |
26. 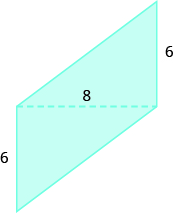 |
27. 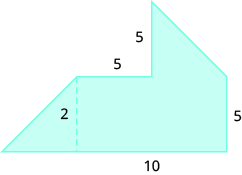 |
28. 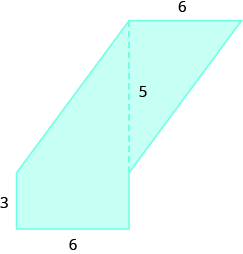 |
29. 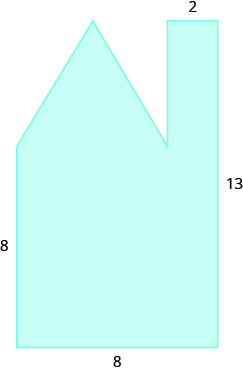 |
30. 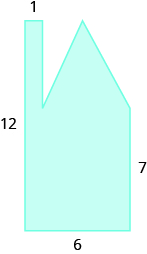 |
31.  |
32. 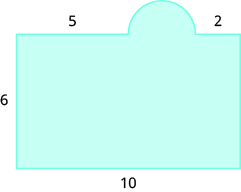 |
33. 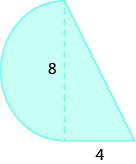 |
34. 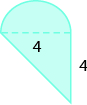 |
35. 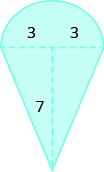 |
36. 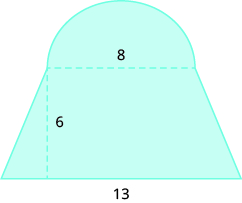 |
37. 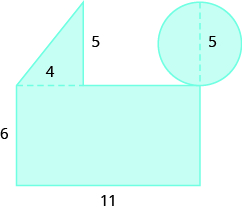 |
38. 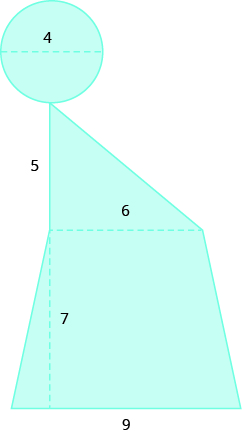 |
In the following exercises, solve.
|
39. A city park covers one block plus parts of four more blocks, as shown. The block is a square with sides
|
40. A gift box will be made from a rectangular piece of cardboard measuring
|
|
41. Perry needs to put in a new lawn. His lot is a rectangle with a length of
|
42. Denise is planning to put a deck in her back yard. The deck will be a
|
Everyday Math
|
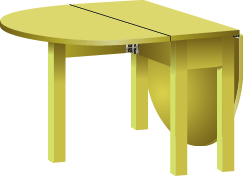
43. Area of a Tabletop Yuki bought a drop-leaf kitchen table. The rectangular part of the table is a
|
44. Painting Leora wants to paint the nursery in her house. The nursery is an |
Writing Exercises
| 45. Describe two different ways to find the area of this figure, and then show your work to make sure both ways give the same area.
|
46. A circle has a diametre of |
Answers
| 1.
a) 43.96 in. b) 153.86 sq. in. |
3.
a) 53.38 ft b) 226.865 sq. ft |
5. 62.8 ft |
| 7. 37.68 in. | 9. 6.908 ft | 11. 52 in. |
| 13. 5.5 m | 15. 24 ft | 17. 6.5 mi |
| 19. 16 sq. units | 21. 30 sq. units | 23. 57.5 sq. units |
| 25. 12 sq. units | 27. 67.5 sq. units | 29. 89 sq. units |
| 31. 44.81 sq. units | 33. 41.12 sq. units | 35. 35.13 sq. units |
| 37. 95.625 sq. units | 39. 187,500 sq. ft | 41. 9400 sq. ft |
| 43. a) 6.5325 sq. ft b) 10.065 sq. ft | 45. Answers will vary. |
Attributions
This chapter has been adapted from “Solve Geometry Applications: Circles and Irregular Figures” in Prealgebra (OpenStax) by Lynn Marecek, MaryAnne Anthony-Smith, and Andrea Honeycutt Mathis, which is under a CC BY 4.0 Licence. Adapted by Izabela Mazur. See the Copyright page for more information.