CHAPTER 3 Measurement, Perimeter, Area, and Volume
3.2 Use Properties of Rectangles, Triangles, and Trapezoids
Learning Objectives
By the end of this section, you will be able to:
- Understand linear, square, and cubic measure
- Use properties of rectangles
- Use properties of triangles
- Use properties of trapezoids
Understand Linear, Square, and Cubic Measure
When you measure your height or the length of a garden hose, you use a ruler or tape measure (Figure.1). A tape measure might remind you of a line—you use it for linear measure, which measures length. Inch, foot, yard, mile, centimetre and metre are units of linear measure.

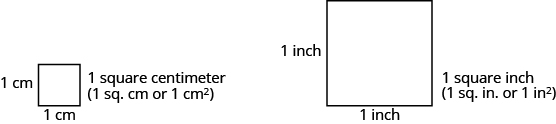
When you want to know how much tile is needed to cover a floor, or the size of a wall to be painted, you need to know the area, a measure of the region needed to cover a surface. Area is measured is square units. We often use square inches, square feet, square centimetres, or square miles to measure area. A square centimetre is a square that is one centimetre (cm) on each side. A square inch is a square that is one inch on each side (Figure.2).
Square measures have sides that are each ![]() unit in length.
unit in length.
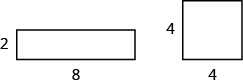
(Figure.3) shows a rectangular rug that is ![]() feet long by
feet long by ![]() feet wide. Each square is
feet wide. Each square is ![]() foot wide by
foot wide by ![]() foot long, or
foot long, or ![]() square foot. The rug is made of
square foot. The rug is made of ![]() squares. The area of the rug is
squares. The area of the rug is![]() square feet.
square feet.

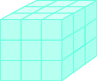
When you measure how much it takes to fill a container, such as the amount of gasoline that can fit in a tank, or the amount of medicine in a syringe, you are measuring volume. Volume is measured in cubic units such as cubic inches or cubic centimetres. When measuring the volume of a rectangular solid, you measure how many cubes fill the container. We often use cubic centimetres, cubic inches, and cubic feet. A cubic centimetre is a cube that measures one centimetre on each side, while a cubic inch is a cube that measures one inch on each side (Figure.4).
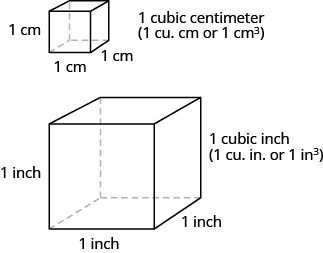
Suppose the cube in (Figure.5) measures ![]() inches on each side and is cut on the lines shown. How many little cubes does it contain? If we were to take the big cube apart, we would find
inches on each side and is cut on the lines shown. How many little cubes does it contain? If we were to take the big cube apart, we would find ![]() little cubes, with each one measuring one inch on all sides. So each little cube has a volume of
little cubes, with each one measuring one inch on all sides. So each little cube has a volume of ![]() cubic inch, and the volume of the big cube is
cubic inch, and the volume of the big cube is ![]() cubic inches.
cubic inches.
A cube that measures 3 inches on each side is made up of 27 one-inch cubes, or 27 cubic inches.
EXAMPLE 1
For each item, state whether you would use linear, square, or cubic measure:
a) amount of carpeting needed in a room
b) extension cord length
c) amount of sand in a sandbox
d) length of a curtain rod
e) amount of flour in a canister
f) size of the roof of a doghouse.
| a) You are measuring how much surface the carpet covers, which is the area. | square measure |
| b) You are measuring how long the extension cord is, which is the length. | linear measure |
| c) You are measuring the volume of the sand. | cubic measure |
| d) You are measuring the length of the curtain rod. | linear measure |
| e) You are measuring the volume of the flour. | cubic measure |
| f) You are measuring the area of the roof. | square measure |
TRY IT 1.1
Determine whether you would use linear, square, or cubic measure for each item.
a) amount of paint in a can b) height of a tree c) floor of your bedroom d) diametre of bike wheel e) size of a piece of sod f) amount of water in a swimming pool
Show answer
- cubic
- linear
- square
- linear
- square
- cubic
TRY IT 1.2
Determine whether you would use linear, square, or cubic measure for each item.
a) volume of a packing box b) size of patio c) amount of medicine in a syringe d) length of a piece of yarn e) size of housing lot f) height of a flagpole
Show answer
- cubic
- square
- cubic
- linear
- square
- linear
Many geometry applications will involve finding the perimeter or the area of a figure. There are also many applications of perimeter and area in everyday life, so it is important to make sure you understand what they each mean.
Picture a room that needs new floor tiles. The tiles come in squares that are a foot on each side—one square foot. How many of those squares are needed to cover the floor? This is the area of the floor.
Next, think about putting new baseboard around the room, once the tiles have been laid. To figure out how many strips are needed, you must know the distance around the room. You would use a tape measure to measure the number of feet around the room. This distance is the perimeter.
Perimeter and Area
The perimeter is a measure of the distance around a figure.
The area is a measure of the surface covered by a figure.
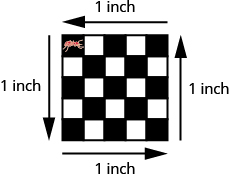
(Figure. 6) shows a square tile that is ![]() inch on each side. If an ant walked around the edge of the tile, it would walk
inch on each side. If an ant walked around the edge of the tile, it would walk ![]() inches. This distance is the perimeter of the tile.
inches. This distance is the perimeter of the tile.
Since the tile is a square that is ![]() inch on each side, its area is one square inch. The area of a shape is measured by determining how many square units cover the shape.
inch on each side, its area is one square inch. The area of a shape is measured by determining how many square units cover the shape.
![]()
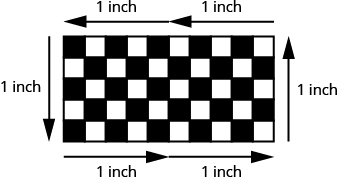
EXAMPLE 2
Each of two square tiles is ![]() square inch. Two tiles are shown together.
square inch. Two tiles are shown together.
a) What is the perimeter of the figure?
b) What is the area?

a) The perimeter is the distance around the figure. The perimeter is ![]() inches.
inches.
b) The area is the surface covered by the figure. There are ![]() square inch tiles so the area is
square inch tiles so the area is ![]() square inches.
square inches.
TRY IT 2.1
Find the a) perimeter and b) area of the figure:

Show answer
- 8 inches
- 3 sq. inches
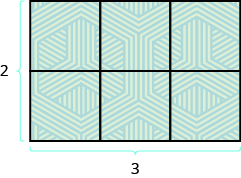
TRY IT 2.2
Find the a) perimeter and b) area of the figure:

Show answer
- 8 centimetres
- 4 sq. centimetres
Use the Properties of Rectangles
A rectangle has four sides and four right angles. The opposite sides of a rectangle are the same length. We refer to one side of the rectangle as the length, ![]() , and the adjacent side as the width,
, and the adjacent side as the width, ![]() . See (Figure.7).
. See (Figure.7).
A rectangle has four sides, and four right angles. The sides are labeled L for length and W for width.
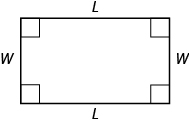
The perimeter, ![]() , of the rectangle is the distance around the rectangle. If you started at one corner and walked around the rectangle, you would walk
, of the rectangle is the distance around the rectangle. If you started at one corner and walked around the rectangle, you would walk ![]() units, or two lengths and two widths. The perimeter then is
units, or two lengths and two widths. The perimeter then is
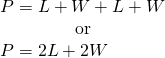
What about the area of a rectangle? Remember the rectangular rug from the beginning of this section. It was ![]() feet long by
feet long by ![]() feet wide, and its area was
feet wide, and its area was ![]() square feet. See (Figure.8). Since
square feet. See (Figure.8). Since ![]() , we see that the area,
, we see that the area, ![]() , is the length,
, is the length, ![]() , times the width,
, times the width, ![]() , so the area of a rectangle is
, so the area of a rectangle is ![]() .
.
The area of this rectangular rug is ![]() square feet, its length times its width.
square feet, its length times its width.
Properties of Rectangles
- Rectangles have four sides and four right
 ° angles.
° angles. - The lengths of opposite sides are equal.
- The perimeter,
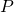 , of a rectangle is the sum of twice the length and twice the width. See (Figure 8).
, of a rectangle is the sum of twice the length and twice the width. See (Figure 8).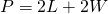
- The area,
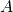 , of a rectangle is the length times the width.
, of a rectangle is the length times the width.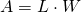
For easy reference as we work the examples in this section, we will state the Problem Solving Strategy for Geometry Applications here.
HOW TO: Use a Problem Solving Strategy for Geometry Applications
- Read the problem and make sure you understand all the words and ideas. Draw the figure and label it with the given information.
- Identify what you are looking for.
- Name what you are looking for. Choose a variable to represent that quantity.
- Translate into an equation by writing the appropriate formula or model for the situation. Substitute in the given information.
- Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
EXAMPLE 3
The length of a rectangle is ![]() metres and the width is
metres and the width is ![]() metres. Find a) the perimeter, and b) the area.
metres. Find a) the perimeter, and b) the area.
| a) | |
| Step 1. Read the problem. Draw the figure and label it with the given information. | 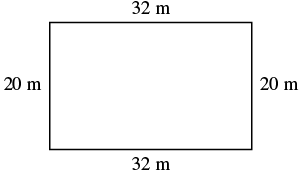 |
| Step 2. Identify what you are looking for. | the perimeter of a rectangle |
| Step 3. Name. Choose a variable to represent it. | Let P = the perimeter |
| Step 4. Translate. Write the appropriate formula. Substitute. |
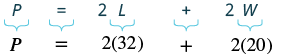 |
| Step 5. Solve the equation. | 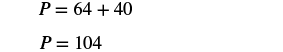 |
| Step 6. Check: | 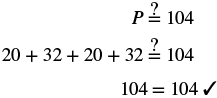 |
| Step 7. Answer the question. | The perimeter of the rectangle is 104 metres. |
| b) | |
| Step 1. Read the problem. Draw the figure and label it with the given information. | 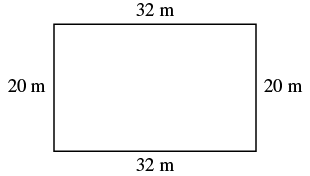 |
| Step 2. Identify what you are looking for. | the area of a rectangle |
| Step 3. Name. Choose a variable to represent it. | Let A = the area |
| Step 4. Translate. Write the appropriate formula. Substitute. |
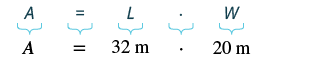 |
| Step 5. Solve the equation. |  |
| Step 6. Check: |  |
| Step 7. Answer the question. | The area of the rectangle is 60 square metres. |
TRY IT 3.1
The length of a rectangle is ![]() yards and the width is
yards and the width is ![]() yards. Find a) the perimeter and b) the area.
yards. Find a) the perimeter and b) the area.
Show answer
- 340 yd
- 6000 sq. yd
TRY IT 3.2
The length of a rectangle is ![]() feet and the width is
feet and the width is ![]() feet. Find a) the perimeter and b) the area.
feet. Find a) the perimeter and b) the area.
Show answer
- 220 ft
- 2976 sq. ft
EXAMPLE 4
Find the length of a rectangle with perimeter ![]() inches and width
inches and width ![]() inches.
inches.
| Step 1. Read the problem. Draw the figure and label it with the given information. | 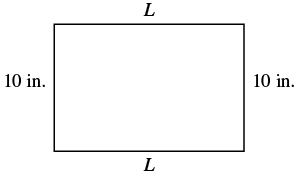 |
| Step 2. Identify what you are looking for. | the length of the rectangle |
| Step 3. Name. Choose a variable to represent it. | Let L = the length |
| Step 4. Translate. Write the appropriate formula. Substitute. |
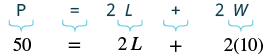 |
| Step 5. Solve the equation. | 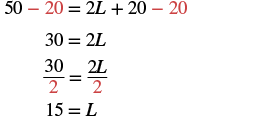 |
| Step 6. Check: | 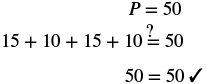 |
| Step 7. Answer the question. | The length is 15 inches. |
TRY IT 4.1
Find the length of a rectangle with a perimeter of ![]() inches and width of
inches and width of ![]() inches.
inches.
Show answer
15 in.
TRY IT 4.2
Find the length of a rectangle with a perimeter of ![]() yards and width of
yards and width of ![]() yards.
yards.
Show answer
9 yd
In the next example, the width is defined in terms of the length. We’ll wait to draw the figure until we write an expression for the width so that we can label one side with that expression.
EXAMPLE 5
The width of a rectangle is two inches less than the length. The perimeter is ![]() inches. Find the length and width.
inches. Find the length and width.
| Step 1. Read the problem. | |
| Step 2. Identify what you are looking for. | the length and width of the rectangle |
| Step 3. Name. Choose a variable to represent it.
Now we can draw a figure using these expressions for the length and width. |
Since the width is defined in terms of the length, we let L = length. The width is two feet less that the length, so we let L − 2 = width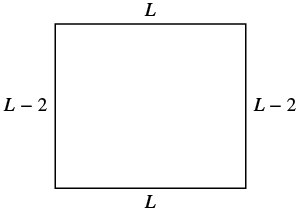 |
| Step 4.Translate. Write the appropriate formula. The formula for the perimeter of a rectangle relates all the information. Substitute in the given information. |
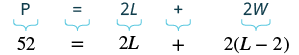 |
| Step 5. Solve the equation. | |
| Combine like terms. | |
| Add 4 to each side. | |
| Divide by 4. | |
| The length is 14 inches. | |
| Now we need to find the width. | |
| The width is L − 2. | 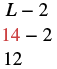 The width is 12 inches. |
| Step 6. Check: Since |
|
| Step 7. Answer the question. | The length is 14 feet and the width is 12 feet. |
TRY IT 5.1
The width of a rectangle is seven metres less than the length. The perimeter is ![]() metres. Find the length and width.
metres. Find the length and width.
Show answer
18 m, 11 m
TRY IT 5.2
The length of a rectangle is eight feet more than the width. The perimeter is ![]() feet. Find the length and width.
feet. Find the length and width.
Show answer
11 ft , 19 ft
EXAMPLE 6
The length of a rectangle is four centimetres more than twice the width. The perimeter is ![]() centimetres. Find the length and width.
centimetres. Find the length and width.
| Step 1. Read the problem. | |
| Step 2. Identify what you are looking for. | the length and width |
| Step 3. Name. Choose a variable to represent it. | let W = width The length is four more than twice the width. 2w + 4 = length 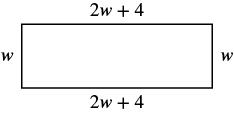 |
| Step 4.Translate. Write the appropriate formula and substitute in the given information. |
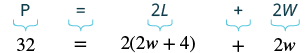 |
| Step 5. Solve the equation. | 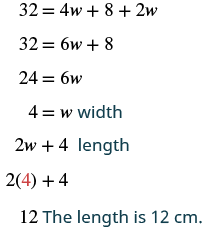 |
| Step 6. Check: | 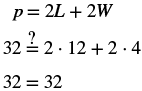 |
| Step 7. Answer the question. | The length is 12 cm and the width is 4 cm. |
TRY IT 6.1
The length of a rectangle is eight more than twice the width. The perimeter is ![]() feet. Find the length and width.
feet. Find the length and width.
Show answer
8 ft, 24 ft
TRY IT 6.2
The width of a rectangle is six less than twice the length. The perimeter is ![]() centimetres. Find the length and width.
centimetres. Find the length and width.
Show answer
5 cm, 4 cm
EXAMPLE 7
The area of a rectangular room is ![]() square feet. The length is
square feet. The length is ![]() feet. What is the width?
feet. What is the width?
| Step 1. Read the problem. | 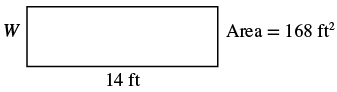 |
| Step 2. Identify what you are looking for. | the width of a rectangular room |
| Step 3. Name. Choose a variable to represent it. | Let W = width |
| Step 4.Translate. Write the appropriate formula and substitute in the given information. |
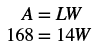 |
| Step 5. Solve the equation. | 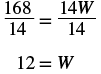 |
| Step 6. Check: | 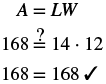 |
| Step 7. Answer the question. | The width of the room is 12 feet. |
TRY IT 7.1
The area of a rectangle is ![]() square feet. The length is
square feet. The length is ![]() feet. What is the width?
feet. What is the width?
Show answer
26 ft
TRY IT 7.2
The width of a rectangle is ![]() metres. The area is
metres. The area is ![]() square metres. What is the length?
square metres. What is the length?
Show answer
29 m
EXAMPLE 8
The perimeter of a rectangular swimming pool is ![]() feet. The length is
feet. The length is ![]() feet more than the width. Find the length and width.
feet more than the width. Find the length and width.
| Step 1. Read the problem. Draw the figure and label it with the given information. | 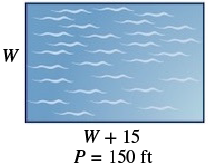 |
| Step 2. Identify what you are looking for. | the length and width of the pool |
| Step 3. Name. Choose a variable to represent it. The length is 15 feet more than the width. |
Let |
| Step 4.Translate. Write the appropriate formula and substitute. |
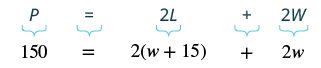 |
| Step 5. Solve the equation. | 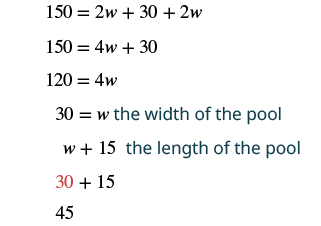 |
| Step 6. Check: | 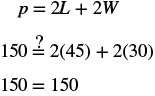 |
| Step 7. Answer the question. | The length of the pool is 45 feet and the width is 30 feet. |
TRY IT 8.1
The perimeter of a rectangular swimming pool is ![]() feet. The length is
feet. The length is ![]() feet more than the width. Find the length and width.
feet more than the width. Find the length and width.
Show answer
30 ft, 70 ft
TRY IT 8.2
The length of a rectangular garden is ![]() yards more than the width. The perimeter is
yards more than the width. The perimeter is ![]() yards. Find the length and width.
yards. Find the length and width.
Show answer
60 yd, 90 yd
Use the Properties of Triangles
We now know how to find the area of a rectangle. We can use this fact to help us visualize the formula for the area of a triangle. In the rectangle in (Figure.9), we’ve labeled the length ![]() and the width
and the width ![]() , so it’s area is
, so it’s area is ![]() .
.
The area of a rectangle is the base, ![]() , times the height,
, times the height, ![]() .
.
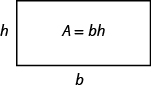
We can divide this rectangle into two congruent triangles (Figure.10). Triangles that are congruent have identical side lengths and angles, and so their areas are equal. The area of each triangle is one-half the area of the rectangle, or ![]() . This example helps us see why the formula for the area of a triangle is
. This example helps us see why the formula for the area of a triangle is ![]() .
.
A rectangle can be divided into two triangles of equal area. The area of each triangle is one-half the area of the rectangle.
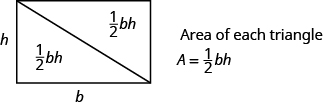
The formula for the area of a triangle is ![]() , where
, where ![]() is the base and
is the base and ![]() is the height.
is the height.
To find the area of the triangle, you need to know its base and height. The base is the length of one side of the triangle, usually the side at the bottom. The height is the length of the line that connects the base to the opposite vertex, and makes a ![]() ° angle with the base. (Figure.11) shows three triangles with the base and height of each marked.
° angle with the base. (Figure.11) shows three triangles with the base and height of each marked.
The height ![]() of a triangle is the length of a line segment that connects the the base to the opposite vertex and makes a
of a triangle is the length of a line segment that connects the the base to the opposite vertex and makes a ![]() ° angle with the base.
° angle with the base.

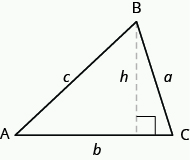
Triangle Properties
For any triangle ![]() , the sum of the measures of the angles is
, the sum of the measures of the angles is ![]() °.
°.
![]() °
°
The perimeter of a triangle is the sum of the lengths of the sides.
![]()
The area of a triangle is one-half the base, ![]() , times the height,
, times the height, ![]() .
.
![]()
EXAMPLE 9
Find the area of a triangle whose base is ![]() inches and whose height is
inches and whose height is ![]() inches.
inches.
| Step 1. Read the problem. Draw the figure and label it with the given information. | 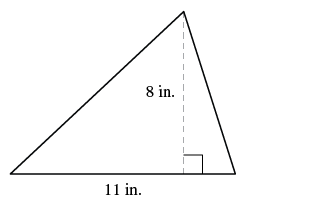 |
| Step 2. Identify what you are looking for. | the area of the triangle |
| Step 3. Name. Choose a variable to represent it. | let A = area of the triangle |
| Step 4.Translate. Write the appropriate formula. Substitute. |
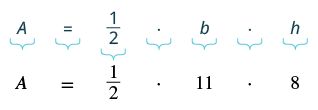 |
| Step 5. Solve the equation. | 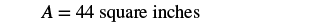 |
| Step 6. Check: | 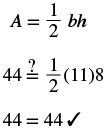 |
| Step 7. Answer the question. | The area is 44 square inches. |
TRY IT 9.1
Find the area of a triangle with base ![]() inches and height
inches and height ![]() inches.
inches.
Show answer
13 sq. in.
TRY IT 9.2
Find the area of a triangle with base ![]() inches and height
inches and height ![]() inches.
inches.
Show answer
49 sq. in.
EXAMPLE 10
The perimeter of a triangular garden is ![]() feet. The lengths of two sides are
feet. The lengths of two sides are ![]() feet and
feet and ![]() feet. How long is the third side?
feet. How long is the third side?
| Step 1. Read the problem. Draw the figure and label it with the given information. | 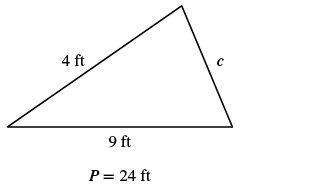 |
| Step 2. Identify what you are looking for. | length of the third side of a triangle |
| Step 3. Name. Choose a variable to represent it. | Let c = the third side |
| Step 4.Translate. Write the appropriate formula. Substitute in the given information. |
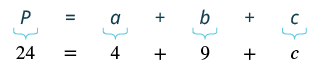 |
| Step 5. Solve the equation. |  |
| Step 6. Check: | 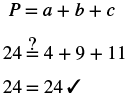 |
| Step 7. Answer the question. | The third side is 11 feet long. |
TRY IT 10.1
The perimeter of a triangular garden is ![]() feet. The lengths of two sides are
feet. The lengths of two sides are ![]() feet and
feet and ![]() feet. How long is the third side?
feet. How long is the third side?
Show answer
8 ft
TRY IT 10.2
The lengths of two sides of a triangular window are ![]() feet and
feet and ![]() feet. The perimeter is
feet. The perimeter is ![]() feet. How long is the third side?
feet. How long is the third side?
Show answer
6 ft
EXAMPLE 11
The area of a triangular church window is ![]() square metres. The base of the window is
square metres. The base of the window is ![]() metres. What is the window’s height?
metres. What is the window’s height?
| Step 1. Read the problem. Draw the figure and label it with the given information. | 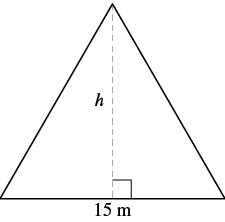 |
| Step 2. Identify what you are looking for. | height of a triangle |
| Step 3. Name. Choose a variable to represent it. | Let h = the height |
| Step 4.Translate. Write the appropriate formula. Substitute in the given information. |
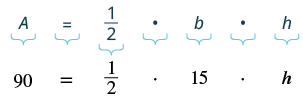 |
| Step 5. Solve the equation. |  |
| Step 6. Check: | 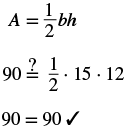 |
| Step 7. Answer the question. | The height of the triangle is 12 metres. |
TRY IT 11.1
The area of a triangular painting is ![]() square inches. The base is
square inches. The base is ![]() inches. What is the height?
inches. What is the height?
Show answer
14 in.
TRY IT 11.2
A triangular tent door has an area of ![]() square feet. The height is
square feet. The height is ![]() feet. What is the base?
feet. What is the base?
Show answer
6 ft
Isosceles and Equilateral Triangles
Besides the right triangle, some other triangles have special names. A triangle with two sides of equal length is called an isosceles triangle. A triangle that has three sides of equal length is called an equilateral triangle. (Figure.12) shows both types of triangles.
In an isosceles triangle, two sides have the same length, and the third side is the base. In an equilateral triangle, all three sides have the same length.
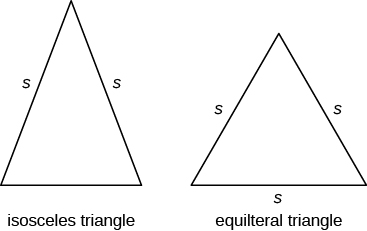
Isosceles and Equilateral Triangles
An isosceles triangle has two sides the same length.
An equilateral triangle has three sides of equal length.
EXAMPLE 12
The perimeter of an equilateral triangle is ![]() inches. Find the length of each side.
inches. Find the length of each side.
| Step 1. Read the problem. Draw the figure and label it with the given information. | 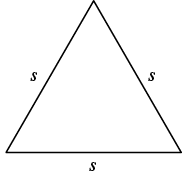 Perimeter = 93 in. |
| Step 2. Identify what you are looking for. | length of the sides of an equilateral triangle |
| Step 3. Name. Choose a variable to represent it. | Let s = length of each side |
| Step 4.Translate. Write the appropriate formula. Substitute. |
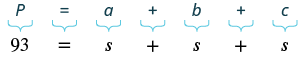 |
| Step 5. Solve the equation. |  |
| Step 6. Check: | 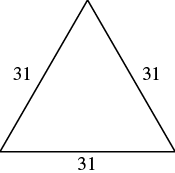
|
| Step 7. Answer the question. | Each side is 31 inches |
TRY IT 12.1
Find the length of each side of an equilateral triangle with perimeter ![]() inches.
inches.
Show answer
13 in.
TRY IT 12.2
Find the length of each side of an equilateral triangle with perimeter ![]() centimetres.
centimetres.
Show answer
17 cm
EXAMPLE 13
Arianna has ![]() inches of beading to use as trim around a scarf. The scarf will be an isosceles triangle with a base of
inches of beading to use as trim around a scarf. The scarf will be an isosceles triangle with a base of ![]() inches. How long can she make the two equal sides?
inches. How long can she make the two equal sides?
| Step 1. Read the problem. Draw the figure and label it with the given information. | 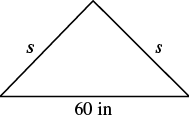 P = 156 in. |
| Step 2. Identify what you are looking for. | the lengths of the two equal sides |
| Step 3. Name. Choose a variable to represent it. | Let s = the length of each side |
| Step 4.Translate. Write the appropriate formula. Substitute in the given information. |
 |
| Step 5. Solve the equation. | 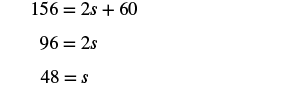 |
| Step 6. Check: | 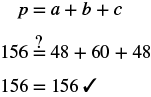 |
| Step 7. Answer the question. | Arianna can make each of the two equal sides 48 inches l |
TRY IT 13.1
A backyard deck is in the shape of an isosceles triangle with a base of ![]() feet. The perimeter of the deck is
feet. The perimeter of the deck is ![]() feet. How long is each of the equal sides of the deck?
feet. How long is each of the equal sides of the deck?
Show answer
14 ft
TRY IT 13.2
A boat’s sail is an isosceles triangle with base of ![]() metres. The perimeter is
metres. The perimeter is ![]() metres. How long is each of the equal sides of the sail?
metres. How long is each of the equal sides of the sail?
Show answer
7 m
Use the Properties of Trapezoids
A trapezoid is four-sided figure, a quadrilateral, with two sides that are parallel and two sides that are not. The parallel sides are called the bases. We call the length of the smaller base ![]() , and the length of the bigger base
, and the length of the bigger base ![]() . The height,
. The height, ![]() , of a trapezoid is the distance between the two bases as shown in (Figure.13).
, of a trapezoid is the distance between the two bases as shown in (Figure.13).
A trapezoid has a larger base, ![]() , and a smaller base,
, and a smaller base, ![]() . The height
. The height ![]() is the distance between the bases.
is the distance between the bases.
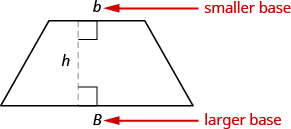
Formula for the Area of a Trapezoid
![]()
Splitting the trapezoid into two triangles may help us understand the formula. The area of the trapezoid is the sum of the areas of the two triangles. See (Figure.14).
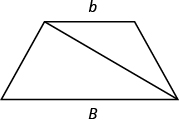
The height of the trapezoid is also the height of each of the two triangles. See (Figure.15).
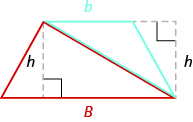
The formula for the area of a trapezoid is
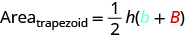
If we distribute, we get,
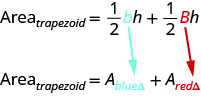
Properties of Trapezoids
- A trapezoid has four sides. See (Figure.13).
- Two of its sides are parallel and two sides are not.
- The area,
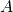 , of a trapezoid is
, of a trapezoid is 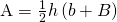 .
.
EXAMPLE 14
Find the area of a trapezoid whose height is 6 inches and whose bases are ![]() and
and ![]() inches.
inches.
| Step 1. Read the problem. Draw the figure and label it with the given information. | 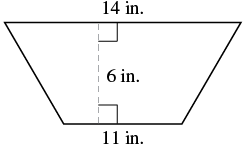 |
| Step 2. Identify what you are looking for. | the area of the trapezoid |
| Step 3. Name. Choose a variable to represent it. | Let |
| Step 4.Translate. Write the appropriate formula. Substitute. |
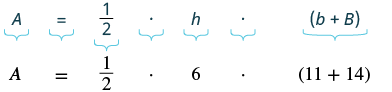 |
| Step 5. Solve the equation. | 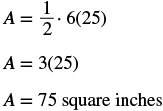 |
| Step 6. Check: Is this answer reasonable? |
If we draw a rectangle around the trapezoid that has the same big base ![]() and a height
and a height ![]() , its area should be greater than that of the trapezoid.
, its area should be greater than that of the trapezoid.
If we draw a rectangle inside the trapezoid that has the same little base ![]() and a height
and a height ![]() , its area should be smaller than that of the trapezoid.
, its area should be smaller than that of the trapezoid.
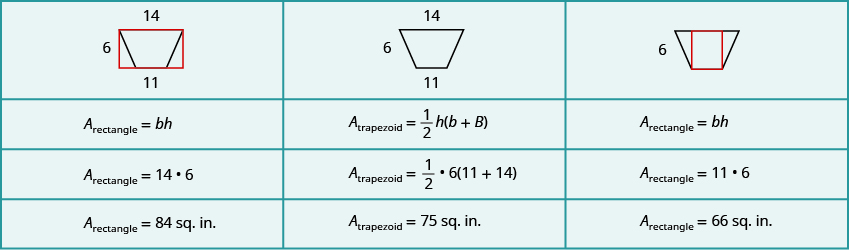
The area of the larger rectangle is ![]() square inches and the area of the smaller rectangle is
square inches and the area of the smaller rectangle is ![]() square inches. So it makes sense that the area of the trapezoid is between
square inches. So it makes sense that the area of the trapezoid is between ![]() and
and ![]() square inches
square inches
Step 7. Answer the question. The area of the trapezoid is ![]() square inches.
square inches.
TRY IT 14.1
The height of a trapezoid is ![]() yards and the bases are
yards and the bases are ![]() and
and ![]() yards. What is the area?
yards. What is the area?
Show answer
161 sq. yd
TRY IT 14.2
The height of a trapezoid is ![]() centimetres and the bases are
centimetres and the bases are ![]() and
and ![]() centimetres. What is the area?
centimetres. What is the area?
Show answer
225 sq. cm
EXAMPLE 15
Find the area of a trapezoid whose height is ![]() feet and whose bases are
feet and whose bases are ![]() and
and ![]() feet.
feet.
| Step 1. Read the problem. Draw the figure and label it with the given information. | 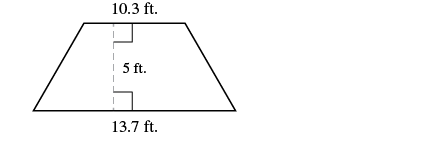 |
| Step 2. Identify what you are looking for. | the area of the trapezoid |
| Step 3. Name. Choose a variable to represent it. | Let A = the area |
| Step 4.Translate. Write the appropriate formula. Substitute. |
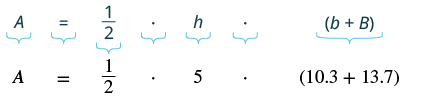 |
| Step 5. Solve the equation. |  |
| Step 6. Check: Is this answer reasonable? The area of the trapezoid should be less than the area of a rectangle with base 13.7 and height 5, but more than the area of a rectangle with base 10.3 and height 5. |
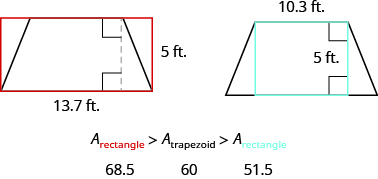 |
| Step 7. Answer the question. | The area of the trapezoid is 60 square feet. |
TRY IT 15.1
The height of a trapezoid is ![]() centimetres and the bases are
centimetres and the bases are ![]() and
and ![]() centimetres. What is the area?
centimetres. What is the area?
Show answer
42 sq. cm
TRY IT 15.2
The height of a trapezoid is ![]() metres and the bases are
metres and the bases are ![]() and
and ![]() metres. What is the area?
metres. What is the area?
Show answer
63 sq. m
EXAMPLE 16
Vinny has a garden that is shaped like a trapezoid. The trapezoid has a height of ![]() yards and the bases are
yards and the bases are ![]() and
and ![]() yards. How many square yards will be available to plant?
yards. How many square yards will be available to plant?
| Step 1. Read the problem. Draw the figure and label it with the given information. | 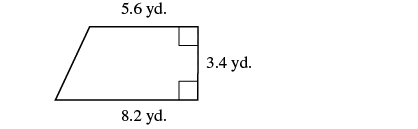 |
| Step 2. Identify what you are looking for. | the area of a trapezoid |
| Step 3. Name. Choose a variable to represent it. | Let A = the area |
| Step 4.Translate. Write the appropriate formula. Substitute. |
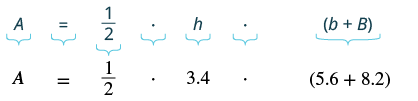 |
| Step 5. Solve the equation. |  |
| Step 6. Check: Is this answer reasonable? Yes. The area of the trapezoid is less than the area of a rectangle with a base of 8.2 yd and height 3.4 yd, but more than the area of a rectangle with base 5.6 yd and height 3.4 yd.  |
|
| Step 7. Answer the question. | Vinny has 23.46 square yards in which he can plan |
TRY IT 16.1
Lin wants to sod his lawn, which is shaped like a trapezoid. The bases are ![]() yards and
yards and ![]() yards, and the height is
yards, and the height is ![]() yards. How many square yards of sod does he need?
yards. How many square yards of sod does he need?
Show answer
40.25 sq. yd
TRY IT 16.2
Kira wants cover his patio with concrete pavers. If the patio is shaped like a trapezoid whose bases are ![]() feet and
feet and ![]() feet and whose height is
feet and whose height is ![]() feet, how many square feet of pavers will he need?
feet, how many square feet of pavers will he need?
Show answer
240 sq. ft.
Access Additional Online Resources
Key Concepts
- Properties of Rectangles
- Rectangles have four sides and four right (90°) angles.
- The lengths of opposite sides are equal.
- The perimeter,
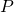 , of a rectangle is the sum of twice the length and twice the width.
, of a rectangle is the sum of twice the length and twice the width.
- The area,
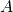 , of a rectangle is the length times the width.
, of a rectangle is the length times the width.
- Triangle Properties
- For any triangle
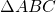 , the sum of the measures of the angles is 180°.
, the sum of the measures of the angles is 180°.
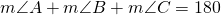 °
°
- The perimeter of a triangle is the sum of the lengths of the sides.
- The area of a triangle is one-half the base, b, times the height, h.
- For any triangle
Glossary
- area
- The area is a measure of the surface covered by a figure.
- equilateral triangle
- A triangle with all three sides of equal length is called an equilateral triangle.
- isosceles triangle
- A triangle with two sides of equal length is called an isosceles triangle.
- perimeter
- The perimeter is a measure of the distance around a figure.
- rectangle
- A rectangle is a geometric figure that has four sides and four right angles.
- trapezoid
- A trapezoid is four-sided figure, a quadrilateral, with two sides that are parallel and two sides that are not.
Practice Makes Perfect
Understand Linear, Square, and Cubic Measure
In the following exercises, determine whether you would measure each item using linear, square, or cubic units.
| 1. amount of water in a fish tank | 2. length of dental floss |
| 3. living area of an apartment | 4. floor space of a bathroom tile |
| 5. height of a doorway | 6. capacity of a truck trailer |
In the following exercises, find the a) perimeter and b) area of each figure. Assume each side of the square is ![]() cm.
cm.
7.  |
8.  |
9.  |
10.  |
11.  |
12. 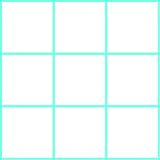 |
Use the Properties of Rectangles
In the following exercises, find the a) perimeter and b) area of each rectangle.
| 13. The length of a rectangle is |
14. The length of a rectangle is |
| 15. A rectangular room is |
16. A driveway is in the shape of a rectangle |
In the following exercises, solve.
| 17. Find the length of a rectangle with perimeter |
18. Find the length of a rectangle with perimeter |
| 19. Find the width of a rectangle with perimeter |
20. Find the width of a rectangle with perimeter |
| 21. The area of a rectangle is |
22. The area of a rectangle is |
| 23. The length of a rectangle is |
24. The width of a rectangle is |
| 25. The perimeter of a rectangle is |
26. The perimeter of a rectangle is |
| 27. The width of the rectangle is |
28. The length of the rectangle is |
| 29. The perimeter of a rectangle of |
30. The length of a rectangle is three times the width. The perimeter is |
| 31. The length of a rectangle is |
32. The length of a rectangle is |
| 33. The width of a rectangular window is |
34. The length of a rectangular poster is |
| 35. The area of a rectangular roof is |
36. The area of a rectangular tarp is |
| 37. The perimeter of a rectangular courtyard is |
38. The perimeter of a rectangular painting is |
| 39. The width of a rectangular window is |
40. The width of a rectangular playground is |
Use the Properties of Triangles
In the following exercises, solve using the properties of triangles.
| 41. Find the area of a triangle with base |
42. Find the area of a triangle with base |
| 43. Find the area of a triangle with base |
44. Find the area of a triangle with base |
| 45. A triangular flag has base of |
46. A triangular window has base of |
| 47. If a triangle has sides of |
48. If a triangle has sides of |
| 49. What is the base of a triangle with an area of |
50. What is the height of a triangle with an area of |
| 51. The perimeter of a triangular reflecting pool is |
52. A triangular courtyard has perimeter of |
| 53. An isosceles triangle has a base of |
54. An isosceles triangle has a base of |
| 55. Find the length of each side of an equilateral triangle with a perimeter of |
56. Find the length of each side of an equilateral triangle with a perimeter of |
| 57. The perimeter of an equilateral triangle is |
58. The perimeter of an equilateral triangle is |
| 59. The perimeter of an isosceles triangle is |
60. The perimeter of an isosceles triangle is |
| 61. A dish is in the shape of an equilateral triangle. Each side is |
62. A floor tile is in the shape of an equilateral triangle. Each side is |
| 63. A road sign in the shape of an isosceles triangle has a base of |
64. A scarf in the shape of an isosceles triangle has a base of |
| 65. The perimeter of a triangle is |
66. The perimeter of a triangle is |
| 67. One side of a triangle is twice the smallest side. The third side is |
68. One side of a triangle is three times the smallest side. The third side is |
Use the Properties of Trapezoids
In the following exercises, solve using the properties of trapezoids.
| 69. The height of a trapezoid is |
70. The height of a trapezoid is |
| 71. Find the area of a trapezoid with a height of |
72. Find the area of a trapezoid with a height of |
| 73. The height of a trapezoid is |
74. The height of a trapezoid is |
| 75. Find the area of a trapezoid with a height of |
76. Find the area of a trapezoid with a height of |
| 77. Laurel is making a banner shaped like a trapezoid. The height of the banner is |
78. Niko wants to tile the floor of his bathroom. The floor is shaped like a trapezoid with width |
| 79. Theresa needs a new top for her kitchen counter. The counter is shaped like a trapezoid with width |
80. Elena is knitting a scarf. The scarf will be shaped like a trapezoid with width |
Everyday Math
| 81. Fence Jose just removed the children’s playset from his back yard to make room for a rectangular garden. He wants to put a fence around the garden to keep out the dog. He has a |
82. Gardening Lupita wants to fence in her tomato garden. The garden is rectangular and the length is twice the width. It will take |
| 83. Fence Christa wants to put a fence around her triangular flowerbed. The sides of the flowerbed are |
84. Painting Caleb wants to paint one wall of his attic. The wall is shaped like a trapezoid with height
|
Writing Exercises
| 86. If you need to put a fence around your backyard, do you need to know the perimeter or the area of the backyard? Explain your reasoning. | |
|
87. Look at the two figures.
a) Which figure looks like it has the larger area? Which looks like it has the larger perimeter? b) Now calculate the area and perimeter of each figure. Which has the larger area? Which has the larger perimeter? |
88. The length of a rectangle is a) Write the equation you would use to solve the problem. b) Why can’t you solve this equation with the methods you learned in the previous chapter? |
Answers
| 1. cubic | 3. square | 5. linear |
| 7.
a) 10 cm b) 4 sq. cm |
9.
a) 8 cm b) 3 sq. cm |
11.
a) 10 cm b) 5 sq. cm |
| 13.
a) 260 ft b) 3825 sq. ft |
15.
a) 58 ft b) 210 sq. ft |
17. 24 inches |
| 19. 27 metres | 21. 23 m | 23. 7 in., 16 in. |
| 25. 17 m, 12 m | 27. 13.5 m, 12.8 m | 29. 25 ft, 50 ft |
| 31. 7 m, 11 m | 33. 26 in. | 35. 55 m |
| 37. 35 ft, 45 ft | 39. 76 in., 36 in. | 41. 60 sq. in. |
| 43. 25.315 sq. m | 45. 0.75 sq. ft | 47. 8 ft |
| 49. 23 in. | 51. 11 ft | 53. 28 cm |
| 55. 17 ft | 57. 6 m | 59. 15 ft |
| 61. 24 in. | 63. 27.5 in. | 65. 12 ft, 13 ft, 14 ft |
| 67. 3 ft, 6 ft, 8 ft | 69. 144 sq. ft | 71. 2805 sq. m |
| 73. 231 sq. cm | 75. 28.56 sq. m | 77. 13.5 sq. ft |
| 79. 1036 sq. in. | 81. 15 ft | 83. $24 |
| 85. Answers will vary. | 87. Answers will vary. |
Attributions
This chapter has been adapted from “Use Properties of Rectangles, Triangles, and Trapezoids” in Prealgebra (OpenStax) by Lynn Marecek, MaryAnne Anthony-Smith, and Andrea Honeycutt Mathis, which is under a CC BY 4.0 Licence. Adapted by Izabela Mazur. See the Copyright page for more information.