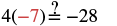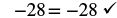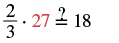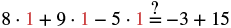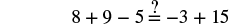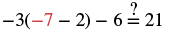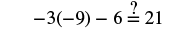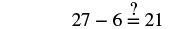CHAPTER 5 Solving First Degree Equations in One Variable
5.2 Solve Equations Using the Division and Multiplication Properties of Equality
Learning Objectives
By the end of this section, you will be able to:
- Solve equations using the Division and Multiplication Properties of Equality
- Solve equations that need to be simplified
Solve Equations Using the Division and Multiplication Properties of Equality
You may have noticed that all of the equations we have solved so far have been of the form ![]() or
or ![]() . We were able to isolate the variable by adding or subtracting the constant term on the side of the equation with the variable. Now we will see how to solve equations that have a variable multiplied by a constant and so will require division to isolate the variable.
. We were able to isolate the variable by adding or subtracting the constant term on the side of the equation with the variable. Now we will see how to solve equations that have a variable multiplied by a constant and so will require division to isolate the variable.
Let’s look at our puzzle again with the envelopes and counters in (Figure 1).
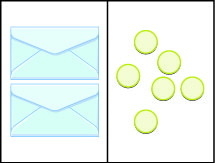
In the illustration there are two identical envelopes that contain the same number of counters. Remember, the left side of the workspace must equal the right side, but the counters on the left side are “hidden” in the envelopes. So how many counters are in each envelope?
How do we determine the number? We have to separate the counters on the right side into two groups of the same size to correspond with the two envelopes on the left side. The 6 counters divided into 2 equal groups gives 3 counters in each group (since ![]() ).
).
What equation models the situation shown in (Figure 2)? There are two envelopes, and each contains ![]() counters. Together, the two envelopes must contain a total of 6 counters.
counters. Together, the two envelopes must contain a total of 6 counters.
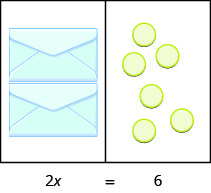
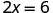 |
|
| If we divide both sides of the equation by 2, as we did with the envelopes and counters, | 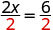 |
| we get: | 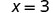 |
We found that each envelope contains 3 counters. Does this check? We know ![]() , so it works! Three counters in each of two envelopes does equal six!
, so it works! Three counters in each of two envelopes does equal six!
This example leads to the Division Property of Equality.
Division and Multiplication Properties of Equality
Division Property of Equality: For all real numbers ![]() , and
, and ![]() , if
, if ![]() , then
, then ![]() .
.
Multiplication Property of Equality: For all real numbers ![]() , if
, if ![]() , then
, then ![]() .
.
When you divide or multiply both sides of an equation by the same quantity, you still have equality.
Let’s review how these properties of equality can be applied in order to solve equations. Remember, the goal is to ‘undo’ the operation on the variable. In the example below the variable is multiplied by ![]() , so we will divide both sides by
, so we will divide both sides by ![]() to ‘undo’ the multiplication.
to ‘undo’ the multiplication.
EXAMPLE 1
Solve: ![]() .
.
Solution
We use the Division Property of Equality to divide both sides by ![]() .
.
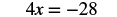 |
|
| Divide both sides by 4 to undo the multiplication. | 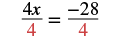 |
| Simplify. | 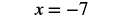 |
| Check your answer. Let |
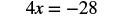
|
Since this is a true statement, ![]() is a solution to
is a solution to ![]() .
.
TRY IT 1.1
Solve: ![]() .
.
Show answer
y = −16
TRY IT 1.2
Solve: ![]() .
.
Show answer
z = −13
In the previous example, to ‘undo’ multiplication, we divided. How do you think we ‘undo’ division?
EXAMPLE 2
Solve: ![]() .
.
Solution
Here ![]() is divided by
is divided by ![]() . We can multiply both sides by
. We can multiply both sides by ![]() to isolate
to isolate ![]() .
.
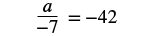 |
|
| Multiply both sides by |
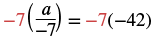 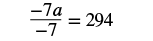 |
| Simplify. | 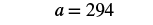 |
| Check your answer. Let |
|
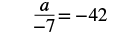 |
|
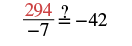 |
|
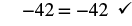 |
TRY IT 2.1
Solve: ![]() .
.
Show answer
b = 144
TRY IT 2.2
Solve: ![]() .
.
Show answer
c = 128
EXAMPLE 3
Solve: ![]() .
.
Solution
Remember ![]() is equivalent to
is equivalent to ![]() .
.
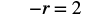 |
||
| Rewrite |
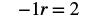 |
|
| Divide both sides by |
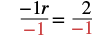 |
|
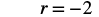 |
||
| Check. | 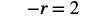 |
|
| Substitute |
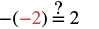 |
|
| Simplify. | 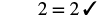 |
|
We see that there are two other ways to solve ![]() .
.
We could multiply both sides by ![]() .
.
We could take the opposite of both sides.
TRY IT 3.1
Solve: ![]() .
.
Show answer
k = −8
TRY IT 3.2
Solve: ![]() .
.
Show answer
g = −3
EXAMPLE 4
Solve: ![]() .
.
Solution
Since the product of a number and its reciprocal is ![]() , our strategy will be to isolate
, our strategy will be to isolate ![]() by multiplying by the reciprocal of
by multiplying by the reciprocal of ![]() .
.
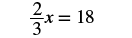 |
|
| Multiply by the reciprocal of |
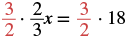 |
| Reciprocals multiply to one. | 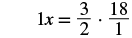 |
| Multiply. | 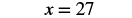 |
| Check your answer. Let |
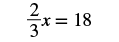
|
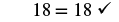 |
Notice that we could have divided both sides of the equation ![]() by
by ![]() to isolate
to isolate ![]() . While this would work, multiplying by the reciprocal requires fewer steps.
. While this would work, multiplying by the reciprocal requires fewer steps.
TRY IT 4.1
Solve: ![]() .
.
Show answer
n = 35
TRY IT 4.2
Solve: ![]() .
.
Show answer
y = 18
Solve Equations That Need to be Simplified
Many equations start out more complicated than the ones we’ve just solved. First, we need to simplify both sides of the equation as much as possible
EXAMPLE 5
Solve: ![]() .
.
Solution
Start by combining like terms to simplify each side.
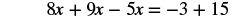 |
|
| Combine like terms. | 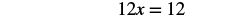 |
| Divide both sides by 12 to isolate x. | 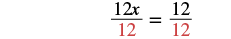 |
| Simplify. |  |
| Check your answer. Let |
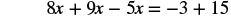
|
TRY IT 5.1
Solve: ![]() .
.
Show answer
x = 2
TRY IT 5.2
Solve: ![]() .
.
Show answer
n = −5
EXAMPLE 6
Solve: ![]() .
.
Solution
Simplify each side by combining like terms.
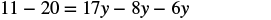 |
|
| Simplify each side. |  |
| Divide both sides by 3 to isolate y. |  |
| Simplify. |  |
| Check your answer. Let |
|
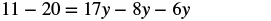 |
|
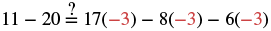 |
|
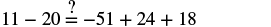 |
|
 |
Notice that the variable ended up on the right side of the equal sign when we solved the equation. You may prefer to take one more step to write the solution with the variable on the left side of the equal sign.
TRY IT 6.1
Solve: ![]() .
.
Show answer
c = −3
TRY IT 6.2
Solve: ![]() .
.
Show answer
![]()
EXAMPLE 7
Solve: ![]() .
.
Solution
Remember—always simplify each side first.
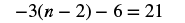 |
|
| Distribute. | 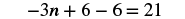 |
| Simplify. | 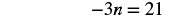 |
| Divide both sides by -3 to isolate n. | 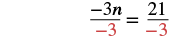  |
| Check your answer. Let |
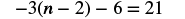
|
TRY IT 7.1
Solve: ![]() .
.
Show answer
n = −6
TRY IT 7.2
Solve: ![]() .
.
Show answer
n = −5
Key Concepts
- Division and Multiplication Properties of Equality
- Division Property of Equality: For all real numbers a, b, c, and
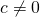 , if
, if 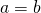 , then
, then 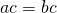 .
. - Multiplication Property of Equality: For all real numbers a, b, c, if
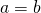 , then
, then 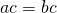 .
.
- Division Property of Equality: For all real numbers a, b, c, and
Practice Makes Perfect
Solve Equations Using the Division and Multiplication Properties of Equality
In the following exercises, solve each equation for the variable using the Division Property of Equality and check the solution.
| 1. |
2. |
| 3. |
4. |
| 5. |
6. |
| 7. |
8. |
| 9. |
10. |
| 11. |
12. |
In the following exercises, solve each equation for the variable using the Multiplication Property of Equality and check the solution.
| 13. |
14. |
| 15. |
16. |
| 17. |
18. |
| 19. |
20. |
| 21. |
22. |
| 23. |
24. |
| 25. |
26. |
Solve Equations That Need to be Simplified
In the following exercises, solve the equation.
| 27. |
28. |
| 29. |
30. |
| 31. |
32. |
| 33. |
34. |
| 35. |
36. |
Everyday Math
| 37. Teaching Connie’s kindergarten class has |
38. Balloons Ramona bought |
| 39. Unit price Nishant paid |
40. Ticket price Daria paid |
| 41. Fabric The drill team used |
42. Fuel economy Tania’s SUV gets half as many miles per gallon (mpg) as her husband’s hybrid car. The SUV gets |
Writing Exercises
| 43. Emiliano thinks |
44. Frida started to solve the equation |
Answers
| 1. 9 | 3. 3 | 5. −6 |
| 7. 7 | 9. 15 | 11. 0 |
| 13. 28 | 15. 36 | 17. −48 |
| 19. 80 | 21. 25 | 23. −32 |
| 25. 5/2 | 27. y = −1 | 29. m = −5 |
| 31. |
33. q = 24 | 35. p = 56 |
| 37. 6 children | 39. $1.08 | 41. 42 yards |
| 43. Answer will vary. |
Attributions
This chapter has been adapted from “Solve Equations Using the Division and Multiplication Properties of Equality” in Prealgebra (OpenStax) by Lynn Marecek, MaryAnne Anthony-Smith, and Andrea Honeycutt Mathis, which is under a CC BY 4.0 Licence. Adapted by Izabela Mazur. See the Copyright page for more information.