CHAPTER 8 Polynomials
8.1 Add and Subtract Polynomials
Learning Objectives
By the end of this section, you will be able to:
- Identify polynomials, monomials, binomials, and trinomials
- Determine the degree of polynomials
- Add and subtract monomials
- Add and subtract polynomials
- Evaluate a polynomial for a given value
Identify Polynomials, Monomials, Binomials and Trinomials
You have learned that a term is a constant or the product of a constant and one or more variables. When it is of the form ![]() , where
, where ![]() is a constant and
is a constant and ![]() is a whole number, it is called a monomial. Some examples of monomial are
is a whole number, it is called a monomial. Some examples of monomial are ![]() , and
, and ![]() .
.
Monomials
A monomial is a term of the form ![]() , where
, where ![]() is a constant and
is a constant and ![]() is a positive whole number.
is a positive whole number.
A monomial, or two or more monomials combined by addition or subtraction, is a polynomial. Some polynomials have special names, based on the number of terms. A monomial is a polynomial with exactly one term. A binomial has exactly two terms, and a trinomial has exactly three terms. There are no special names for polynomials with more than three terms.
Polynomials
polynomial—A monomial, or two or more monomials combined by addition or subtraction, is a polynomial.
- monomial—A polynomial with exactly one term is called a monomial.
- binomial—A polynomial with exactly two terms is called a binomial.
- trinomial—A polynomial with exactly three terms is called a trinomial.
Here are some examples of polynomials.
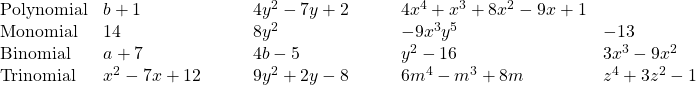
Notice that every monomial, binomial, and trinomial is also a polynomial. They are just special members of the “family” of polynomials and so they have special names. We use the words monomial, binomial, and trinomial when referring to these special polynomials and just call all the rest polynomials.
EXAMPLE 1
Determine whether each polynomial is a monomial, binomial, trinomial, or other polynomial.
| Polynomial | Number of terms | Type | |
| a) | Trinomial | ||
| b) | Monomial | ||
| c) | Polynomial | ||
| d) | Binomial | ||
| e) | Monomial |
TRY IT 1.1
Determine whether each polynomial is a monomial, binomial, trinomial, or other polynomial:
a) ![]() b)
b) ![]() c)
c) ![]() d)
d) ![]() e)
e)![]()
Show answer
a) monomial b) polynomial c) trinomial d) binomial e) monomial
TRY IT 1.2
Determine whether each polynomial is a monomial, binomial, trinomial, or other polynomial:
a) ![]() b)
b) ![]() c)
c) ![]() d)
d) ![]() e)
e) ![]()
Show answer
a) binomial b) trinomial c) monomial d) polynomial e) monomial
Determine the Degree of Polynomials
The degree of a polynomial and the degree of its terms are determined by the exponents of the variable.
A monomial that has no variable, just a constant, is a special case. The degree of a constant is 0—it has no variable.
Degree of a Polynomial
The degree of a term is the sum of the exponents of its variables.
The degree of a constant is 0.
The degree of a polynomial is the highest degree of all its terms.
Let’s see how this works by looking at several polynomials. We’ll take it step by step, starting with monomials, and then progressing to polynomials with more terms.

A polynomial is in standard form when the terms of a polynomial are written in descending order of degrees. Get in the habit of writing the term with the highest degree first.
EXAMPLE 2
Find the degree of the following polynomials.
| a) The exponent of |
The degree is 1. |
| b) The highest degree of all the terms is 3. |
The degree is 3. |
| c) The degree of a constant is 0. |
The degree is 0. |
| d) The highest degree of all the terms is 2. |
The degree is 2. |
| e) The highest degree of all the terms is 3. |
The degree is 3. |
EXAMPLE 2.1
Find the degree of the following polynomials:
a) ![]() b)
b) ![]() c)
c) ![]() d)
d) ![]() e)
e)![]()
Show answer
a) ![]() b)
b) ![]() c)
c) ![]() d) 3 e) 0
d) 3 e) 0
TRY IT 2.2
Find the degree of the following polynomials:
a) ![]() b)
b) ![]() c)
c) ![]() d)
d) ![]() e)
e)![]()
Show answer
a) ![]() b)
b) ![]() c)
c) ![]() d) 2 e) 3
d) 2 e) 3
Add and Subtract Monomials
You have learned how to simplify expressions by combining like terms. Remember, like terms must have the same variables with the same exponent. Since monomials are terms, adding and subtracting monomials is the same as combining like terms. If the monomials are like terms, we just combine them by adding or subtracting the coefficient.
EXAMPLE 3
Add: ![]() .
.
| Combine like terms. |
TRY IT 3.1
Add: ![]() .
.
Show answer
![]()
TRY 3.2
Add: ![]() .
.
Show answer
![]()
EXAMPLE 4
Subtract: ![]() .
.
| Combine like terms. |
TRY IT 4.1
Subtract: ![]() .
.
Show answer
![]()
TRY IT 4.2
Subtract: ![]() .
.
Show answer
![]()
Remember that like terms must have the same variables with the same exponents.
EXAMPLE 5
Simplify: ![]() .
.
| Combine like terms. |
TRY IT 5.1
Add: ![]() .
.
Show answer
![]()
TRY IT 5.2
Add: ![]() .
.
Show answer
![]()
EXAMPLE 6
Simplify: ![]() .
.
| There are no like terms to combine. |
TRY IT 6.1
Simplify: ![]() .
.
Show answer
There are no like terms to combine.
TRY IT 6.2
Simplify: ![]() .
.
Show answer
There are no like terms to combine.
Add and Subtract Polynomials
We can think of adding and subtracting polynomials as just adding and subtracting a series of monomials. Look for the like terms—those with the same variables and the same exponent. The Commutative Property allows us to rearrange the terms to put like terms together.
EXAMPLE 7
Find the sum: ![]() .
.
| Identify like terms. | 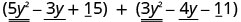 |
| Rearrange to get the like terms together. | 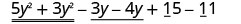 |
| Combine like terms. | 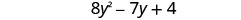 |
TRY IT 7.1
Find the sum: ![]() .
.
Show answer
![]()
TRY IT 7.2
Find the sum: ![]() .
.
Show answer
![]()
EXAMPLE 8
Find the difference: ![]() .
.
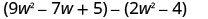 |
|
| Distribute and identify like terms. | 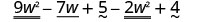 |
| Rearrange the terms. | 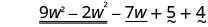 |
| Combine like terms. | 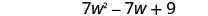 |
TRY IT 8.1
Find the difference: ![]() .
.
Show answer
![]()
TRY IT 8.2
Find the difference: ![]() .
.
Show answer
![]()
EXAMPLE 9
Subtract: ![]() from
from ![]() .
.
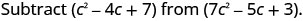 |
|
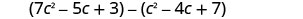 |
|
| Distribute and identify like terms. | 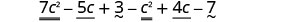 |
| Rearrange the terms. | 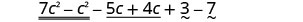 |
| Combine like terms. | 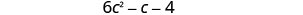 |
TRY IT 9.1
Subtract: ![]() from
from ![]() .
.
Show answer
![]()
TRY IT 9.2
Subtract: ![]() from
from ![]() .
.
Show answer
![]()
EXAMPLE 10
Find the sum: ![]() .
.
| Distribute. | |
| Rearrange the terms, to put like terms together. | |
| Combine like terms. |
EXAMPLE 10.1
Find the sum: ![]() .
.
Show answer
![]()
EXAMPLE 10.2
Find the sum: ![]() .
.
Show answer
![]()
EXAMPLE 11.1
Find the difference: ![]() .
.
| Distribute. | |
| Rearrange the terms, to put like terms together. | |
| Combine like terms. |
TRY IT 11.1
Find the difference: ![]() .
.
Show answer
![]()
TRY IT 11.2
Find the difference: ![]() .
.
Show answer
![]()
EXAMPLE 12
Simplify: ![]() .
.
| Distribute. | |
| Rearrange the terms, to put like terms together. | |
| Combine like terms. |
TRY IT 12.1
Simplify: ![]() .
.
Show answer
![]()
TRY IT 12.2
Simplify: ![]() .
.
Show answer
![]()
Evaluate a Polynomial for a Given Value
We have already learned how to evaluate expressions. Since polynomials are expressions, we’ll follow the same procedures to evaluate a polynomial. We will substitute the given value for the variable and then simplify using the order of operations.
EXAMPLE 13
Evaluate ![]() when
when
| a) |
|
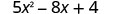 |
|
 |
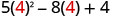 |
| Simplify the exponents. | 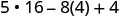 |
| Multiply. | 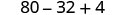 |
| Simplify. | 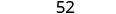 |
| b) |
|
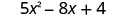 |
|
 |
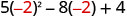 |
| Simplify the exponents. | 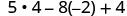 |
| Multiply. | 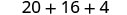 |
| Simplify. | 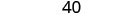 |
| c) |
|
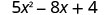 |
|
 |
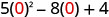 |
| Simplify the exponents. | 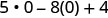 |
| Multiply. | 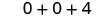 |
| Simplify. | 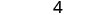 |
TRY IT 13.1
Evaluate: ![]() when
when
Show answer
a) ![]() b)
b) ![]() c)
c) ![]()
TRY IT 13.2
Evaluate: ![]() when
when
Show answer
a) ![]() b)
b) ![]() c)
c) ![]()
EXAMPLE 14
The polynomial ![]() gives the height of a ball
gives the height of a ball ![]() seconds after it is dropped from a 250 foot tall building. Find the height after
seconds after it is dropped from a 250 foot tall building. Find the height after ![]() seconds.
seconds.
| Substitute |
|
| Simplify. | |
| Simplify. | |
| Simplify. | |
| After 2 seconds the height of the ball is 186 feet. |
TRY IT 14.1
The polynomial ![]() gives the height of a ball
gives the height of a ball ![]() seconds after it is dropped from a 250-foot tall building. Find the height after
seconds after it is dropped from a 250-foot tall building. Find the height after ![]() seconds.
seconds.
Show answer
![]()
TRY IT 14.2
The polynomial ![]() gives the height of a ball
gives the height of a ball ![]() seconds after it is dropped from a 250-foot tall building. Find the height after
seconds after it is dropped from a 250-foot tall building. Find the height after ![]() seconds.
seconds.
Show answer
![]()
EXAMPLE 15
The polynomial ![]() gives the cost, in dollars, of producing a rectangular container whose top and bottom are squares with side x feet and sides of height y feet. Find the cost of producing a box with
gives the cost, in dollars, of producing a rectangular container whose top and bottom are squares with side x feet and sides of height y feet. Find the cost of producing a box with ![]() feet and
feet and ![]() feet.
feet.
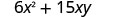 |
|
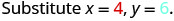 |
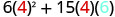 |
| Simplify. | 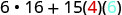 |
| Simplify. | 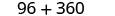 |
| Simplify. | 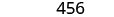 |
| The cost of producing the box is $456. |
TRY IT 15.1
The polynomial ![]() gives the cost, in dollars, of producing a rectangular container whose top and bottom are squares with side x feet and sides of height y feet. Find the cost of producing a box with
gives the cost, in dollars, of producing a rectangular container whose top and bottom are squares with side x feet and sides of height y feet. Find the cost of producing a box with ![]() feet and
feet and ![]() feet.
feet.
Show answer
$576
TRY IT 15.2
The polynomial ![]() gives the cost, in dollars, of producing a rectangular container whose top and bottom are squares with side x feet and sides of height y feet. Find the cost of producing a box with
gives the cost, in dollars, of producing a rectangular container whose top and bottom are squares with side x feet and sides of height y feet. Find the cost of producing a box with ![]() feet and
feet and ![]() feet.
feet.
Show answer
$750
Access these online resources for additional instruction and practice with adding and subtracting polynomials.
Key Concepts
- Monomials
- A monomial is a term of the form
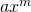 , where
, where  is a constant and
is a constant and 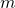 is a whole number
is a whole number
- A monomial is a term of the form
- Polynomials
- polynomial—A monomial, or two or more monomials combined by addition or subtraction is a polynomial.
- monomial—A polynomial with exactly one term is called a monomial.
- binomial—A polynomial with exactly two terms is called a binomial.
- trinomial—A polynomial with exactly three terms is called a trinomial.
- Degree of a Polynomial
- The degree of a term is the sum of the exponents of its variables.
- The degree of a constant is 0.
- The degree of a polynomial is the highest degree of all its terms.
Glossary
- binomial
- A binomial is a polynomial with exactly two terms.
- degree of a constant
- The degree of any constant is 0.
- degree of a polynomial
- The degree of a polynomial is the highest degree of all its terms.
- degree of a term
- The degree of a term is the exponent of its variable.
- monomial
- A monomial is a term of the form
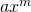 , where
, where  is a constant and
is a constant and 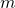 is a whole number; a monomial has exactly one term.
is a whole number; a monomial has exactly one term.
- polynomial
- A polynomial is a monomial, or two or more monomials combined by addition or subtraction.
- standard form
- A polynomial is in standard form when the terms of a polynomial are written in descending order of degrees.
- trinomial
- A trinomial is a polynomial with exactly three terms.
Type your textbox content here.
Practice Makes Perfect
Identify Polynomials, Monomials, Binomials, and Trinomials
In the following exercises, determine if each of the following polynomials is a monomial, binomial, trinomial, or other polynomial.
|
1. a) |
2. a) |
|
3. a) |
4. a) |
Determine the Degree of Polynomials
In the following exercises, determine the degree of each polynomial.
|
5. a) |
6. a) |
|
7. a) |
8. a) |
Add and Subtract Monomials
In the following exercises, add or subtract the monomials.
| 9. |
10. |
| 11. |
12. |
| 13. |
14. |
| 15. |
16. |
| 17. |
18. |
| 19. |
20. |
| 21. |
22. |
| 23. |
24. |
| 25. |
26. |
| 27. |
28. |
| 29. Add: |
30. Add: |
| 31. Subtract |
32. Subtract |
Add and Subtract Polynomials
In the following exercises, add or subtract the polynomials.
| 33. |
34. |
| 35. |
36. |
| 37. |
38. |
| 39. |
40. |
| 41. |
42. |
| 43. |
44. |
| 45. |
46. |
| 47. Subtract |
48. Subtract |
| 49. Subtract |
50. Subtract |
| 51. Find the sum of |
52. Find the sum of |
| 53. Find the sum of |
54. Find the sum of |
| 55. Find the difference of |
56. Find the difference of |
| 57. Find the difference of |
58. Find the difference of |
| 59. |
60. |
| 61. |
62. |
| 63. |
64. |
| 65. |
66. |
| 67. |
68. |
| 69. |
70. |
Evaluate a Polynomial for a Given Value
In the following exercises, evaluate each polynomial for the given value.
|
71. Evaluate a)
|
72. Evaluate a)
|
|
73. Evaluate a) |
74. Evaluate a) |
| 75. A painter drops a brush from a platform 75 feet high. The polynomial |
76. A girl drops a ball off a cliff into the ocean. The polynomial |
| 77. A manufacturer of stereo sound speakers has found that the revenue received from selling the speakers at a cost of p dollars each is given by the polynomial |
78. A manufacturer of the latest basketball shoes has found that the revenue received from selling the shoes at a cost of p dollars each is given by the polynomial |
Everyday Math
| 79. Fuel Efficiency The fuel efficiency (in miles per gallon) of a car going at a speed of |
80. Stopping Distance The number of feet it takes for a car traveling at |
| 81. Rental Cost The cost to rent a rug cleaner for |
82. Height of Projectile The height (in feet) of an object projected upward is given by the polynomial |
| 83. Temperature Conversion The temperature in degrees Fahrenheit is given by the polynomial |
Writing Exercises
| 84. Using your own words, explain the difference between a monomial, a binomial, and a trinomial. | 85. Using your own words, explain the difference between a polynomial with five terms and a polynomial with a degree of 5. |
| 86. Ariana thinks the sum |
87. Jonathan thinks that |
Answers
| 1. a) trinomial b) polynomial c) binomial d) monomial e) binomial | 3. a) binomial b) trinomial c) polynomial d) trinomial e) monomial |
| 5. a) 2 b) 4 c) 1 d) 3 e) 0 | 7. a) 1 b) 2 c) 3 d) 3 e) 0 |
| 9. |
11. |
| 13. |
15. |
| 17. |
19. |
| 21. |
21. |
| 25. |
27. |
| 29. |
31. |
| 33. |
35. |
| 37. |
39. |
| 41. |
43. |
| 45. |
47. |
| 49. |
51. |
| 51. |
55. |
| 57. |
59. |
| 61. |
63. |
| 65. |
67. |
| 69. |
71. a) 187 b) 46 c) 2 |
| 73. a) −104 b) 4 c) 40 | 75. 11 |
| 77. $10,800 | 77. $10,800 |
| 81. $58 | 83. 149 |
| 85. Answers will vary. | 87. Answers will vary. |
Attributions
This chapter has been adapted from “Add and Subtract Polynomials” in Prealgebra (OpenStax) by Lynn Marecek, MaryAnne Anthony-Smith, and Andrea Honeycutt Mathis, which is under a CC BY 4.0 Licence. Adapted by Izabela Mazur. See the Copyright page for more information.

