CHAPTER 8 Polynomials
8.6 Divide Polynomials
Learning Objectives
By the end of this section, you will be able to:
- Divide a polynomial by a monomial
Divide a Polynomial by a Monomial
In the last chapter, you learned how to divide a monomial by a monomial. As you continue to build up your knowledge of polynomials the next procedure is to divide a polynomial of two or more terms by a monomial.
The method we’ll use to divide a polynomial by a monomial is based on the properties of fraction addition. So we’ll start with an example to review fraction addition.
| The sum, | |
| simplifies to |
Now we will do this in reverse to split a single fraction into separate fractions.
We’ll state the fraction addition property here just as you learned it and in reverse.
Fraction Addition
If ![]() , and
, and ![]() are numbers where
are numbers where ![]() , then
, then
We use the form on the left to add fractions and we use the form on the right to divide a polynomial by a monomial.
| For example, | |
| can be written |
We use this form of fraction addition to divide polynomials by monomials.
Division of a Polynomial by a Monomial
To divide a polynomial by a monomial, divide each term of the polynomial by the monomial.
EXAMPLE 1
Find the quotient: ![]() .
.
| Divide each term of the numerator by the denominator. | |
| Simplify each fraction. |
TRY IT 1.1
Find the quotient: ![]() .
.
Show answer
![]()
TRY IT 1.2
Find the quotient: ![]() .
.
Show answer
![]()
Remember that division can be represented as a fraction. When you are asked to divide a polynomial by a monomial and it is not already in fraction form, write a fraction with the polynomial in the numerator and the monomial in the denominator.
EXAMPLE 2
Find the quotient: ![]() .
.
| Rewrite as a fraction. | |
| Divide each term of the numerator by the denominator. | |
| Simplify. |
TRY IT 2.1
Find the quotient: ![]() .
.
Show answer
![]()
TRY IT 2.2
Find the quotient: ![]() .
.
Show answer
![]()
When we divide by a negative, we must be extra careful with the signs.
EXAMPLE 3
Find the quotient: ![]() .
.
| Divide each term of the numerator by the denominator. | |
| Simplify. Remember, subtracting a negative is like adding a positive! |
TRY IT 3.1
Find the quotient: ![]() .
.
Show answer
![]()
TRY IT 3.2
Find the quotient: ![]() .
.
Show answer
![]()
EXAMPLE 4
Find the quotient: ![]() .
.
| Separate the terms. | |
| Simplify. |
TRY IT 4.1
Find the quotient: ![]() .
.
Show answer
![]()
TRY IT 4.2
Find the quotient: ![]() .
.
Show answer
![]()
EXAMPLE 5
Find the quotient: ![]() .
.
| Rewrite as a fraction. | |
| Separate the terms. | |
| Simplify. |
TRY IT 5.1
Find the quotient: ![]() .
.
Show answer
![]()
TRY IT 5.2
Find the quotient: ![]() .
.
Show answer
![]()
EXAMPLE 6
Find the quotient: ![]() .
.
| Separate the terms. | |
| Simplify. |
TRY IT 6.1
Find the quotient: ![]() .
.
Show answer
![]()
TRY IT 6.2
Find the quotient: ![]() .
.
Show answer
![]()
EXAMPLE 7
Find the quotient: ![]() .
.
| Separate the terms. | |
| Simplify. |
TRY IT 7.1
Find the quotient: ![]() .
.
Show answer
![]()
TRY IT 7.2
Find the quotient: ![]() .
.
Show answer
![]()
Access these online resources for additional instruction and practice with dividing polynomials:
Key Concepts
- Fraction Addition
- If
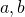 , and
, and  are numbers where
are numbers where 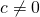 , then
, then
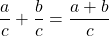 and
and 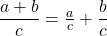
- If
- Division of a Polynomial by a Monomial
- To divide a polynomial by a monomial, divide each term of the polynomial by the monomial.
Practice Makes Perfect
Dividing Polynomial by Monomial
In the following exercises, divide each polynomial by the monomial.
| 1. |
2. |
| 3. |
4. |
| 5. |
6. |
| 7. |
8. |
| 9. |
10. |
| 11. |
12. |
| 13. |
14. |
| 15. |
16. |
| 17. |
18. |
| 19. |
20. |
| 21. |
22. |
| 23. |
24. |
| 25. |
26. |
| 27. |
28. |
| 29. |
30. |
| 31. |
32. |
Everyday Math
| 33. Handshakes At a company meeting, every employee shakes hands with every other employee. The number of handshakes is given by the expression |
34. Average cost Pictures Plus produces digital albums. The company’s average cost (in dollars) to make
|
Writing Exercises
| 35. Divide |
36. James divides |
Answers
| 1. |
3. |
5. |
| 7. |
9. |
11. |
| 13. |
15. |
17. |
| 19. |
21. |
23. |
| 25. |
27. |
29. |
| 31. |
33. 45 | 35. Answers will vary. |
Attributions
This chapter has been adapted from “Divide Polynomials” in Elementary Algebra (OpenStax) by Lynn Marecek and MaryAnne Anthony-Smith, which is under a CC BY 4.0 Licence. Adapted by Izabela Mazur. See the Copyright page for more information.

