9.3 Chapter Review

Izabela Mazur

CHAPTER 9 Trigonometry

9.3 Chapter Review

Review Exercises

Use Properties of Angles

In the following exercises, solve using properties of angles.

1. What is the supplement of a $\text{48}$ ° angle?	2. What is the complement of a $\text{61}$ ° angle?
3. Two angles are complementary. The smaller angle is $\text{24}$ ° less than the larger angle. Find the measures of both angles.	4. Two angles are supplementary. The larger angle is $\text{45}$ ° more than the smaller angle. Find the measures of both angles.

Use Properties of Triangles

In the following exercises, solve using properties of triangles.

5. The measures of two angles of a triangle are $22$ and $85$ degrees. Find the measure of the third angle.	6. One angle of a right triangle measures $41.5$ degrees. What is the measure of the other small angle?
7. One angle of a triangle is $\text{30}$ ° more than the smallest angle. The largest angle is the sum of the other angles. Find the measures of all three angles.	8. One angle of a triangle is twice the measure of the smallest angle. The third angle is $\text{60}$ ° more than the measure of the smallest angle. Find the measures of all three angles.

In the following exercises, $\Delta ABC$ is similar to $\Delta XYZ$ . Find the length of the indicated side.

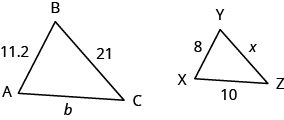
Two triangles are shown. Triangle ABC is on the left. The side across from A is labeled 21, across from B is b, and across from C is 11.2. Triangle XYZ is on the right. The side across from X is labeled x, across from Y is 10, and across from Z is 8.

9. side $x$

10. side $b$

Use the Pythagorean Theorem

In the following exercises, use the Pythagorean Theorem to find the length of the missing side. Round to the nearest tenth, if necessary.

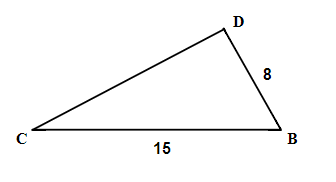
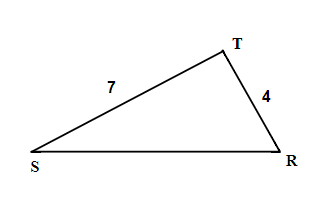
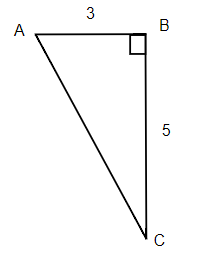
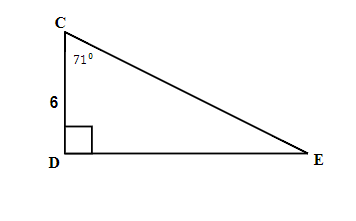
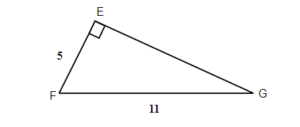
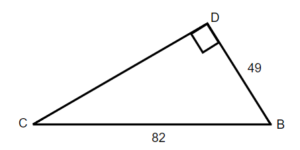
11.	12.
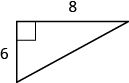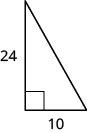
13.	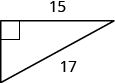14.
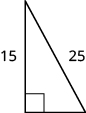15.	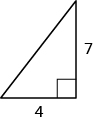16.

In the following exercises, solve. Approximate to the nearest tenth, if necessary.

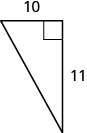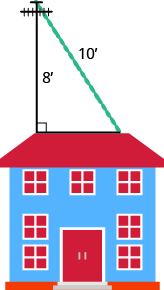
17. Sergio needs to attach a wire to hold the antenna to the roof of his house, as shown in the figure. The antenna is $8$ feet tall and Sergio has $10$ feet of wire. How far from the base of the antenna can he attach the wire?

An image of a house is shown. A 10-foot wire is going from the roof of the house to the ground. The wire hits the house at a height of 8 feet.

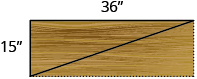
18. Seong is building shelving in his garage. The shelves are $36$ inches wide and $15$ inches tall. He wants to put a diagonal brace across the back to stabilize the shelves, as shown. How long should the brace be?

A rectangular shelf is shown, with a diagonal drawn in from the lower left corner to the upper right corner. The side is labeled 15 inches, the top is labeled 36 inches.

Find missing side of a right triangle using sine, cosine, or tangent ratios.

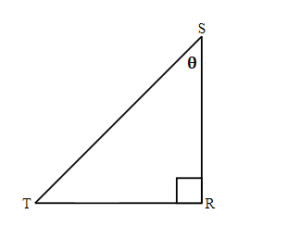
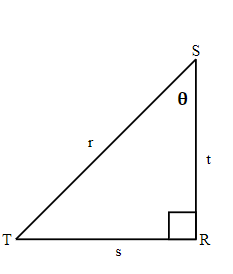
19. Label the triangle and find the sine cosine and tangent of θ.

20. If reference angle in above triangle is angle T, label the triangle and find the sine, cosine, and tangent of T.

Find missing angle of a right triangle using sine, cosine, or tangent ratios.

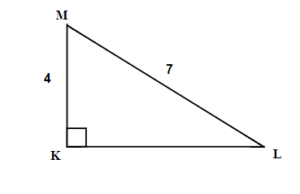
21. Find angle M

22. Find angle L.

Solve the right triangle.

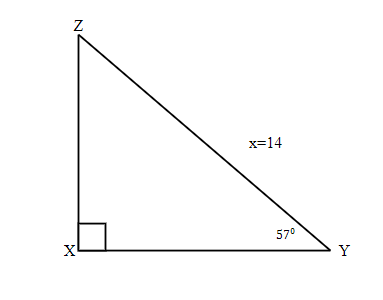
23. Solve the triangle.

24.

Solve applications using right angle trigonometry.

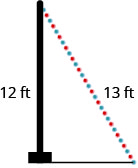
25. A 13-foot string of lights will be attached to the top of a 12-foot pole for a holiday display, as shown below. What is the angle that the string of lights makes with the ground?

A right triangle with one leg marked 12 and hypotenuse marked 13.

26. Brian borrowed a 20 foot extension ladder to use when he paints his house. If he sets the base of the ladder 6 feet from the house, as shown below, what is the angle that the ladder makes with the ground?

A house is shown with a ladder leaning against it. The ladder is marked 20’, and the distance from the house to the base of the ladder is marked 6’.

27. John puts the base of a 13-foot ladder five feet from the wall of his house as shown below. What is the angle between the top of the ladder and the house ?

A house is shown with a ladder leaning against it. The ladder is marked 13’, and the distance from the house to the base of the ladder is marked 5’.

28. The sun is at an angle of elevation of 35°. If Bob casts a shadow that is 6 ft long, how tall is Bob?

29. A 27 foot guy wire to a pole makes an angle of 63.7° with the ground. How high from the ground is the wire attached to the pole?

30. A lighthouse is 20 metres tall. If the observer is looking at a boat that is 30 metres away from the base of the lighthouse, what is the angle of depression?

Review Answers

1. 132°	3. 33°, 57°	5. 73°
7. 30°, 60°, 90°	9. 15	11. 26
13. 8	15. 8.1	17. 6 feet
19. sin θ = $\frac{s}{r}$ , cos θ = $\frac{t}{r}$ , tan θ = $\frac{s}{t}$	21. 55.2°	23. $\angle X$ = 90° , $\angle Y$ = 57° , $\angle Z$ = 33°x = 14, y = 11.7, z= 7.6
25. 67.4°	27. 22.6°	29. 24

Practice Test

1. What is the supplement of a $\angle 57$ ° angle?	2. Two angles are complementary. The smaller angle is $\text{16}$ ° less than the larger angle. Find the measures of both angles.
3. The measures of two angles of a triangle are $29$ and $75$ degrees. Find the measure of the third angle.	4. $\Delta BCD$ is similar to $\Delta SRT$ . Find the missing sides.
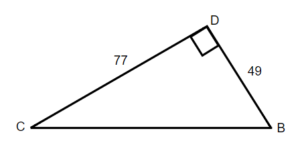
5. Use the Pythagorean Theorem to find the length of the missing side. Round to the nearest tenth, if necessary.	6. Find the hypotenuse.
7. Find angle G.	8. Solve the triangle.
9. The sun is at an angle 28°. If Adam casts a shadow that is 7 ft long, how tall is Adam?	10. The road rises 6 metres per every 100 horizontal metres. What is the angle of elevation.

Answers

1. 123°	2. 53°, 37°	3. 76°
4. b = 14, t = 7.5	5. b = 15.3	6. d = 18.4
7. $\angle G$ = 27°	8. $\angle C$ = 36.7°, $\angle B$ = 53.3°, $\angle D$ = 90°, c = 49, b = 65.7, d= 82	9. 5.5 ft
10. 3.4°