Chapter 3 Intrusive Igneous Rocks
3.2 Magma and Magma Formation
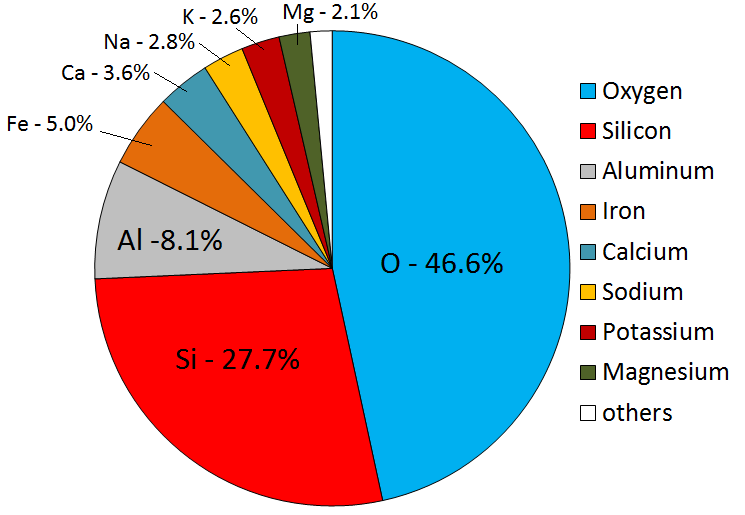
Magmas can vary widely in composition, but in general they are made up of only eight elements; in order of importance: oxygen, silicon, aluminum, iron, calcium, sodium, magnesium, and potassium (Figure 3.2.1). Oxygen, the most abundant element in magma, comprises a little less than half the total, followed by silicon at just over one-quarter. The remaining elements make up the other one-quarter. Magmas derived from crustal material are dominated by oxygen, silicon, aluminum, sodium, and potassium.
The composition of magma depends on the rock it was formed from (by melting), and the conditions of that melting. Magmas derived from the mantle have higher levels of iron, magnesium, and calcium, but they are still likely to be dominated by oxygen and silicon. All magmas have varying proportions of elements such as hydrogen, carbon, and sulphur, which are converted into gases like water vapour, carbon dioxide, and hydrogen sulphide as the magma cools.
Virtually all of the igneous rocks that we see on Earth are derived from magmas that formed from of existing rock, either in the upper mantle or the crust. Partial melting is what happens when only some parts of a rock melt; it takes place because rocks are not pure materials. Most rocks are made up of several minerals, each of which has a different melting temperature. The wax in a candle is a pure material. If you put some wax into a warm oven (50°C will do as the melting temperature of most wax is about 40°C) and leave it there for a while, it will soon start to melt. That’s complete melting, not partial melting. If instead you took a mixture of wax, plastic, aluminum, and glass and put it into the same warm oven, the wax would soon start to melt, but the plastic, aluminum, and glass would not melt (Figure 3.2.2a). That’s partial melting and the result would be solid plastic, aluminum, and glass surrounded by liquid wax (Figure 3.2.2b). If we heat the oven up to around 120°C, the plastic would melt too and mix with the liquid wax, but the aluminum and glass would remain solid (Figure 3.2.2c). Again this is partial melting. If we separated the wax/plastic “magma” from the other components and let it cool, it would eventually harden. As you can see from Figure 3.2.2d, the liquid wax and plastic have mixed, and on cooling, have formed what looks like a single solid substance. It is most likely that this is a very fine-grained mixture of solid wax and solid plastic, but it could also be some other substance that has formed from the combination of the two.
In this example, we partially melted some pretend rock to create some pretend magma. We then separated the magma from the source and allowed it to cool to make a new pretend rock with a composition quite different from the original material (it lacks glass and aluminum).
Of course partial melting in the real world isn’t exactly the same as in our pretend-rock example. The main differences are that rocks are much more complex than the four-component system we used, and the mineral components of most rocks have more similar melting temperatures, so two or more minerals are likely to melt at the same time to varying degrees. Another important difference is that when rocks melt, the process takes thousands to millions of years, not the 90 minutes it took in the pretend-rock example.
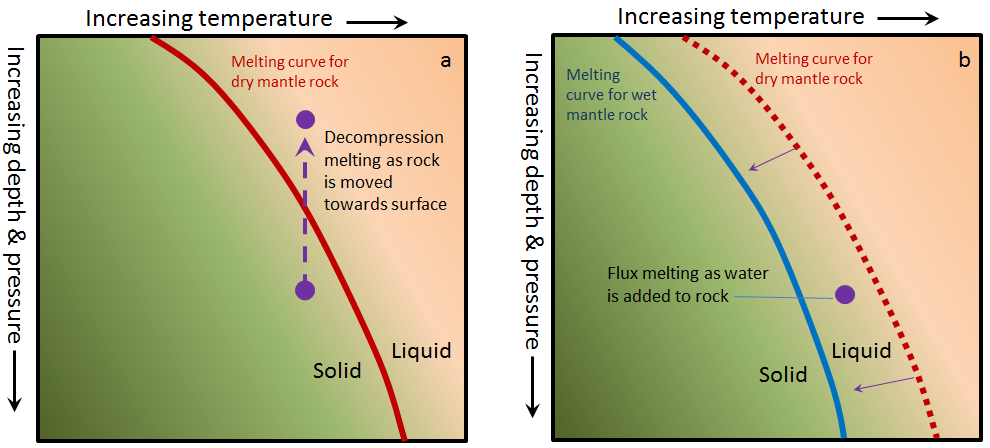
Contrary to what one might expect, and contrary to what we did to make our pretend rock, most partial melting of real rock does not involve heating the rock up. The two main mechanisms through which rocks melt are and . Decompression melting takes place within Earth when a body of rock is held at approximately the same temperature but the pressure is reduced. This happens because the rock is being moved toward the surface, either at a (a.k.a., hot spot), or in the upwelling part of a mantle convection cell.[1] The mechanism of decompression melting is shown in Figure 3.2.3a. If a rock that is hot enough to be close to its melting point is moved toward the surface, the pressure is reduced, and the rock can pass to the liquid side of its melting curve. At this point, partial melting starts to take place. The process of flux melting is shown in Figure 3.2.3b. If a rock is close to its melting point and some water (a flux that promotes melting) is added to the rock, the melting temperature is reduced (solid line versus dotted line), and partial melting starts.
The partial melting of rock happens in a wide range of situations, most of which are related to plate tectonics. The more important of these are shown in Figure 3.2.3. At both mantle plumes and in the upward parts of convection systems, rock is being moved toward the surface, the pressure is dropping, and at some point, the rock crosses to the liquid side of its melting curve. At subduction zones, water from the wet, subducting oceanic crust is transferred into the overlying hot mantle. This provides the flux needed to lower the melting temperature. In both of these cases, only partial melting takes place—typically only about 10% of the rock melts—and it is always the most silica-rich components of the rock that melt, creating a magma that is more silica-rich than the rock from which it is derived. (By analogy, the melt from our pretend rock is richer in wax and plastic than the “rock” from which it was derived.) The magma produced, being less dense than the surrounding rock, moves up through the mantle, and eventually into the crust.
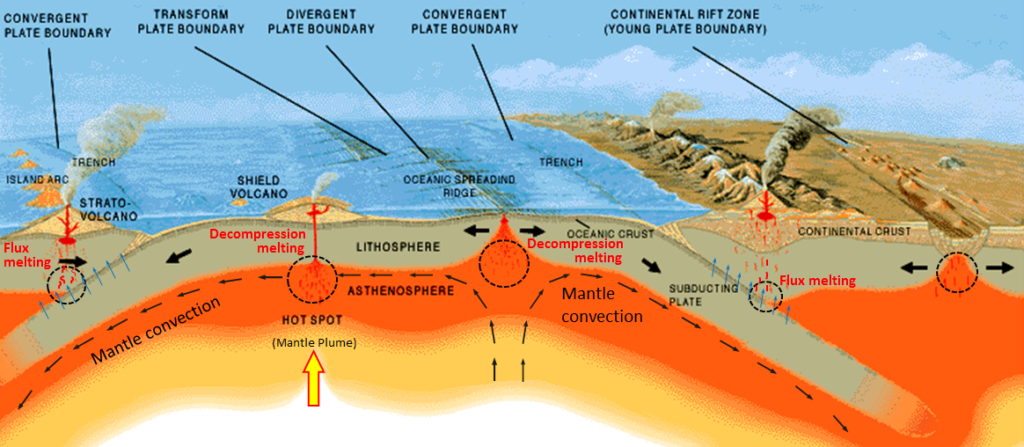
As it moves toward the surface, and especially when it moves from the mantle into the lower crust, the hot magma interacts with the surrounding rock. This typically leads to partial melting of the surrounding rock because most such magmas are hotter than the melting temperature of crustal rock. (In this case, melting is caused by an increase in temperature.) Again, the more silica-rich parts of the surrounding rock are preferentially melted, and this contributes to an increase in the silica content of the magma.
At very high temperatures (over 1300°C), most magma is entirely liquid because there is too much energy for the atoms to bond together. As the temperature drops, usually because the magma is slowly moving upward, things start to change. Silicon and oxygen combine to form silica tetrahedra, and then, as cooling continues, the tetrahedra start to link together to make chains (). These silica chains have the important effect of making the magma more viscous (less runny), and as we’ll see in Chapter 4, magma viscosity has significant implications for volcanic eruptions. As the magma continues to cool, crystals start to form.
Exercise 3.2 Making magma viscous
This is an experiment that you can do at home to help you understand the properties of magma. It will only take about 15 minutes, and all you need is half a cup of water and a few tablespoons of flour.
If you’ve ever made gravy, white sauce, or roux, you’ll know how this works.
Place about 1/2 cup (125 mL) of water in a saucepan over medium heat. Add 2 teaspoons (10 mL) of white flour (this represents silica) and stir while the mixture comes close to boiling. It should thicken like gravy because the gluten in the flour becomes polymerized into chains during this process.
Now you’re going to add more “silica” to see how this changes the viscosity of your magma. Take another 4 teaspoons (20 mL) of flour and mix it thoroughly with about 4 teaspoons (20 mL) of water in a cup and then add all of that mixture to the rest of the water and flour in the saucepan. Stir while bringing it back up to nearly boiling temperature, and then allow it to cool. This mixture should slowly become much thicker — something like porridge — because there is more gluten and more chains have been formed (see the photo).
This is analogous to magma, of course. As we’ll see below, magmas have quite variable contents of silica and therefore have widely varying viscosities (“thicknesses”) during cooling.
See Appendix 3 for Exercise 3.2 answers.
Image Descriptions
Figure 3.2.1 image description: The average elemental proportions in the Earth’s crust from the largest amount to the smallest amount. Oxygen (46.6%), Silicon (27.7%), Aluminum (8.1%), Iron (5.0%), Calcium (3.6%), Sodium (2.8%), Potassium (2.6%), Magnesium (2.1%), Others (1.5%). [Return to Figure 3.2.1]
Figure 3.2.3a image description: Dry mantle rock is predominately solid. However, its melting point is dependent on the temperature and pressure the rock is under. The higher the pressure (meaning the farther the rock is from the Earth’s surface), the more likely dry mantle rock is going to be solid. Dry mantle rock under extreme pressure requires a much higher temperature to melt than dry mantle rock under less pressure. As pressure drops (meaning as the rock rises towards the Earth’s surface), the required temperature to melt the mantle rock drops as well.
Figure 3.2.3b image description: In comparison to dry mantle rock, wet mantle rock under the same amount of pressure (at the same distance from the earth’s surface) requires a lower temperature to melt. When liquid is added to dry mantel rock at a pressure and temperature point in which wet mantle rock would be melted, flux melting occurs. [Return to Figure 3.2.3]
Media Attributions
- Figure 3.2.1, 3.2.2, 3.2.3, 3.2.5: © Steven Earle. CC BY.
- Figure 3.2.4: “Cross section” by José F. Vigil from This Dynamic Planet — a wall map produced jointly by the U.S. Geological Survey, the Smithsonian Institution, and the U.S. Naval Research Laboratory. Adapted by Steven Earle. Public domain.
- Mantle plumes are described in Chapter 4 and mantle convection in Chapter 9. ↵
the movement of sediment along a shoreline resulting from a longshore current and also from the swash and backwash on a beach face
a strong flow of water outward from a beach
Waves form on the ocean and on lakes because energy from the wind is transferred to the water. The stronger the wind, the longer it blows, and the larger the area of water over which it blows (the ), the larger the waves are likely to be.
The important parameters of a wave are the (the horizontal distance between two crests or two troughs), the (the vertical distance between a and a ), and the wave velocity (the speed at which wave crests move across the water) (Figure 17.1.1).
The typical sizes and speeds of waves in situations where they have had long enough to develop fully are summarized in Table 17.1. In a situation where the fetch is short (say 19 km on a lake) and the wind is only moderate (19 km/h), the waves will develop fully within 2 hours, but they will remain quite small (average amplitude about 27 cm, wavelength 8.5 m). On a large body of water (the ocean or a very large lake) with a fetch of 139 km and winds of 37 km/h, the waves will develop fully in 10 hours; the average amplitude will be around 1.5 m and average wavelength around 34 m. In the open ocean, with strong winds (92 km/h) that blow for at least 69 hours, the waves will average nearly 15 m high and their wavelengths will be over 200 m. Small waves (amplitudes under a metre) tend to have relatively shallow slopes (amplitude is 3% to 4% of wavelength), while larger waves (amplitudes over 10 m) have much steeper slopes (amplitude is 6% to 7% of wavelength). In other words, not only are large waves bigger than small ones, they are also generally more than twice as steep, and therefore many times more impressive—and potentially dangerous. It is important to recognize, however, that amplitudes decrease with distance from the area where the waves were generated. Waves on our coast that are generated by a storm near Japan will have similar wavelengths but lower amplitudes than those generated by a comparable storm just offshore.
| [Skip Table] | |||||||
| Wind Speed (kilometres per hour) | Fetch (kilometres) | Duration (hours) | Amplitude (metres) | Wavelength (metres) | Wave Period (seconds) | Wave Velocity (metres per second) | Wave Velocity (kilometres per hour) |
|---|---|---|---|---|---|---|---|
| 19 | 19 | 2 | 0.27 | 8.5 | 3.0 | 2.8 | 10.2 |
| 37 | 139 | 10 | 1.5 | 33.8 | 5.7 | 5.9 | 19.5 |
| 56 | 518 | 23 | 4.1 | 76.5 | 8.6 | 8.9 | 32.0 |
| 74 | 1,313 | 42 | 8.5 | 136 | 11.4 | 11.9 | 42.9 |
| 92 | 2,627 | 69 | 14.8 | 212 | 14.3 | 14.8 | 53.4 |
Exercise 17.1 Wave height versus length
This table shows the typical amplitudes and wavelengths of waves generated under different wind conditions. The steepness of a wave can be determined from these numbers and is related to the ratio: amplitude/wavelength.
- Calculate these ratios for the waves shown. The first one is done for you.
- How would these ratios change with increasing distance from the wind that produced the waves?
| Amplitude (metres) | Wavelength (metres) | Ratio (amplitude divided by wavelength) |
|---|---|---|
| 0.27 | 8.5 | 0.03 |
| 1.5 | 33.8 | |
| 4.1 | 76.5 | |
| 8.5 | 136 | |
| 14.8 | 212 |
See Appendix 3 for Exercise 17.1 answers.
Relatively small waves move at up to about 10 km/h and arrive on a shore about once every 3 seconds. Very large waves move about five times faster (over 50 km/h), but because their wavelengths are so much longer, they arrive less frequently—about once every 14 seconds.
As a wave moves across the surface of the water, the water itself mostly just moves up and down and only moves a small amount in the direction of wave motion. As this happens, a point on the water surface describes a circle with a diameter that is equal to the wave amplitude (Figure 17.1.2). This motion is also transmitted to the water underneath, and the water is disturbed by a wave to a depth of approximately one-half of the wavelength. Wave motion is illustrated quite clearly on the Wikipedia “Wind wave” site. If you look carefully at that animation, and focus on the small white dots in the water, you should be able to see how the amount that they move decreases with depth.
The one-half wavelength depth of disturbance of the water beneath a wave is known as the . Since ocean waves rarely have wavelengths greater than 200 m, and the open ocean is several thousand metres deep, the wave base does not normally interact with the bottom of the ocean. However, as waves approach the much shallower water near the shore, they start to “feel” the bottom, and they are affected by that interaction (Figure 17.1.3). The wave “orbits” are both flattened and slowed by dragging, and the implications are that the wave amplitude (height) increases and the wavelength decreases (the waves become much steeper). The ultimate result of this is that the waves lean forward, and eventually break (Figure 17.1.4).
Waves normally approach the shore at an angle, and this means that one part of the wave feels the bottom sooner than the rest of it, so the part that feels the bottom first slows down first. This process is illustrated in Figure 17.1.5, which is based on an aerial photograph showing actual waves approaching Long Beach on Vancouver Island. When the photo was taken, the waves (with crests shown as white lines in the diagram) were approaching at an angle of about 20° to the beach. The waves first reached shore at the southern end ("a" on the image). As they moved into shallow water they were slowed, and since the parts of the waves still in deep water ("b" on the image) were not slowed they were able catch up, and thus the waves became more parallel to the beach.
In open water, these waves had wavelengths close to 100 m. In the shallow water closer to shore, the wavelengths decreased to around 50 m, and in some cases, even less.
Even though they bend and become nearly parallel to shore, most waves still reach the shore at a small angle, and as each one arrives, it pushes water along the shore, creating what is known as a within the (the areas where waves are breaking) (Figure 17.1.6).
Exercise 17.2 Wave refraction
A series of waves (dashed lines) is approaching the coast on the map shown here.
The location of the depth contour that is equivalent to 1/2 of the wavelength is shown as a red dashed line.
Draw in the next several waves, showing how their patterns will change as they approach shallow water and the shore.
Show, with arrows, the direction of the resulting longshore current.
See Appendix 3 for Exercise 17.2 answers.
Another important effect of waves reaching the shore at an angle is that when they wash up onto the beach, they do so at an angle, but when that same wave water flows back down the beach, it moves straight down the slope of the beach (Figure 17.1.8). The upward-moving water, known as the , pushes sediment particles along the beach, while the downward-moving water, the , brings them straight back. With every wave that washes up and then down the beach, particles of sediment are moved along the beach in a zigzag pattern.
The combined effects of sediment transport within the surf zone by the longshore current and sediment movement along the beach by swash and backwash is known as . Longshore drift moves a tremendous amount of sediment along coasts (both oceans and large lakes) around the world, and it is responsible for creating a variety of depositional features that we’ll discuss in section 17.3.
A is another type of current that develops in the nearshore area, and has the effect of returning water that has been pushed up to the shore by incoming waves. As shown in Figure 17.1.9, rip currents flow straight out from the shore and are fed by the longshore currents. They die out quickly just outside the surf zone, but can be dangerous to swimmers who get caught in them. If part of a beach does not have a strong unidirectional longshore current, the rip currents may be fed by longshore currents going in both directions.
Rip currents are visible in Figure 17.1.10, a beach at Tunquen in Chile near Valparaiso. As is evident from the photo, the rips correspond with embayments in the beach profile. Three of them are indicated with arrows, but it appears that there may be several others farther along the beach.
Tides are related to very long-wavelength but low-amplitude waves on the ocean surface (and to a much lesser extent on very large lakes) that are caused by variations in the gravitational effects of the Sun and Moon. Tide amplitudes in shoreline areas vary quite dramatically from place to place. On the west coast of Canada, the tidal range is relatively high, in some areas as much as 6 m, while on most of the east coast the range is lower, typically around 2 m. A major exception is the Bay of Fundy between Nova Scotia and New Brunswick, where the daily range can be as great as 16 m. Anomalous tides like that are related to the shape and size of bays and inlets, which can significantly enhance the amplitude of the tidal surge. The Bay of Fundy has a natural oscillation cycle of 12.5 hours, and that matches the frequency of the rise and fall of the tides in the adjacent Atlantic Ocean. Ungava Bay, on Quebec’s north coast, has a similarly high tidal range.
As the tides rise and fall they push and pull a large volume of water in and out of bays and inlets and around islands. They do not have as significant an impact on coastal erosion and deposition as wind waves do, but they have an important influence on the formation of features within the intertidal zone, as we’ll see in the following sections.
Media Attributions
- Figures 17.1.1, 17.1.2, 17.1.3, 17.1.6, 17.1.7, 17.1.8, 17.1.9: © Steven Earle. CC BY.
- Figure 17.1.10: "Tunquen Chile" by Cecilia and Randy Lascody. Public domain.
a point extending out to sea
the tendency for an irregular coast to be straightened over time by coastal erosion processes
