6. Health Option
6.2 Ratio, Rate, and Percent; Health Applications
Learning Objectives
By the end of this section it is expected that you will be able to:
- Write a ratio as a fraction
- Application of ratio
- Write ratio as a fraction
- Find unit rate
- Use the definition of percent
- Convert percents to fractions and decimals
- Convert decimals and fractions to percents
Write a Ratio as a Fraction
Ratios
A ratio compares two numbers or two quantities that are measured with the same unit. The ratio of ![]() to
to ![]() is written
is written ![]()
In this section, we will use the fraction notation. When a ratio is written in fraction form, the fraction should be simplified. If it is an improper fraction, we do not change it to a mixed number. Because a ratio compares two quantities, we would leave a ratio as ![]() instead of simplifying it to
instead of simplifying it to ![]() so that we can see the two parts of the ratio.
so that we can see the two parts of the ratio.
EXAMPLE 1
Write each ratio as a fraction: a) ![]() b)
b) ![]() .
.
| Write as a fraction with the first number in the numerator and the second in the denominator. | |
| Simplify the fraction. |
We leave the ratio in b) as an improper fraction.
| Write as a fraction with the first number in the numerator and the second in the denominator. | |
| Simplify. |
TRY IT 1
Write each ratio as a fraction: a) ![]() b)
b) ![]() .
.
Show answer
Applications of Ratios
One real-world application of ratios that affects many people involves measuring cholesterol in blood. The ratio of total cholesterol to HDL cholesterol is one way doctors assess a person’s overall health. A ratio of less than ![]() to 1 is considered good.
to 1 is considered good.
EXAMPLE 2
Hector’s total cholesterol is ![]() mg/dl and his HDL cholesterol is
mg/dl and his HDL cholesterol is ![]() mg/dl. a) Find the ratio of his total cholesterol to his HDL cholesterol. b) Assuming that a ratio less than
mg/dl. a) Find the ratio of his total cholesterol to his HDL cholesterol. b) Assuming that a ratio less than ![]() to
to ![]() is considered good, what would you suggest to Hector?
is considered good, what would you suggest to Hector?
a) First, write the words that express the ratio. We want to know the ratio of Hector’s total cholesterol to his HDL cholesterol.
| Write as a fraction. | |
| Substitute the values. | |
| Simplify. |
b) Is Hector’s cholesterol ratio ok? If we divide ![]() by
by ![]() we obtain approximately
we obtain approximately ![]() , so
, so ![]() . Hector’s cholesterol ratio is high! Hector should either lower his total cholesterol or raise his HDL cholesterol.
. Hector’s cholesterol ratio is high! Hector should either lower his total cholesterol or raise his HDL cholesterol.
TRY IT 2
Find the patient’s ratio of total cholesterol to HDL cholesterol using the given information.
Total cholesterol is ![]() mg/dL and HDL cholesterol is
mg/dL and HDL cholesterol is ![]() mg/dL.
mg/dL.
Show answer
![]()
Write a Rate as a Fraction
Frequently, using rate, we compare two different types of measurements. Examples of rates are ![]() kilometres in
kilometres in ![]() hours,
hours, ![]() words in
words in ![]() minutes, and
minutes, and ![]() dollars per
dollars per ![]() ounces.
ounces.
Rate
A rate compares two quantities of different units. A rate is usually written as a fraction.
When writing a fraction as a rate, we put the first given amount with its units in the numerator and the second amount with its units in the denominator. When rates are simplified, the units remain in the numerator and denominator.
EXAMPLE 3
A healthy heart has a rate around 72 beats per 60 seconds. Write this rate as a fraction.
| Write as a fraction, 72 beats in the numerator and 60 seconds in the denominator. | |
So ![]() beats in
beats in ![]() seconds is equivalent to
seconds is equivalent to ![]() .
.
TRY IT 3
Write the rate as a fraction: ![]() heartbeats in
heartbeats in ![]() seconds.
seconds.
Show answer
![]()
Find Unit Rate
In the last example, we calculated that a healthy heart beats at a rate of ![]() . This tells us that every 5 seconds there are 6 heart beats. This is correct, but not very useful. We usually want the rate to reflect the number of beats in one second. A rate that has a denominator of
. This tells us that every 5 seconds there are 6 heart beats. This is correct, but not very useful. We usually want the rate to reflect the number of beats in one second. A rate that has a denominator of ![]() unit is referred to as a unit rate.
unit is referred to as a unit rate.
Unit Rate
A unit rate is a rate with denominator of ![]() unit.
unit.
To convert a rate to a unit rate, we divide the numerator by the denominator. This gives us a denominator of ![]() .
.
EXAMPLE 4
Marta had ![]() heartbeats in
heartbeats in![]() . What is Marta’s heartbeat rate?
. What is Marta’s heartbeat rate?
| Start with a rate of heartbeats to minutes. Then divide. | |
| Write as a rate. | |
| Divide the numerator by the denominator. | |
| Rewrite as a rate. |
Marta’s heartbeat rate is ![]() per minute.
per minute.
TRY IT 4
Find the unit rate: ![]() in
in ![]() minutes.
minutes.
Show answer
\68 heartbeats/minute
Use the Definition of Percent
How many cents are in one dollar? There are ![]() cents in a dollar. How many years are in a century? There are
cents in a dollar. How many years are in a century? There are ![]() years in a century. Does this give you a clue about what the word “percent” means? It is really two words, “per cent,” and means per one hundred. A percent is a ratio whose denominator is
years in a century. Does this give you a clue about what the word “percent” means? It is really two words, “per cent,” and means per one hundred. A percent is a ratio whose denominator is ![]() . We use the percent symbol
. We use the percent symbol ![]() to show percent.
to show percent.
Percent
A percent is a ratio whose denominator is ![]() .
.
According to the data from Statistics Canada (2009), ![]() of 6-11 year olds have or have had a cavity. This means
of 6-11 year olds have or have had a cavity. This means ![]() out of every
out of every ![]() of 6-11 year olds have or have had a cavity. As (Figure 1) shows out of the
of 6-11 year olds have or have had a cavity. As (Figure 1) shows out of the ![]() squares on the grid,
squares on the grid, ![]() are shaded, which we write as the ratio
are shaded, which we write as the ratio ![]() .
.

Similarly, ![]() means a ratio of
means a ratio of ![]() means a ratio of
means a ratio of ![]() and
and ![]() means a ratio of
means a ratio of ![]() . In words, “one hundred percent” means the total
. In words, “one hundred percent” means the total ![]() is
is ![]() , and since
, and since ![]() , we see that
, we see that ![]() means
means ![]() whole.
whole.
EXAMPLE 5
According to a Government of Canada report updated on \left(July 9, 2021\right \text{,}\phantom{\rule{0.2em}{0ex}}\text{68\%}\) of total population received at least on dose of COVID-19 vaccine. Write this percent as a ratio.
| The amount we want to convert is 68%. | |
| Write the percent as a ratio. Remember that percent means per 100. |
TRY IT 5
Write the percent as a ratio.
According to the report from example 5, ![]() of total population is partially vaccinated.
of total population is partially vaccinated.
Show answer
![]()
Convert Percents to Fractions and Decimals
Since percents are ratios, they can easily be expressed as fractions. Remember that percent means per ![]() , so the denominator of the fraction is
, so the denominator of the fraction is ![]() .
.
Convert a Percent to a Fraction.
- Write the percent as a ratio with the denominator
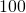 .
. - Simplify the fraction if possible.
EXAMPLE 6
According to the report from example 5, ![]() of total population is fully vaccinated.Convert the percent to a fraction:
of total population is fully vaccinated.Convert the percent to a fraction:
| Write as a ratio with denominator 100. | |
| Simplify. |
TRY IT 6
According to the report from example 5, just slightly over ![]() of 12 years and older population is fully vaccinated.Convert the percent to a fraction:
of 12 years and older population is fully vaccinated.Convert the percent to a fraction:
Show answer
![]()
To convert a percent to a decimal, we first convert it to a fraction and then change the fraction to a decimal.
HOW TO: Convert a Percent to a Decimal
- Write the percent as a ratio with the denominator
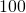 .
. - Convert the fraction to a decimal by dividing the numerator by the denominator.
EXAMPLE 7
a) Adult males typically are composed of about 60 % water. Convert the percent to a decimal.
b) Adult females typically are composted of 55% water. Convert the percent to a decimal
Because we want to change to a decimal, we will leave the fractions with denominator ![]() instead of removing common factors.
instead of removing common factors.
| a) | |
| Write as a ratio with denominator 100. | |
| Change the fraction to a decimal by dividing the numerator by the denominator. |
| b) | |
| Write as a ratio with denominator 100. | |
| Change the fraction to a decimal by dividing the numerator by the denominator. |
TRY IT 7
Convert each percent to a decimal:
Show answer
- 0.09
- 0.87
To convert a percent number to a decimal number, we move the decimal point two places to the left and remove the ![]() sign. (Sometimes the decimal point does not appear in the percent number, but just like we can think of the integer
sign. (Sometimes the decimal point does not appear in the percent number, but just like we can think of the integer ![]() as
as ![]() , we can think of
, we can think of ![]() as
as ![]() .) Notice that we may need to add zeros in front of the number when moving the decimal to the left.
.) Notice that we may need to add zeros in front of the number when moving the decimal to the left.
(Figure 2) uses the percents in the table above and shows visually how to convert them to decimals by moving the decimal point two places to the left.
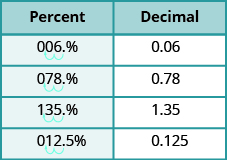
Convert Decimals and Fractions to Percents
To convert a decimal to a percent, remember that percent means per hundred. If we change the decimal to a fraction whose denominator is ![]() , it is easy to change that fraction to a percent.
, it is easy to change that fraction to a percent.
HOW TO: Convert a Decimal to a Percent
- Write the decimal as a fraction.
- If the denominator of the fraction is not
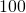 , rewrite it as an equivalent fraction with denominator
, rewrite it as an equivalent fraction with denominator 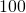 .
. - Write this ratio as a percent.
EXAMPLE 8
Convert each decimal to a percent: a) ![]() b)
b) ![]()
| a) | |
| Write as a fraction. The denominator is 100. | |
| Write this ratio as a percent. |
| b) | |
| The denominator is 100. | |
| Write this ratio as a percent. |
TRY IT 8
Convert each decimal to a percent: a)![]() b)
b)![]()
Show answer
- 4%
- 41%
To convert a decimal to a percent, we move the decimal point two places to the right and then add the percent sign.
(Figure.3) uses the decimal numbers in the table above and shows visually to convert them to percents by moving the decimal point two places to the right and then writing the ![]() sign.
sign.

Now we also know how to change decimals to percents. So to convert a fraction to a percent, we first change it to a decimal and then convert that decimal to a percent.
HOW TO: Convert a Fraction to a Percent
- Convert the fraction to a decimal.
- Convert the decimal to a percent.
EXAMPLE 9
Convert each fraction or mixed number to a percent: a) ![]() b)
b) ![]() c)
c) ![]()
To convert a fraction to a decimal, divide the numerator by the denominator.
| a) | |
| Change to a decimal. | |
| Write as a percent by moving the decimal two places. | 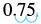 |
| b) | |
| Change to a decimal. | |
| Write as a percent by moving the decimal two places. | 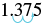 |
| c) | |
| Write as an improper fraction. | |
| Change to a decimal. | |
| Write as a percent. | 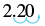 |
Notice that we needed to add zeros at the end of the number when moving the decimal two places to the right.
TRY IT 9
Convert each fraction or mixed number to a percent: a) ![]() b)
b) ![]() c)
c) ![]()
Show answer
- 62.5%
- 275%
- 340%
Sometimes when changing a fraction to a decimal, the division continues for many decimal places and we will round off the quotient. The number of decimal places we round to will depend on the situation. If the decimal involves money, we round to the hundredths place. For most other cases in this book we will round the number to the nearest thousandth, so the percent will be rounded to the nearest tenth.
EXAMPLE 10
Convert ![]() to a percent.
to a percent.
To change a fraction to a decimal, we divide the numerator by the denominator.
| Change to a decimal—rounding to the nearest thousandth. | |
| Write as a percent. |
TRY IT 10
Convert the fraction to a percent: ![]()
Show answer
42.9%
When we first looked at fractions and decimals, we saw that fractions converted to a repeating decimal. When we converted the fraction ![]() to a decimal, we wrote the answer as
to a decimal, we wrote the answer as ![]() . We will use this same notation, as well as fraction notation, when we convert fractions to percents in the next example.
. We will use this same notation, as well as fraction notation, when we convert fractions to percents in the next example.
EXAMPLE 11
Statistics Canada reported in 2018 that approximately ![]() of Canadian adults are obese. Convert the fraction
of Canadian adults are obese. Convert the fraction ![]() to a percent.
to a percent.
| Change to a decimal. | 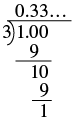 |
| Write as a repeating decimal. | |
| Write as a percent. |
We could also write the percent as ![]() .
.
TRY IT 11
Convert the fraction to a percent:
According to the Canadian Census 2016, about ![]() people within the population of Canada are between the ages of
people within the population of Canada are between the ages of ![]() and
and ![]() .
.
Show answer
![]()
Access to Additional Online Resources
Glossary
- ratio
- A ratio compares two numbers or two quantities that are measured with the same unit. The ratio of
 to
to 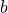 is written
is written  to
to 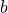 ,
, 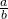 , or
, or 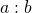 .
.
- rate
- A rate compares two quantities of different units. A rate is usually written as a fraction.
- unit rate
- A unit rate is a rate with denominator of 1 unit.
-
- percent
- A percent is a ratio whose denominator is
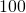 .
.
Key Concepts
- Convert a percent to a fraction.
- Write the percent as a ratio with the denominator 100.
- Simplify the fraction if possible.
- Convert a percent to a decimal.
- Write the percent as a ratio with the denominator 100.
- Convert the fraction to a decimal by dividing the numerator by the denominator.
- Convert a decimal to a percent.
- Write the decimal as a fraction.
- If the denominator of the fraction is not 100, rewrite it as an equivalent fraction with denominator 100.
- Write this ratio as a percent.
- Convert a fraction to a percent.
- Convert the fraction to a decimal.
- Convert the decimal to a percent.
6.2 Exercise Set
In the following exercises, write each ratio as a fraction.
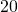 to
to 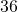
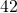 to
to 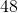
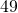 to
to 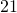
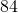 to
to 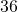
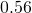 to
to 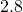
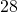 ounces to
ounces to 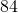 ounces
ounces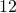 feet to
feet to 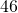 feet
feet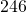 milligrams to
milligrams to 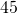 milligrams
milligrams- total cholesterol of
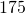 to HDL cholesterol of
to HDL cholesterol of 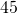
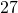 inches to
inches to 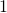 foot
foot
In the following exercises, find the unit rate. Round to two decimal places, if necessary.
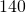 calories per
calories per 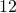 ounces
ounces- total cholesterol is
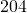 mg/dL and HDL cholesterol is
mg/dL and HDL cholesterol is 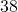 mg/dL
mg/dL - 584 beats in 8 minutes
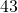 pounds in
pounds in 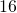 weeks
weeks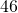 beats in
beats in 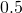 minute
minute
- A popular fast food burger weighs
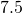 ounces and contains
ounces and contains 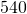 calories,
calories, 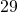 grams of fat,
grams of fat, 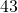 grams of carbohydrates, and
grams of carbohydrates, and 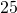 grams of protein. Find the unit rate of:
grams of protein. Find the unit rate of:
- calories per ounce
- grams of fat per ounce
- grams of carbohydrates per ounce
- grams of protein per ounce. Round to two decimal places.
In the following exercises, write each percent as a ratio.
- A patient health insurance covers
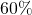 of the cost of his medication.
of the cost of his medication. 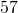 out of
out of 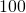 nursing candidates received their degree at a community college.
nursing candidates received their degree at a community college.
In the following exercises, convert each percent to a fraction and simplify all fractions.
In the following exercises, convert each percent to a decimal.
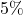
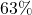
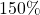
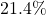
- COVID-19 vaccines, the Pfizer and Moderna have the hightest efficiency at around
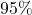
- A couple plans to have two children. The probability they will have two girls is
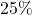 .
.
In the following exercises, convert each decimal to a percent.
In the following exercises, convert each fraction to a percent.
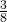
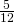
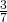
- According to the Government of Canada, in
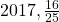 of Canadian adults were overweight or obese.
of Canadian adults were overweight or obese.
Answers
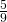
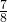
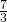
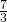
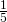
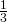
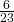
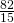
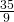
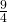
- 11.67 calories/ounce
- 2.73 lbs./sq. in.
- 73 beats/minute
- 2.69 lbs./week
- 92 beats/minute
-
- 72 calories/ounce
- 3.87 grams of fat/ounce
- 5.73 grams carbs/once
- 3.33 grams protein/ounce
-
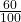
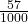

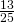
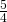
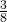
- 0.05
- 0.63
- 1.5
- 0.214
- 0.95
- 0.25
- 18%
- 135%
- 300%
- 0.9%
- 37.5%
- 41.7%
- 42.9%
Attributions
- This chapter has been adapted from “Understand Percent” in Prealgebra (OpenStax) by Lynn Marecek, MaryAnne Anthony-Smith, and Andrea Honeycutt Mathis, which is under a CC BY 4.0 Licence. Adapted by Izabela Mazur. See the Copyright page for more information.
- OER.hawaii.edu
- Wikipedia
- Government of Canada Statistics

