3. Equations and their Graphs
3.4 Understand Slope of a Line
Learning Objectives
By the end of this section it is expected that you will be able to:
- Use
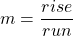 to find the slope of a line from its graph
to find the slope of a line from its graph - Find the slope of horizontal and vertical lines
- Use the slope formula to find the slope of a line between two points
- Graph a line given a point and the slope
- Solve slope applications
When you graph linear equations, you may notice that some lines tilt up as they go from left to right and some lines tilt down. Some lines are very steep and some lines are flatter. What determines whether a line tilts up or down or if it is steep or flat?
In mathematics, the ‘tilt’ of a line is called the slope of the line. The concept of slope has many applications in the real world. The pitch of a roof, grade of a highway, and a ramp for a wheelchair are some examples where you literally see slopes. And when you ride a bicycle, you feel the slope as you pump uphill or coast downhill.
In this section, we will explore the concept of slope.
The slope of a line is the ratio of the rise to the run. In mathematics, it is always referred to with the letter ![]() .
.
Slope of a line
The slope of a line of a line is ![]() .
.
The rise measures the vertical change and the run measures the horizontal change between two points on the line.
Positive and negative slopes
We ‘read’ a line from left to right just like we read words in English. As you read from left to right, the line is going up; it has positive slope. The line is going down; it has negative slope.

Use 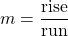 to Find the Slope of a Line from its Graph
to Find the Slope of a Line from its Graph
We’ll look at some graphs on the ![]() -coordinate plane and see how to find their slopes.
-coordinate plane and see how to find their slopes.
To find the slope, we must count out the rise and the run. But where do we start?
We locate two points on the line whose coordinates are integers. We then start with the point on the left and sketch a right triangle, so we can count the rise and run.
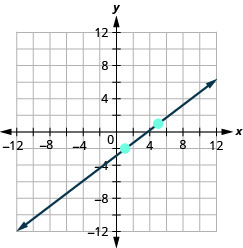
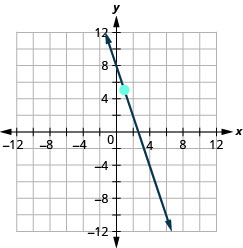
EXAMPLE 1
Find the slope of the line shown.

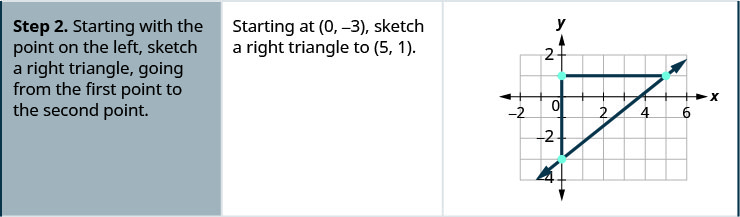


TRY IT 1
Find the slope of the line shown.
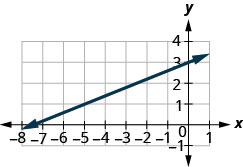
Show answer
![]()
HOW TO: Find the slope of a line from its graph using m = rise / run.
- Locate two points on the line whose coordinates are integers.
- Starting with the point on the left, sketch a right triangle, going from the first point to the second point.
- Count the rise and the run on the legs of the triangle.
- Take the ratio of rise to run to find the slope,
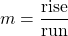 .
.
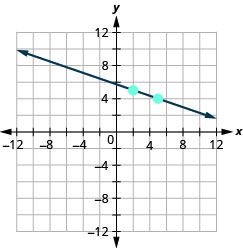
EXAMPLE 2
Find the slope of the line shown.
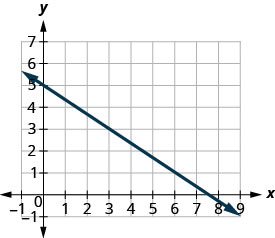
| Locate two points on the graph whose coordinates are integers. | |
| Which point is on the left? | |
| Starting at |
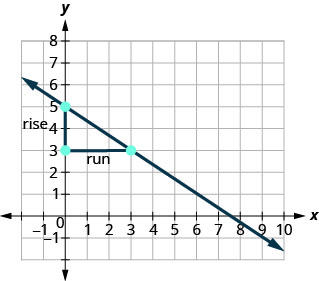 |
| Count the rise—it is negative. | The rise is |
| Count the run. | The run is 3. |
| Use the slope formula. | |
| Substitute the values of the rise and run. | |
| Simplify. | |
| The slope of the line is |
So ![]() increases by 3 units as
increases by 3 units as ![]() decreases by 2 units.
decreases by 2 units.
What if we used the points ![]() and
and ![]() to find the slope of the line?
to find the slope of the line?
The rise would be ![]() and the run would be 9. Then
and the run would be 9. Then ![]() , and that simplifies to
, and that simplifies to ![]() . Remember, it does not matter which points you use—the slope of the line is always the same.
. Remember, it does not matter which points you use—the slope of the line is always the same.
TRY IT 2
Find the slope of the line shown.
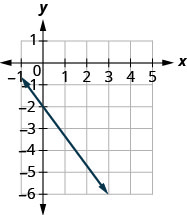
Show answer
![]()
In the last two examples, the lines had y-intercepts with integer values, so it was convenient to use the y-intercept as one of the points to find the slope. In the next example, the y-intercept is a fraction. Instead of using that point, we’ll look for two other points whose coordinates are integers. This will make the slope calculations easier.
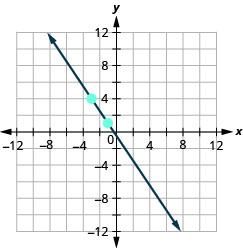
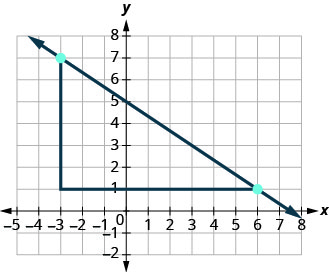
EXAMPLE 3
Find the slope of the line shown.
| Locate two points on the graph whose coordinates are integers. | |
| Which point is on the left? | |
| Starting at |
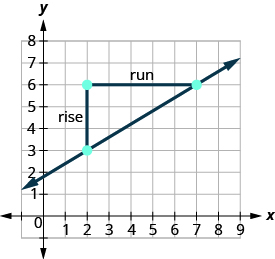 |
| Count the rise. | The rise is 3. |
| Count the run. | The run is 5. |
| Use the slope formula. | |
| Substitute the values of the rise and run. | |
| The slope of the line is |
This means that ![]() increases 5 units as
increases 5 units as ![]() increases 3 units.
increases 3 units.
When we used geoboards to introduce the concept of slope, we said that we would always start with the point on the left and count the rise and the run to get to the point on the right. That way the run was always positive and the rise determined whether the slope was positive or negative.
What would happen if we started with the point on the right?
Let’s use the points ![]() and
and ![]() again, but now we’ll start at
again, but now we’ll start at ![]() .
.
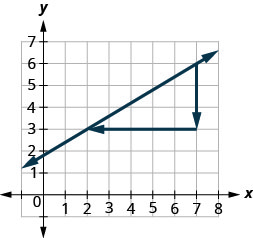
| Count the rise. | The rise is |
| Count the run. It goes from right to left, so it is negative. | The run is |
| Use the slope formula. | |
| Substitute the values of the rise and run. | |
| The slope of the line is |
It does not matter where you start—the slope of the line is always the same.
TRY IT 3
Find the slope of the line shown.
Show answer
![]()
Find the Slope of Horizontal and Vertical Lines
Do you remember what was special about horizontal and vertical lines? Their equations had just one variable.
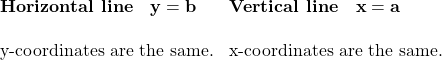
So how do we find the slope of the horizontal line ![]() ? One approach would be to graph the horizontal line, find two points on it, and count the rise and the run. Let’s see what happens when we do this.
? One approach would be to graph the horizontal line, find two points on it, and count the rise and the run. Let’s see what happens when we do this.
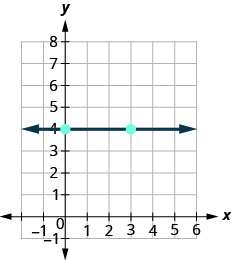
| What is the rise? | The rise is |
| Count the run. | The run is |
| What is the slope? | 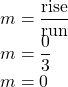 |
| The slope of the horizontal line |
All horizontal lines have slope 0. When the y-coordinates are the same, the rise is 0.
Slope of a horizontal line
The slope of a horizontal line, ![]() , is 0.
, is 0.
The floor of your room is horizontal. Its slope is 0. If you carefully placed a ball on the floor, it would not roll away.
Now, we’ll consider a vertical line, the line.
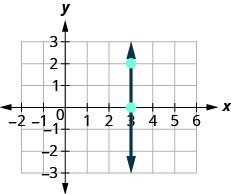
| What is the rise? | The rise is |
| Count the run. | The run is |
| What is the slope? | 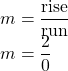 |
But we can’t divide by 0. Division by 0 is not defined. So we say that the slope of the vertical line ![]() is undefined.
is undefined.
The slope of any vertical line is undefined. When the x-coordinates of a line are all the same, the run is 0.
Slope of a vertical line
The slope of a vertical line, ![]() , is undefined.
, is undefined.
EXAMPLE 4
Find the slope of each line:
a) ![]() b)
b) ![]() .
.
a) ![]()
This is a vertical line.
Its slope is undefined.
b) ![]()
This is a horizontal line.
It has slope 0.
TRY IT 4
Find the slope of the line: ![]()
Show answer
undefined
Quick guide to the slopes of lines
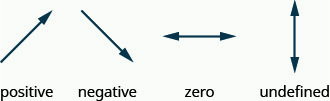
Remember, we ‘read’ a line from left to right, just like we read written words in English.
Use the Slope Formula to find the Slope of a Line Between Two Points
Sometimes we’ll need to find the slope of a line between two points when we don’t have a graph to count out the rise and the run. We could plot the points on grid paper, then count out the rise and the run, but as we’ll see, there is a way to find the slope without graphing. Before we get to it, we need to introduce some algebraic notation.
We have seen that an ordered pair ![]() gives the coordinates of a point. But when we work with slopes, we use two points. How can the same symbol
gives the coordinates of a point. But when we work with slopes, we use two points. How can the same symbol ![]() be used to represent two different points? Mathematicians use subscripts to distinguish the points.
be used to represent two different points? Mathematicians use subscripts to distinguish the points.
![]()
The use of subscripts in math is very much like the use of last name initials in elementary school. Maybe you remember Laura C. and Laura M. in your third grade class?
We will use ![]() to identify the first point and
to identify the first point and ![]() to identify the second point.
to identify the second point.
If we had more than two points, we could use ![]() ,
, ![]() , and so on.
, and so on.
Let’s see how the rise and run relate to the coordinates of the two points by taking another look at the slope of the line between the points ![]() and
and ![]() .
.
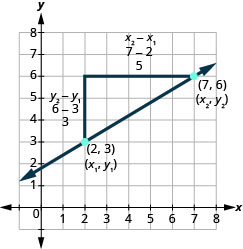
Since we have two points, we will use subscript notation, ![]()
![]() .
.
On the graph, we counted the rise of 3 and the run of 5.
Notice that the rise of 3 can be found by subtracting the y-coordinates 6 and 3.
![]()
And the run of 5 can be found by subtracting the x-coordinates 7 and 2.
![]()
We know ![]() . So
. So ![]() .
.
We rewrite the rise and run by putting in the coordinates ![]() .
.
But 6 is ![]() , the y-coordinate of the second point and 3 is
, the y-coordinate of the second point and 3 is ![]() , the y-coordinate of the first point.
, the y-coordinate of the first point.
So we can rewrite the slope using subscript notation. ![]()
Also, 7 is ![]() , the x-coordinate of the second point and 2 is
, the x-coordinate of the second point and 2 is ![]() , the x-coordinate of the first point.
, the x-coordinate of the first point.
So, again, we rewrite the slope using subscript notation. ![]()
We’ve shown that ![]() is really another version of
is really another version of ![]() . We can use this formula to find the slope of a line when we have two points on the line.
. We can use this formula to find the slope of a line when we have two points on the line.
Slope formula
The slope of the line between two points ![]() and
and ![]() is
is
![]()
This is the slope formula.
The slope is:

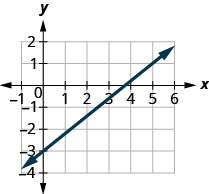
EXAMPLE 5
Use the slope formula to find the slope of the line between the points ![]() and
and ![]() .
.
| We’ll call |
|
| Use the slope formula. | |
| Substitute the values. | |
| Simplify the numerator and the denominator. | |
| Simplify. |
Let’s confirm this by counting out the slope on a graph using ![]() .
.
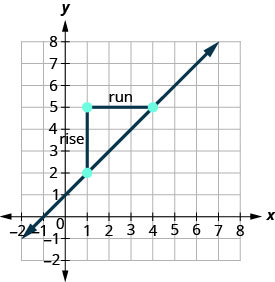
It doesn’t matter which point you call point #1 and which one you call point #2. The slope will be the same. Try the calculation yourself.
TRY IT 5
Use the slope formula to find the slope of the line through the points: ![]() and
and ![]() .
.
Show answer
1
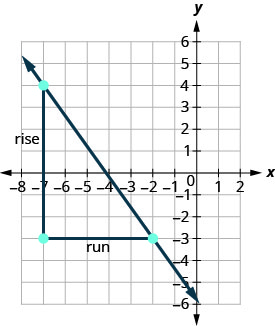
EXAMPLE 6
Use the slope formula to find the slope of the line through the points ![]() and
and ![]() .
.
| We’ll call |
|
| Use the slope formula. | |
| Substitute the values. | |
| Simplify. | 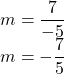 |
Let’s verify this slope on the graph shown.
TRY IT 6
Use the slope formula to find the slope of the line through the points: ![]() and
and ![]()
Show answer
![]()
Graph a Line Given a Point and the Slope
Up to now, in this chapter, we have graphed lines by plotting points, by using intercepts, and by recognizing horizontal and vertical lines.
One other method we can use to graph lines is called the point–slope method. We will use this method when we know one point and the slope of the line. We will start by plotting the point and then use the definition of slope to draw the graph of the line.
EXAMPLE 7
Graph the line passing through the point ![]() whose slope is
whose slope is ![]() .
.




EXAMPLE 7
Graph the line passing through the point ![]() with the slope
with the slope ![]() .
.
Show answer
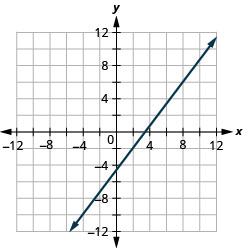
Graph a line given a point and the slope.
- Plot the given point.
- Use the slope formula
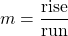 to identify the rise and the run.
to identify the rise and the run. - Starting at the given point, count out the rise and run to mark the second point.
- Connect the points with a line.
EXAMPLE 8
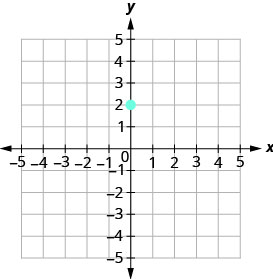
Graph the line with y-intercept 2 whose slope is ![]() .
.
Plot the given point, the y-intercept, ![]() .
.
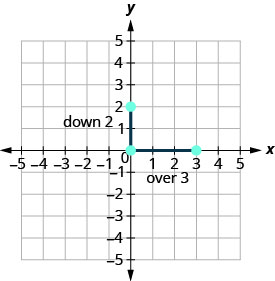
| Identify the rise and the run. | |
Count the rise and the run. Mark the second point.
Connect the two points with a line.
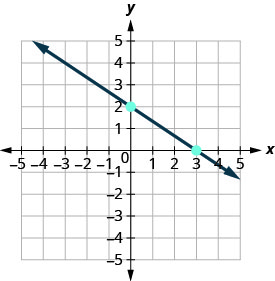
You can check your work by finding a third point. Since the slope is ![]() , it can be written as
, it can be written as ![]() . Go back to
. Go back to ![]() and count out the rise, 2, and the run,
and count out the rise, 2, and the run, ![]() .
.
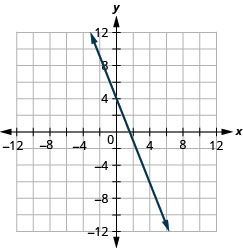
TRY IT 8
Graph the line with the y-intercept 4 and slope ![]()
Show answer
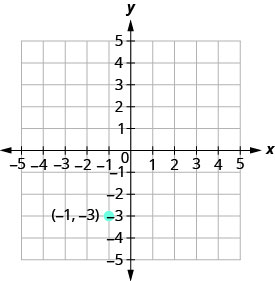
EXAMPLE 9
Graph the line passing through the point ![]() whose slope is
whose slope is ![]()
Plot the given point.
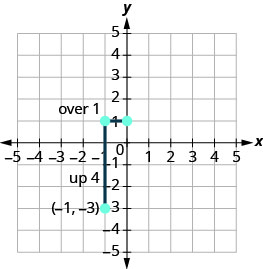
| Identify the rise and the run. | |
| Write 4 as a fraction. | |
Count the rise and run and mark the second point.
Connect the two points with a line.
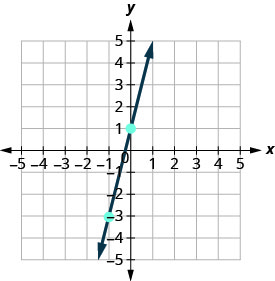
You can check your work by finding a third point. Since the slope is ![]() , it can be written as
, it can be written as ![]() . Go back to
. Go back to ![]() and count out the rise,
and count out the rise, ![]() , and the run,
, and the run, ![]() .
.
TRY IT 9
Graph the line with the point ![]() and slope
and slope ![]() .
.
Show answer
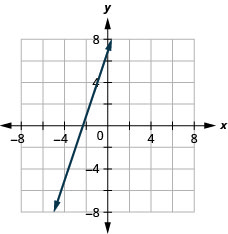
Solve Slope Applications
At the beginning of this section, we said there are many applications of slope in the real world. Let’s look at a few now.
EXAMPLE 10
The ‘pitch’ of a building’s roof is the slope of the roof. Knowing the pitch is important in climates where there is heavy snowfall. If the roof is too flat, the weight of the snow may cause it to collapse. What is the slope of the roof shown?
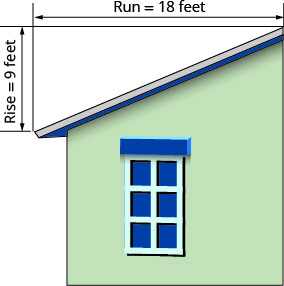
| Use the slope formula. | |
| Substitute the values for rise and run. | |
| Simplify. | |
| The slope of the roof is |
|
| The roof rises 1 foot for every 2 feet of horizontal run. |
TRY IT 10
Use (Example 10), substituting the rise = 14 and run = 24.
Show answer
![]()
EXAMPLE 11
Have you ever thought about the sewage pipes going from your house to the street? They must slope down ![]() inch per foot in order to drain properly. What is the required slope?
inch per foot in order to drain properly. What is the required slope?

| Use the slope formula. | 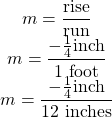 |
| Simplify. | |
| The slope of the pipe is |
The pipe drops 1 inch for every 48 inches of horizontal run.
TRY IT 11
Find the slope of a pipe that slopes down ![]() inch per foot.
inch per foot.
Show answer
![]()
Key Concepts
- Find the Slope of a Line from its Graph using
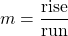
- Locate two points on the line whose coordinates are integers.
- Starting with the point on the left, sketch a right triangle, going from the first point to the second point.
- Count the rise and the run on the legs of the triangle.
- Take the ratio of rise to run to find the slope.
- Graph a Line Given a Point and the Slope
- Plot the given point.
- Use the slope formula
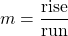 to identify the rise and the run.
to identify the rise and the run. - Starting at the given point, count out the rise and run to mark the second point.
- Connect the points with a line.
- Slope of a Horizontal Line
- The slope of a horizontal line,
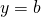 , is 0.
, is 0.
- The slope of a horizontal line,
- Slope of a vertical line
- The slope of a vertical line,
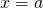 , is undefined
, is undefined
- The slope of a vertical line,
Glossar
- negative slope
- A negative slope of a line goes down as you read from left to right.
- positive slope
- A positive slope of a line goes up as you read from left to right.
- rise
- The rise of a line is its vertical change.
- run
- The run of a line is its horizontal change.
- slope formula
- The slope of the line between two points
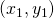 and
and 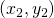 is
is 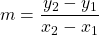 .
.
- slope of a line
- The slope of a line is
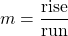 . The rise measures the vertical change and the run measures the horizontal change.
. The rise measures the vertical change and the run measures the horizontal change.
3.4 Exercise Set
In the following exercises, find the slope of each line shown.
|
1.
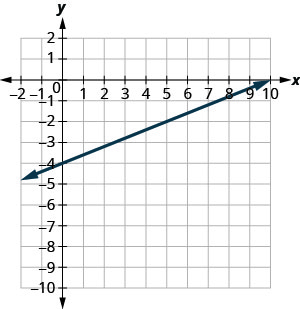 |
2.
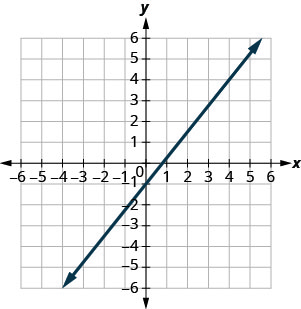 |
|
3.
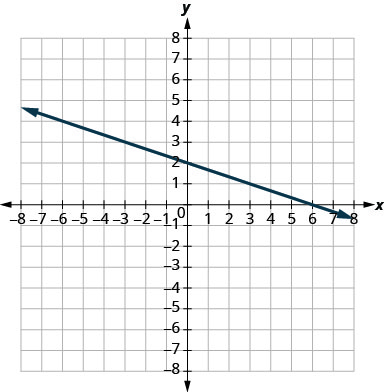 |
4.
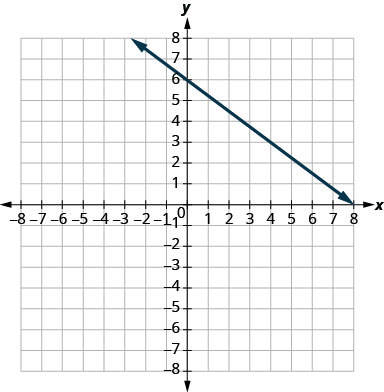 |
|
5.
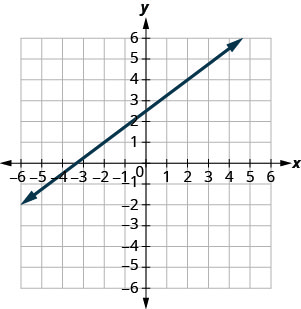 |
6.
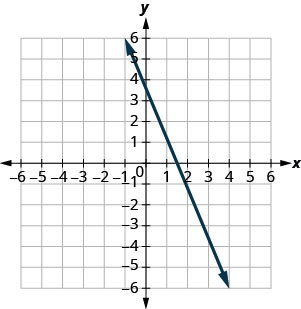 |
|
7.
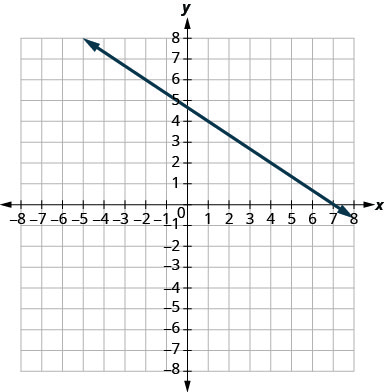 |
8.
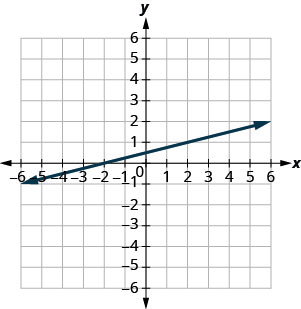 |
In the following exercises, find the slope of each line.
In the following exercises, use the slope formula to find the slope of the line between each pair of points.
In the following exercises, graph each line with the given point and slope.
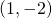 ;
; 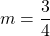
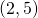 ;
; 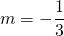
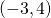 ;
; 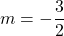
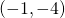 ;
; 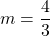
- y-intercept 3;
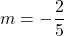
- x-intercept
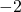 ;
; 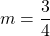
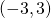 ;
; 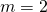
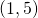 ;
; 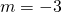
|
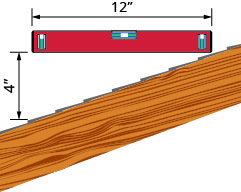
27. An easy way to determine the slope of a roof is to set one end of a 12 inch level on the roof surface and hold it level. Then take a tape measure or ruler and measure from the other end of the level down to the roof surface. This will give you the slope of the roof. Builders, sometimes, refer to this as pitch and state it as an “ a) What is the slope of the roof in this picture? b) What is the pitch in construction terms? |
- A local road has a grade of 6%. The grade of a road is its slope expressed as a percent. Find the slope of the road as a fraction and then simplify. What rise and run would reflect this slope or grade?
- The rules for wheelchair ramps require a maximum 1-inch rise for a 12-inch run.
-
- How long must the ramp be to accommodate a 24-inch rise to the door?
- Create a model of this ramp.
-
Answers


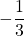
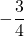

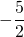
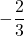

- 0
- undefined
- 0
- undefined


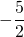
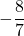

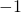
| 19.
|
20.
|
| 21.
|
22.
|
| 23.
|
24.
|
| 25.
|
26.
|
- a)
 b) 4 12 pitch or 4-in-12 pitch
b) 4 12 pitch or 4-in-12 pitch 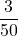 ; rise = 3, run = 50
; rise = 3, run = 50- a) 288 inches (24 feet) b) Models will vary.
Attributions
This chapter has been adapted from “Understand Slope of a Line” in Elementary Algebra (OpenStax) by Lynn Marecek and MaryAnne Anthony-Smith, which is under a CC BY 4.0 Licence. Adapted by Izabela Mazur. See the Adaptation Statement for more information.