9 Financial Mathematics
9.4 Annuities

Learning Objectives
By the end of this section it is expected that you will be able to:
- Distinguish between an ordinary annuity and an annuity due
- Determine the future value of an ordinary annuity
- Determine the payment, given the future value for an ordinary annuity
Annuities
A common financial goal is to be comfortable in retirement. During our working lives we contribute to a retirement fund so that upon retirement we receive a financial payment at regular intervals. Financial transactions that involve a series of equal payments at equal intervals are called annuities. Other examples of annuities include payments on a loan, rental payments, and insurance premiums.
The term of the annuity is the time from the beginning of the first payment interval to the end of the last payment interval. A payment interval is the time between successive payments. If, for example, a vehicle is purchased with monthly payments on a four-year loan then the term of the loan is 4 years and the payment interval is monthly.
In some cases, as with salaries or a senior’s pension, the payments are made at the end of a payment interval. This is referred to as an ordinary annuity. When payments are required at the beginning of a payment interval, as with many loans and mortgages, this is referred to as an annuity due.
It is important to note that the term of the annuity does not necessarily coincide with the first and last payment. Consider a one year loan where 12 equal payments are made on the first of each month. This is an example of an annuity due. The term of the annuity is one year and the payment interval is one month. Refer to Figure 1. There are twelve payments, each occurring on the first day of the month. The first payment is made on Jan. 1 and the last payment is made on Dec. 1. Note that the final payment on Dec. 1 does not occur on the last day of the term of the annuity which is Dec. 31.

Consider a one year loan where 12 equal payments are made on the last day of each month. This is an example of an ordinary annuity. The term of the annuity is one year and the payment interval is one month. Refer to Figure 2. There are twelve payments, each occurring on the last day of the month. The first payment is made on Jan. 31 and the last payment is made on Dec. 31. Note that the first payment on Jan. 31 does not occur on the first day of the term of the annuity which is Jan. 1.

In this section we will only be concerned with ordinary simple annuities. As with all ordinary annuities the payments are made at the end of each payment interval. It is also the case that the compounding interval equals the payment interval. This means that if the payment interval is monthly then interest will also be compounded monthly.
Future Value of an Ordinary Annuity
Consider an investment that is in the form of an ordinary simple annuity. This means that a deposit is made at the end of regular intervals and interest is compounded at each of these intervals. The value of the annuity can grow substantially. The final amount of the annuity is called the future value of the annuity. It is the total of all annuity payments and the accumulated compound interest as illustrated in Figure 3.
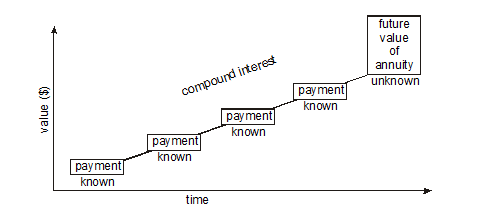
To see how the annuity process works, consider the table in Figure 4 below. This table depicts an ordinary 6-month annuity commencing on Jan. 1 and ending on June 30. The monthly payments are $1000 and the annual interest rate is 6% compounded monthly.
| Month | Balance on the first day of the month | Interest earned during the interval | Deposit at end of the month | Balance at end of the month |
|---|---|---|---|---|
| Jan | $0 | $0 | $1000 | $1000 |
| February | $1000 | $5.00 | $1000 | $2005 |
| March | $2005 | $10.025 = $10.03 | $1000 | $3015.03 |
| April | $3015.03 | $15.075 = $15.08 | $1000 | $4030.11 |
| May | $4030.11 | $20.15 | $1000 | $5050.26 |
| June | $5050.26 | $25.25 | $1000 | $6075.51 |
Fig. 4
Since this is an ordinary annuity the payments are made at the end of the month. Interest is calculated as simple interest I = Prt where r = 0.06 and t = 1/12 year and P = the balance at the beginning of the month.
The first payment of $1000 is deposited at the end of January and therefore no interest is earned for the month of January. At the beginning of February there is $1000 in the account. Interest for the month of February is I = $1000(0.06)(1/12) = $5. At the end of February there will be a deposit of $1000 so the balance at the end of February is $1000 + $5 + $1000 = $2005.
At the beginning of March there is $2005 in the account. Interest for the month of March will be I = $2005(0.06)(1/12) = $10.025 or $10.03 (rounded off). At the end of March $1000 is deposited so the balance at the end of March is $2005 + $$10.03 + $1000 = $3015.03.
At the beginning of April there is $3015.03 in the account. Interest for the month of April will be I = $3015.03(0.06)(1/12) = $15.075 or $15.08 (rounded off). At the end of April $1000 is deposited so the balance at the end of April is $3015.03 + $$15.08 + $1000 = $4030.11.
The process is continued for the remaining two months. At the end of June, the balance will be $6075.51. This is the future value of the annuity, which is the total of all annuity payments and the accumulated compound interest.
Notice that with an ordinary annuity the interest calculation is based on the balance at the beginning of the interval. Since the first payment does not occur until the end of the first payment interval there will not be any interest in the first payment interval. Although the term of the annuity is six months there will only be five intervals where interest is calculated.
With an annuity due the payment would be made at the beginning of each payment interval so for a six month term there would be six interest calculations. Since many loans are set up as an annuity due it is advantageous to the lending institution (but not to the loan recipient).
The calculation of the future value of an annuity can be very time consuming. Fortunately there is a formula for this.
Ordinary Annuity Formula
The ordinary annuity formula is:
| where | A = amount of annuity (Future Value)
P = periodic payment amount r = annual interest rate n = number of compounding periods per year t = time (in years) |
It is important to note that there are variations on how the ordinary annuity formula is written. This is due to the way in which the variables are defined. The formula that is provided in this section defines r as the annual interest rate, n as the number of compounding periods per year, and t as the time in years (term of the annuity in years).
EXAMPLE 1
Assume that the formula will be used to calculate the future value of a two year ordinary annuity that offers an annual interest rate of 6%, monthly payments of $1000, and monthly compounding.
Define each of the variables but do not calculate the future value.
Solution
| where | A = amount of annuity (Future Value) = unknown
P = periodic payment amount = $1000 r = annual interest rate = 6% = 0.06 n = number of compounding periods per year = 12 t = time (in years) = 2 years |
Note that the term of the annuity is 2 years. The interest calculation involves monthly compounding so n = 12 since there are 12 compounding periods in a year.
TRY IT 1
Assume that the formula will be used to calculate the future value of a 1 year ordinary annuity that offers an annual interest rate of 3%, semiannual payments of $500, and semiannual compounding.
Define each of the variables but do not calculate the future value.
Show answer
Amount (A) = unknown
Payment (P) = $500
Annual interest rate (r) = 3% = 0.03
Number of compounding period (n) = 2
Time (t) = 1 year
EXAMPLE 2
Assume that the formula will be used to calculate the future value of a 6 month ordinary annuity that offers an annual interest rate of 4.8%, weekly payments of $100, and weekly compounding.
Define each of the variables but do not calculate the future value.
Solution
A = amount of annuity (Future Value) = unknown
P = periodic payment amount = $100
r = annual interest rate = 4.8% = 0.048
n = number of compounding periods per year = 52
t = time (in years) = 0.5 years
Note that although the term of the annuity is 1/2 year, the interest calculation involves weekly compounding so n = 52 since there are 52 compounding periods in a year.
TRY IT 2
Assume that the formula will be used to calculate the future value of a 9 month ordinary annuity that offers an annual interest rate of 5.5%, monthly payments of $200, and monthly compounding.
Define each of the variables but do not calculate the future value.
Show answer
A = unknown
P = $200
r = 5.5%
n = 12
t = 0.75 years
We will now use the formula to calculate the future value of a six month ordinary annuity that offers an annual interest rate of 6%, monthly payments, and monthly compounding.
EXAMPLE 3
Use the annuity formula to find the annuity amount in 6 months if $1000 is deposited monthly at 6% compounded monthly. Compare this answer to the answer obtained in the table in Figure 4.
Solution
|
||
| Replace variables | ||
| Divide and multiply | ||
| Add | ||
| Calculate the power | ||
| Subtract | ||
| Multiply and divide |
The annuity is worth $6075.50. This answer is $0.01 different than in the table in Figure 4 due to rounding off .
TRY IT 3
Use the formula to calculate the future value of a 9 month ordinary annuity at an annual interest rate of 3%, monthly payments of $50, and monthly compounding.
Show answer
Future value = $454.53
EXAMPLE 4
Use the annuity formula to find the annuity amount in 4 years if $500 is deposited semiannually at 3.6% compounded semiannually.
Solution
|
||
| Replace variables | ||
| Divide and multiply | ||
| Add | ||
| Calculate the power | ||
| Subtract | ||
| Multiply and divide |
The annuity is worth $4261.28.
TRY IT 4
Use the formula to calculate the future value of a 5 year ordinary annuity that offers an annual interest rate of 4.8%, semiannual payments of $4000, and semiannual compounding.
Show answer
Future value = $44,608.43
The future value or annuity amount includes all payments and compound interest. To determine the total interest we must subtract the total value of all annuity payments from the future value of the annuity.
Interest on an Annuity
Interest on an Annuity =
Future Value of the Annuity – Total Value of the Payments =
Future Value of the Annuity – (Payment amount × number of payments per year × number of years)
EXAMPLE 5
Consider Example 3. For a 6-month annuity where $1000 is deposited monthly the value of the annuity at the end of 6 months is 6075.51. Determine the total interest earned on the annuity.
Solution
Interest Earned = Future Value of the Annuity – Total Value of the Payments (Deposits) = $6075.51 – ($1000 x 6 payments) = $75.51.
Refer to the table in Figure 4 to confirm that the column “interest earned” adds to this identical amount.
TRY IT 5
Refer to Try It 3. For a 9 month ordinary annuity with monthly payments of $50, determine the total interest earned on the annuity.
Show answer
Future value = $4.53
EXAMPLE 6
a) How much would an annuity be worth in 2 years at 2.4% compounded monthly if the periodic payments are $40 per month?
b) Determine the total interest earned on the annuity.
Solution:
a)
|
|
The annuity is worth $982.41 after 2 years.
b) The total interest earned is: $982.41 – ($40 × 12payments/yr × 2yr) = $982.41 – $960 = $22.41
TRY IT 6
Consider a ten-year ordinary annuity that offers an annual interest rate of 4.5%, semiannual payments of $1000, and semiannual compounding
a) How much would the annuity be worth in 10 years?
b) Determine the total interest earned on the annuity.
Show answer
Future value = $24911.52
Interest = $24911.52 – ($1000)(10 years)(2 payments/year) = $24911.52 – $20000 = $4911.52
EXAMPLE 7
Tish plans to go back to university and opens an account into which she will deposit $300 at the end of every month for 4 years. The account offers an annual interest rate of 4.8% compounded monthly. Assuming a fixed interest rate and no additional deposits or withdrawals, how much will be in the account at the end of 4 years? How much interest will Tish earn in the 4 years?
Solution
|
|
| Interest | |
TRY IT 7
A credit union is offering 6.8% compounded monthly on a savings account. If you deposit $100 at the end of every month for two years (assume no withdrawals) how much will be in the account at the end of two years? How much interest will you earn?
Show answer
Amount in 2 years = $2563.10
Interest = $2563.10 – ($100)(2 years)(12 payments/year) = $163.10
Determining the Annuity Payment
Businesses and individuals often wish to accumulate a certain amount of money by making regular deposits (payments) into an annuity. Perhaps an individual or business wishes to purchase a larger ticket item such as an appliance or a piece of equipment in one year’s time. Rather than taking out a loan they could choose to deposit a specific amount every month so as to accumulate the required funds by the end of the one year. The amount that needs to be deposited is represented by the payment in the annuity formula. The formula must be solved for the payment (P).
Periodic Payment Formula
The periodic payment formula is:
| P = periodic payment amount | |
| A = annuity amount | |
| r = annual interest rate | |
| n = number of times interest is calculated in a year | |
| t = time (in years) |
EXAMPLE 8
A home bakery wants to purchase a new oven in one year’s time. The oven is estimated to cost $5000. The baker has found an account that offers 3.2% monthly compounding.
a) How much must be deposited at the end of each month to accumulate to the $5000?
b) What is the total amount that the baker deposits over the one year?
c) How much of the $5000 is interest?
Solution
| P = ?
A = $5000 r = 3.2% = 0.032 t = 1 n = 12
|
|
a) The baker must deposit $410.59 per month.
b) The baker deposits $410.59/mth × 12 months = $4927.08 in one year.
c) Since there is $5000 in the account at the end of the year, the interest component will be:
$5000 – $4927.09 = $72.91
TRY IT 8
Cara is saving to start college in three years and hopes to have saved $12,000 in three years. She opens an account offering 4.8% compounded monthly.
a) How much must Cara deposit at the end of each month to accumulate to the $12000?
b) What is the total amount that Cara deposits over the three years?
c) How much of the $12,000 is interest?
Show answer
a) Monthly deposit must be $310.57 b) Total deposited is $11,180.67 c) $819.33
EXAMPLE 9
Sara hopes to accumulate $140,000 in 12 years. She has found an annuity that offers 8% annual compounding and requires that she make a deposit at the end of each year.
a) How much must Sara deposit at the end of each year to accumulate to the $140,000?
b) What is the total amount that Sara deposits over the twelve years?
c) How much of the $140,000 is interest?
Solution:
a)
| P = ?
A = $140,000 r = 8% = 0.08 t = 12 n = 1
|
|
Sara must deposit $7,377.30 per year
b) 12 years × $7377.30/yr = $88527.60
c) Interest = $140000 – $88527.60 = $51472.40
TRY IT 9
Zach is saving to go on a trip in one year’s time. He hopes to have $3200 at the end of one year so he makes monthly deposits into an account offering 2.4% compounded monthly.
a) How much must Zach deposit at the end of each month to accumulate to the $3200?
b) What is the total amount that Zach deposits over the twelve months?
c) How much of the $3200 is interest?
Show answer
a) Monthly deposit must be $263.75 b) $3165 c) $35
EXAMPLE 10
What monthly payment is necessary for an annuity to be worth $10,000 in 3 years at 7% compounded monthly?
Solution
| P = ?
A = $10,000 r = 7% = 0.07 t = 3 |
||
| n = 12 | Replace variables with their values | |
| Divide 0.07 by 12 | ||
| Multiply and calculate the power | ||
The periodic payment is $250.44
TRY IT 10
Zach has become more ambitious and is saving to go on world cruise in four years. He anticipates that the cruise will cost $38,000. How much will he need to deposit each month in an account offering 3.6% compounded monthly to accumulate to $38, 000 in four years?
Show answer
$737.22/month
Key Concepts
- to determine the future value of an ordinary annuity (A):
![]()
- to determine the interest earned on an annuity:
Interest on an Annuity =
Future Value of the Annuity – Total Value of the Payments
- to determine the payment, given the future value for an ordinary annuity:
![]()
Glossary
annuity
is a series of payments made at fixed intervals.
annuity due
is an annuity where the payment is due at the beginning of each payment period.
future value of the annuity
is the final amount of the annuity. It is the total of all annuity payments and the accumulated compound interest.
ordinary annuity
is an annuity where the payment is due at the end of each payment period.
payment interval
is the time between successive annuity payments.
term of the annuity
is the time from the beginning of the first payment interval to the end of the last payment interval.
Exercise Set 9.4
-
- Complete the table below for an ordinary annuity, where $2000 is deposited annually for 5 years at 5% compounded annually.
Year Amount at start of the year Interest earned Annual deposit at end of the year Amount at end of the year 1 — — $2000 $2000 2 $2000 $100 $2000 $4100 3 $4100 4 5 - Use the ordinary annuity formula to calculate the amount at the end of the 5-year term. Do your formula and table amounts agree?
- Complete the table below for an ordinary annuity, where $2000 is deposited annually for 5 years at 5% compounded annually.
- Assume that the formula will be used to calculate the future value of an ordinary annuity for the information provided. For each of these state: the payment amount (P), the time in years (t), the number of compounding periods (n) and the interest rate (r). Do not actually calculate the future value.
- A three year ordinary annuity that offers an annual interest rate of 2.8%, with semiannual deposits of $1500 and semiannual compounding.
- An 8 month ordinary annuity that offers an annual interest rate of 4.6%, with monthly deposits of $180 and monthly compounding.
- Find the future value of an ordinary annuity when
- A periodic payment of $1000 per year earns 8% compounded annually for 10 years
- A payment of $100 per month earns 4% compounded monthly for 5 years
- A payment of $200 quarterly earns 3.82% compounded quarterly for 7 years
- Daniel contributes $100 per month into an investment that earns 6% compounded monthly. How much money would Daniel have in:
- 1 year?
- 2 years?
- 5 years?
- 10 years?
- The Andersons plan to retire in 25 years and want to start saving for it now. They hope to be able to earn about 10% compounded annually. Determine the amount of their annuity if they make the following periodic payments.
- $500 per year
- $1000 per year
- $2000 per year
- $3500 per year
- The Mitchells are choosing between two ordinary annuities. They have the choice of either contributing $1200 a year at 10% compounded annually for 25 years or contributing $100 per month at 10% compounded monthly for 25 years.
- How much would the Mitchells have in 25 years if they make annual contributions?
- How much would the Mitchells have in 25 years if they make monthly contributions?
- Which investment (yearly or monthly) would earn the greater amount and by how much?
- The Gardners plan to save for their child’s education by depositing $40 a month into a special savings plan which pays 8% compounded monthly.
- How much would the annuity be worth after 1 year?
- How much after 18 years?
- Imagine you start saving for your retirement and contribute $1000 yearly and average 6.4% compounded annually. The amount of the annuity depends on the length of the annuity. Complete the table below.
Years Annuity amount 10 15 20 25 30 - In question 8 above, what is the effect of saving for your retirement over a 30 year period as opposed to a 10 year period?
- Find the periodic payment needed to accumulate to an annuity amount of:
- $1000 at 5% compounded monthly for 1 year
- $20,000 at 10% compounded yearly for 15 years
- $5000 at 8% compounded quarterly for 3 years
- Mike wants to buy a $1500 stereo 9 months from now. How much will he have to deposit every month into a savings plan paying 6.5% compounded monthly?
- You would like to save $3500 in two years. What monthly payment would you have to make if your investment can earn 5% compounded monthly?
- The Wests need $60000 for their child’s education 6 years from now. How much should they put aside every month if they hope to earn 4% compounded monthly?
- Paul wants to save $20,000 in order to purchase a vehicle in 4 years time. He plans to make equal monthly contributions for 4 years. He found an annuity offering 2.6% compounded monthly and was about to commit but then found another option offering 3.4% compounded monthly.
- Determine the monthly payments for each of the two options.
- Determine the total amount of money that Paul saved for other uses by finding the account offering 3.4%.
- Imagine you wanted to be a millionaire 30 years from now. How much would you have to contribute to an ordinary annuity every year if you think you could earn 12% compounded yearly?
Answers
-
-
Start Date Amount at start of the year Interest earned Annual deposit at end of the year Amount at end of the year 1 — — $2000 $2000 2 $2000 $100 $2000 $4100 3 $4100 $205 $2000 $6305 4 $6305 $315.25 $2000 $8620.25 5 $8620.25 $431.0125 $2000 $11051.26 - $11,051.26 The answers should be the same.
-
-
- P = $1500 t = 3 years n = 2 r = 2.8% = 0.028
- P = $180 t = 2/3 years n = 12 r = 4.6% = 0.046
-
- $14 486.56
- $6629.90
- $6385.47
-
- $1233.56
- $2543.20
- $6977.00
- $16 387.93
-
- $49 173.53
- $98 347.06
- $196 694.12
- $344 214.71
-
- $118 016.47
- $132 683.33
- Monthly by $14 666.87
-
- $498.00
- $19 203.45
-
Years Annuity Amount 10 $13431.03 15 $23997.73 20 $38407.19 25 $58056.88 30 $84852.51 - The annuity is worth (
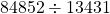 ) over 6 times more
) over 6 times more -
- $81.44/month
- $629.48 per year
- $372.80 per quarter
- $163.09 per month
- $138.97 per month
- $738.71 per month
-
- For the 2.6% account payments of $395.83/mth; For the 3.4% account payments of $389.56/mth
- 48 months of saving a difference of $6.27 provided $300.96 extra for Paul
- $4143.65 per year
Attribution
Some of the content for this chapter is from “Unit 6: Ordinary annuities” and “Unit 7: Annuity payments” in Financial Mathematics by Paul Grinder, Velma McKay, Kim Moshenko, and Ada Sarsiat, which is under a CC BY 4.0 Licence.. Adapted by Kim Moshenko. See the Copyright page for more information.

