1. Operations with Real Numbers
1.2 Integers
Learning Objectives
By the end of this section it is expected that you will be able to:
- Use negatives and opposites
- Simplify: expressions with absolute value
- Add ans subtract integers
- Multiply and divide integers
- Simplify Expressions with Integers
Use Negatives and Opposites
If you have ever experienced a temperature below zero or accidentally overdrawn your checking account, you are already familiar with negative numbers. Negative numbers are numbers less than ![]() . The negative numbers are to the left of zero on the number line. See Figure 1.
. The negative numbers are to the left of zero on the number line. See Figure 1.
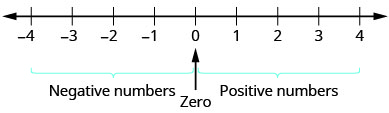
The arrows on the ends of the number line indicate that the numbers keep going forever. There is no biggest positive number, and there is no smallest negative number.
Is zero a positive or a negative number? Numbers larger than zero are positive, and numbers smaller than zero are negative. Zero is neither positive nor negative.
Consider how numbers are ordered on the number line. Going from left to right, the numbers increase in value. Going from right to left, the numbers decrease in value. See Figure 2.
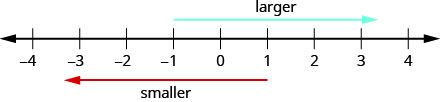
Remember that we use the notation:
a < b (read “a is less than b”) when a is to the left of b on the number line.
a > b (read “a is greater than b”) when a is to the right of b on the number line.
Now we need to extend the number line which showed the whole numbers to include negative numbers, too. The numbers marked by points in Figure 3 are called the integers. The integers are the numbers ![]()

EXAMPLE 1
Order each of the following pairs of numbers, using < or >: a) ![]() ___
___![]() b)
b) ![]() ___
___![]() c)
c) ![]() ___
___![]() d)
d) ![]() ___
___![]() .
.
It may be helpful to refer to the number line shown.

| a) 14 is to the right of 6 on the number line. | |
| b) −1 is to the left of 9 on the number line. | |
| c) −1 is to the right of −4 on the number line. | |
| d) 2 is to the right of −20 on the number line. |
TRY IT 1
Order each of the following pairs of numbers, using < or > ![]() a)
a) ![]() ___
___![]() b)
b) ![]() ___
___![]() c)
c) ![]() ___
___![]() d)
d) ![]() ___
___![]() .
.
Show answer
a) > b) < c) > d) >
You may have noticed that, on the number line, the negative numbers are a mirror image of the positive numbers, with zero in the middle. Because the numbers 2 and ![]() are the same distance from zero, they are called opposites. The opposite of 2 is
are the same distance from zero, they are called opposites. The opposite of 2 is ![]() , and the opposite of
, and the opposite of ![]() is 2
is 2
Opposite
The opposite of a number is the number that is the same distance from zero on the number line but on the opposite side of zero.
(Figure 4) illustrates the definition.

Opposite Notation
![]() means the opposite of the number a.
means the opposite of the number a.
The notation ![]() is read as “the opposite of a.”
is read as “the opposite of a.”
The whole numbers and their opposites are called the integers. The integers are the numbers ![]()
Integers
The whole numbers and their opposites are called the integers.
The integers are the numbers
Simplify: Expressions with Absolute Value
We saw that numbers such as ![]() are opposites because they are the same distance from 0 on the number line. They are both two units from 0. The distance between 0 and any number on the number line is called the absolute value of that number.
are opposites because they are the same distance from 0 on the number line. They are both two units from 0. The distance between 0 and any number on the number line is called the absolute value of that number.
Absolute Value
The absolute value of a number is its distance from 0 on the number line.
The absolute value of a number n is written as ![]() .
.
For example,
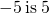 units away from
units away from 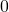 , so
, so 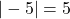 .
. units away from
units away from 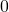 , so
, so 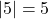 .
.
Figure 5 illustrates this idea.
The integers ![]() units away from
units away from ![]() .
.
The absolute value of a number is never negative (because distance cannot be negative). The only number with absolute value equal to zero is the number zero itself, because the distance from ![]() on the number line is zero units.
on the number line is zero units.
Property of Absolute Value
![]() for all numbers
for all numbers
Absolute values are always greater than or equal to zero!
Mathematicians say it more precisely, “absolute values are always non-negative.” Non-negative means greater than or equal to zero.
EXAMPLE 2
Simplify: a) ![]() b)
b) ![]() c)
c) ![]() .
.
The absolute value of a number is the distance between the number and zero. Distance is never negative, so the absolute value is never negative.
a) ![]()
![]()
b) ![]()
![]()
c) ![]()
![]()
TRY IT 2
Simplify: a) ![]() b)
b) ![]() c)
c) ![]() .
.
Show answer
a) 4 b) 28 c) 0
In the next example, we’ll order expressions with absolute values. Remember, positive numbers are always greater than negative numbers!
EXAMPLE 3
Fill in <, >, ![]() for each of the following pairs of numbers:
for each of the following pairs of numbers:
a) ![]() ___
___![]() b)
b) ![]() ___
___![]() c)
c) ![]() ___
___![]() d) –
d) –![]() ___
___![]()
| a) Simplify. Order. |
5 ___ -5 |
| 5 > -5 | |
| b) Simplify. Order. |
|
| 8 ___ -8 | |
| 8 > -8 | |
| 8 > – |
|
| c) Simplify. Order. |
9 ___ – -9 ___ -9 -9 = -9 -9 = – |
| d) Simplify. Order. |
– 16 ____ -16 16 > -16 – |
TRY IT 3
Fill in <, >, or ![]() for each of the following pairs of numbers: a)
for each of the following pairs of numbers: a) ![]() ___-
___-![]() b)
b) ![]() ___-
___-![]() c)
c) ![]() ___
___![]()
d) ![]() ___
___![]() .
.
Show answer
a) > b) > c) < d) >
We now add absolute value bars to our list of grouping symbols. When we use the order of operations, first we simplify inside the absolute value bars as much as possible, then we take the absolute value of the resulting number.
| Parentheses | ( ) |
| Brackets | [ ] |
| Braces | { } |
| Absolute value | | | |
In the next example, we simplify the expressions inside absolute value bars first, just like we do with parentheses.
EXAMPLE 4
Simplify: ![]() .
.
| Work inside parentheses first: subtract 2 from 6. | |
| Multiply 3(4). | |
| Subtract inside the absolute value bars. | |
| Take the absolute value. | |
| Subtract. |
TRY IT 4
Simplify: ![]() .
.
Show answer
16
Add Integers
Most students are comfortable with the addition and subtraction facts for positive numbers. But doing addition or subtraction with both positive and negative numbers may be more challenging.
We will use two colour counters to model addition and subtraction of negatives so that you can visualize the procedures instead of memorizing the rules.
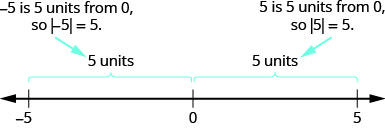
We let one colour (blue) represent positive. The other colour (red) will represent the negatives. If we have one positive counter and one negative counter, the value of the pair is zero. They form a neutral pair. The value of this neutral pair is zero.
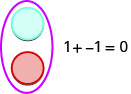
We will use the counters to show how to add the four addition facts using the numbers ![]() and
and ![]() .
.
![]()
The first example adds 5 positives and 3 positives—both positives.
The second example adds 5 negatives and 3 negatives—both negatives.
In each case we got 8—either 8 positives or 8 negatives.
When the signs were the same, the counters were all the same color, and so we added them.

So what happens when the signs are different? Let’s add ![]() and
and ![]() .
.
When we use counters to model addition of positive and negative integers, it is easy to see whether there are more positive or more negative counters. So we know whether the sum will be positive or negative.
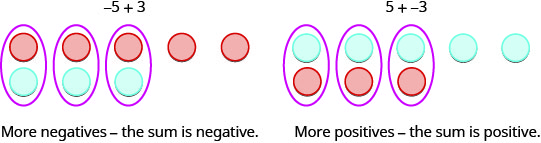
EXAMPLE 5
Add: a) ![]() b)
b) ![]() .
.
a)
| −1 + 5 | |
 |
|
| There are more positives, so the sum is positive. | 4 |
b)
| 1 + (−5) | |
 |
|
| There are more negatives, so the sum is negative. | −4 |
TRY IT 5
Add: a) ![]() b)
b) ![]() .
.
Show answer
a) 2 b) ![]()
Now that we have added small positive and negative integers with a model, we can visualize the model in our minds to simplify problems with any numbers.
When you need to add numbers such as ![]() , you really don’t want to have to count out 37 blue counters and 53 red counters. With the model in your mind, can you visualize what you would do to solve the problem?
, you really don’t want to have to count out 37 blue counters and 53 red counters. With the model in your mind, can you visualize what you would do to solve the problem?
Picture 37 blue counters with 53 red counters lined up underneath. Since there would be more red (negative) counters than blue (positive) counters, the sum would be negative. How many more red counters would there be? Because ![]() , there are 16 more red counters.
, there are 16 more red counters.
Therefore, the sum of ![]() is
is ![]() .
.
Let’s try another one. We’ll add ![]() . Again, imagine 74 red counters and 27 more red counters, so we’d have 101 red counters. This means the sum is
. Again, imagine 74 red counters and 27 more red counters, so we’d have 101 red counters. This means the sum is ![]() .
.
![]()
Let’s look again at the results of adding the different combinations of ![]() and
and ![]() .
.
Addition of Positive and Negative Integers
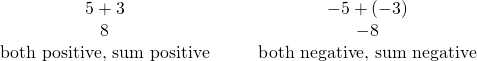
When the signs are the same, the counters would be all the same color, so add them.
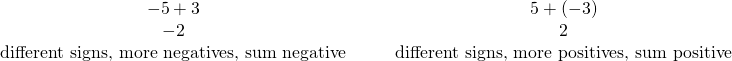
When the signs are different, some of the counters would make neutral pairs, so subtract to see how many are left.
Visualize the model as you simplify the expressions in the following examples.
EXAMPLE 6
Simplify: a) ![]() b)
b) ![]() .
.
- Since the signs are different, we subtract
 The answer will be negative because there are more negatives than positives.
The answer will be negative because there are more negatives than positives.
- Since the signs are the same, we add. The answer will be negative because there are only negatives.
TRY IT 6
Simplify: a) ![]() b)
b) ![]() .
.
Show answer
a)![]() b)
b)![]()
The techniques used up to now extend to more complicated problems, like the ones we’ve seen before. Remember to follow the order of operations!
EXAMPLE 7
Simplify: ![]() .
.
| Simplify inside the parentheses. | |
| Multiply. | |
| Add left to right. |
TRY IT 7
Simplify: ![]() .
.
Show answer
13
Subtract Integers
We will continue to use counters to model the subtraction. Remember, the blue counters represent positive numbers and the red counters represent negative numbers.
Perhaps when you were younger, you read ![]() as
as ![]() take away
take away ![]() When you use counters, you can think of subtraction the same way!
When you use counters, you can think of subtraction the same way!
We will model the four subtraction facts using the numbers ![]() and
and ![]() .
.
The first example, we subtract 3 positives from 5 positives and end up with 2 positives.
In the second example, we subtract 3 negatives from 5 negatives and end up with 2 negatives.
Each example used counters of only one color, and the “take away” model of subtraction was easy to apply.
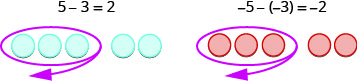
What happens when we have to subtract one positive and one negative number? We’ll need to use both white and red counters as well as some neutral pairs. Adding a neutral pair does not change the value. It is like changing quarters to nickels—the value is the same, but it looks different.
- To subtract
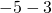 , we restate it as
, we restate it as 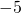 take away 3.
take away 3.
We start with 5 negatives. We need to take away 3 positives, but we do not have any positives to take away.
Remember, a neutral pair has value zero. If we add 0 to 5 its value is still 5. We add neutral pairs to the 5 negatives until we get 3 positives to take away.
| −5 − 3 means −5 take away 3. | |
| We start with 5 negatives. |  |
| We now add the neutrals needed to get 3 positives. |  |
| We remove the 3 positives. | 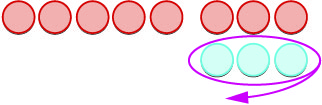 |
| We are left with 8 negatives. |  |
| The difference of −5 and 3 is −8. | −5 − 3 = −8 |
And now, the fourth case, ![]() . We start with 5 positives. We need to take away 3 negatives, but there are no negatives to take away. So we add neutral pairs until we have 3 negatives to take away.
. We start with 5 positives. We need to take away 3 negatives, but there are no negatives to take away. So we add neutral pairs until we have 3 negatives to take away.
| 5 − (−3) means 5 take away −3. | |
| We start with 5 positives. |  |
| We now add the needed neutrals pairs. |  |
| We remove the 3 negatives. | 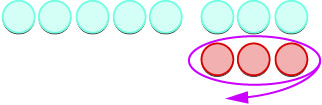 |
| We are left with 8 positives. |  |
| The difference of 5 and −3 is 8. | 5 − (−3) = 8 |
EXAMPLE 8
Subtract: a) ![]() b)
b) ![]() .
.
a)
| Take 1 positive from the one added neutral pair. |   |
−3 − 1
−4 |
b)
| Take 1 negative from the one added neutral pair. |   |
3 − (−1)
4 |
TRY IT 8
Subtract: a) ![]() b)
b) ![]() .
.
Show answer
a) ![]() b) 10
b) 10
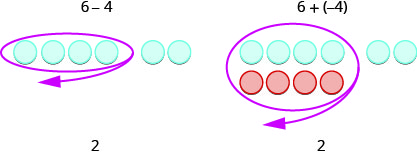
Have you noticed that subtraction of signed numbers can be done by adding the opposite? In Example 8, ![]() is the same as
is the same as ![]() and
and ![]() is the same as
is the same as ![]() . You will often see this idea, the subtraction property, written as follows:
. You will often see this idea, the subtraction property, written as follows:
Subtraction Property
Look at these two examples.
Of course, when you have a subtraction problem that has only positive numbers, like ![]() , you just do the subtraction. You already knew how to subtract
, you just do the subtraction. You already knew how to subtract ![]() long ago. But knowing that
long ago. But knowing that ![]() gives the same answer as
gives the same answer as ![]() helps when you are subtracting negative numbers. Make sure that you understand how
helps when you are subtracting negative numbers. Make sure that you understand how ![]() and
and ![]() give the same results!
give the same results!
Look at what happens when we subtract a negative.

Subtracting a negative number is like adding a positive!
You will often see this written as ![]() .
.
What happens when there are more than three integers? We just use the order of operations as usual.
EXAMPLE 9
Simplify: ![]() .
.
| Simplify inside the parentheses first. | |
| Subtract left to right. | |
| Subtract. |
TRY IT 9
Simplify: ![]() .
.
Show answer
3
Multiply Integers
Since multiplication is mathematical shorthand for repeated addition, our model can easily be applied to show multiplication of integers. Let’s look at this concrete model to see what patterns we notice. We will use the same examples that we used for addition and subtraction. Here, we will use the model just to help us discover the pattern.
We remember that ![]() means add a, b times. Here, we are using the model just to help us discover the pattern.
means add a, b times. Here, we are using the model just to help us discover the pattern.
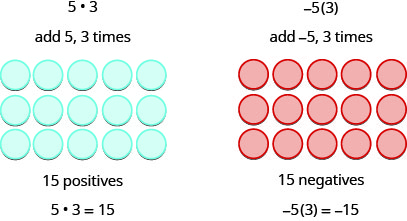
The next two examples are more interesting.
What does it mean to multiply 5 by ![]() It means subtract 5, 3 times. Looking at subtraction as “taking away,” it means to take away 5, 3 times. But there is nothing to take away, so we start by adding neutral pairs on the work space. Then we take away 5 three times.
It means subtract 5, 3 times. Looking at subtraction as “taking away,” it means to take away 5, 3 times. But there is nothing to take away, so we start by adding neutral pairs on the work space. Then we take away 5 three times.
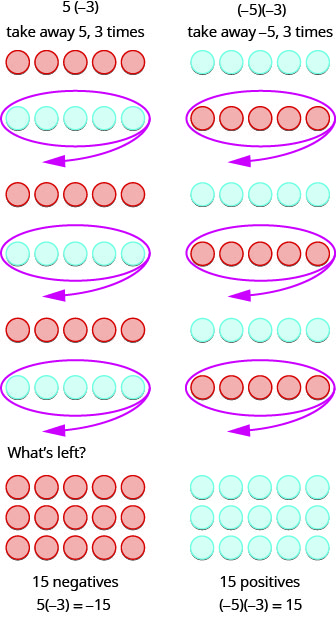
In summary:
Notice that for multiplication of two signed numbers, when the:
- signs are the same, the product is positive.
- signs are different, the product is negative.
We’ll put this all together in the chart below
Multiplication of Signed Numbers
For multiplication of two signed numbers:
| Same signs | Product | Example |
|---|---|---|
| Two positives Two negatives |
Positive Positive |
| Different signs | Product | Example |
| Positive \cdot negative Negative \cdot positive |
Negative Negative |
EXAMPLE 10
Multiply: a) ![]() b)
b) ![]() c)
c) ![]() d)
d) ![]() .
.
| a) Multiply, noting that the signs are different so the product is negative. |
|
| b) Multiply, noting that the signs are the same so the product is positive. |
|
| c) Multiply, with different signs. |
|
| d) Multiply, with same signs. |
TRY IT 10
Multiply: a) ![]() b)
b) ![]() c)
c) ![]() d)
d) ![]() .
.
Show answer
a)![]() b) 28 c)
b) 28 c) ![]() d) 60
d) 60
When we multiply a number by 1, the result is the same number. What happens when we multiply a number by ![]() ? Let’s multiply a positive number and then a negative number by
? Let’s multiply a positive number and then a negative number by ![]() to see what we get.
to see what we get.
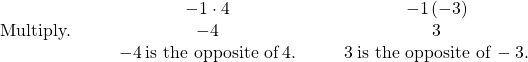
Each time we multiply a number by ![]() , we get its opposite!
, we get its opposite!
Multiplication by ![]()
![]()
Multiplying a number by ![]() gives its opposite.
gives its opposite.
EXAMPLE 11
Multiply: a) ![]() b)
b) ![]() .
.
| a) Multiply, noting that the signs are different so the product is negative. |
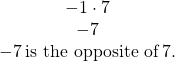 |
| b) Multiply, noting that the signs are the same so the product is positive. |
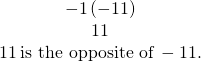 |
TRY IT 11
Multiply: a) ![]() b)
b) ![]() .
.
Show answer
a)![]() b) 17
b) 17
Divide Integers
What about division? Division is the inverse operation of multiplication. So, ![]() because
because ![]() . In words, this expression says that 15 can be divided into three groups of five each because adding five three times gives 15. Look at some examples of multiplying integers, to figure out the rules for dividing integers.
. In words, this expression says that 15 can be divided into three groups of five each because adding five three times gives 15. Look at some examples of multiplying integers, to figure out the rules for dividing integers.
![]()
Division follows the same rules as multiplication!
For division of two signed numbers, when the:
- signs are the same, the quotient is positive.
- signs are different, the quotient is negative.
And remember that we can always check the answer of a division problem by multiplying.
Multiplication and Division of Signed Numbers
For multiplication and division of two signed numbers:
- If the signs are the same, the result is positive.
- If the signs are different, the result is negative.
| Same signs | Result |
|---|---|
| Two positives | Positive |
| Two negatives | Positive |
If the signs are the same, the result is positive.
| Different signs | Result |
|---|---|
| Positive and negative | Negative |
| Negative and positive | Negative |
If the signs are different, the result is negative.
EXAMPLE 12
Divide: a) ![]() b)
b) ![]() .
.
| a) Divide. With different signs, the quotient is negative. |
|
| b) Divide. With signs that are the same, the quotient is positive. |
TRY IT 12
Divide: a) ![]() b)
b) ![]() .
.
Show answer
a)![]() b) 39
b) 39
Simplify Expressions with Integers
What happens when there are more than two numbers in an expression? The order of operations still applies when negatives are included. Remember My Dear Aunt Sally?
Let’s try some examples. We’ll simplify expressions that use all four operations with integers—addition, subtraction, multiplication, and division. Remember to follow the order of operations.
EXAMPLE 13
Simplify: ![]() .
.
| Multiply first. | |
| Add. | |
| Subtract. |
TRY IT 13
Simplify: ![]() .
.
Show answer
![]()
EXAMPLE 14
Simplify: a) ![]() b)
b) ![]() .
.
| a) Write in expanded form. Multiply. Multiply. Multiply. |
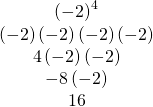 |
| b) Write in expanded form. We are asked to find the opposite of Multiply. Multiply. Multiply. |
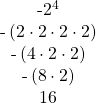 |
Notice the difference in parts a) and b). In part a), the exponent means to raise what is in the parentheses, the ![]() to the
to the ![]() power. In part b), the exponent means to raise just the 2 to the
power. In part b), the exponent means to raise just the 2 to the ![]() power and then take the opposite.
power and then take the opposite.
TRY IT 14
Simplify: a) ![]() b)
b) ![]() .
.
Show answer
a) 81 b) ![]()
The next example reminds us to simplify inside parentheses first.
EXAMPLE 15
Simplify: ![]() .
.
| Subtract in parentheses first. | |
| Multiply. | |
| Subtract. |
TRY IT 15
Simplify: ![]() .
.
Show answer
29
EXAMPLE 16
Simplify: ![]() .
.
| Exponents first. | |
| Multiply. | |
| Divide. |
TRY IT 16
Simplify: ![]() .
.
Show answer
4
EXAMPLE 17
Simplify: ![]() .
.
| Multiply and divide left to right, so divide first. | |
| Multiply. | |
| Add. |
TRY IT 17
Simplify: ![]() .
.
Show answer
21
Access these online resources for additional instruction and practice with adding and subtracting integers. You will need to enable Java in your web browser to use the applications.
Key Concepts
- Addition of Positive and Negative Integers
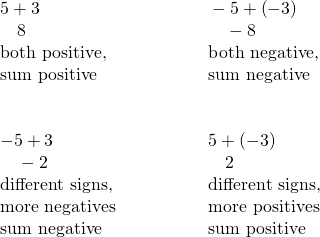
- Property of Absolute Value:
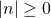 for all numbers. Absolute values are always greater than or equal to zero!
for all numbers. Absolute values are always greater than or equal to zero! - Subtraction of Integers
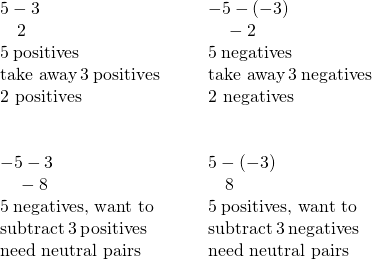
- Subtraction Property: Subtracting a number is the same as adding its opposite.
- Multiplication and Division of Two Signed Numbers
- Same signs—Product is positive
- Different signs—Product is negative
Glossary
- absolute value
- The absolute value of a number is its distance from 0 on the number line. The absolute value of a number
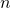 is written as
is written as  .
.
- integers
- The whole numbers and their opposites are called the integers: …−3, −2, −1, 0, 1, 2, 3…
- opposite
- The opposite of a number is the number that is the same distance from zero on the number line but on the opposite side of zero:
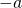 means the opposite of the number. The notation
means the opposite of the number. The notation 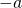 is read “the opposite of
is read “the opposite of  .”
.”
1.2 Exercise Set
In the following exercises, order each of the following pairs of numbers, using < or >.
-
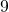 ___
___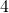
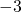 ___
___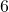
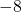 ___
___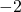
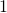 ___
___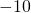
In the following exercises, simplify.
In the following exercises, fill in <, >, or ![]() for each of the following pairs of numbers.
for each of the following pairs of numbers.
-
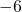 ___
___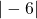
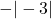 ___
___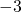
In the following exercises, simplify.
In the following exercises, simplify each expression.
In the following exercises, simplify.
In the following exercises, simplify each expression.
In the following exercises, multiply.
In the following exercises, divide.
In the following exercises, simplify each expression.
In the following exercises, solve.
- Temperature On January
 , the high temperature in Lytton, British Columbia, was
, the high temperature in Lytton, British Columbia, was 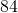 ° . That same day, the high temperature in Fort Nelson, British Columbia was
° . That same day, the high temperature in Fort Nelson, British Columbia was 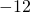 °. What was the difference between the temperature in Lytton and the temperature in Embarrass?
°. What was the difference between the temperature in Lytton and the temperature in Embarrass? - Checking Account Ester has $124 in her checking account. She writes a check for $152. What is the new balance in her checking account?
- Checking Account Kevin has a balance of
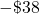 in his checking account. He deposits $225 to the account. What is the new balance?
in his checking account. He deposits $225 to the account. What is the new balance? -
Provincial budgets For 2019 the province of Quebec estimated it would have a budget surplus of $5.6 million. That same year, Alberta estimated it would have a budget deficit of $7.5 million.
Use integers to write the budget of:
- Quebec
- Alberta
Answers:
-
- >
- <
- <
- >
-
- 32
- 0
- 16
-
- <
- =
- 56
- 0
- 8
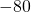
- 32
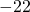
- 108
- 29
- 6
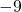
- 12
-
- 16
- 16
-
- 45
- 45
- 27
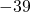
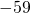
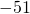
- -99
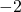
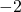
- 22
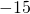
- 4
- 6
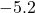
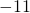
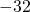
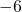
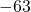
- 14
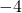
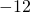
- 13
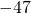
- 64
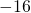
- 90
- 9
- 41
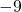
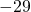
- 5
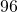 °
°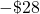
- $187
-
- $5.6 million
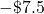 million
million
Attributions
This chapter has been adapted from “Add and Subtract Integers” in Elementary Algebra (OpenStax) by Lynn Marecek and MaryAnne Anthony-Smith, which is under a CC BY 4.0 Licence. Adapted by Izabela Mazur. See the Copyright page for more information.

