1. Operations with Real Numbers
1.3 Fractions
Learning Objectives
By the end of this section it is expected that you will be able to:
- Multiply and divide fractions
- Simplifying expressions with fraction bar
- Add or subtract fractions with a common denominator
- Add or subtract fractions with different denominators
- Use the order of operations to simplify complex fractions
Multiply Fractions
Many people find multiplying and dividing fractions easier than adding and subtracting fractions. So we will start with fraction multiplication.
We’ll use a model to show you how to multiply two fractions and to help you remember the procedure. Let’s start with ![]() .
.

Now we’ll take ![]() of
of ![]() .
.

Notice that now, the whole is divided into 8 equal parts. So ![]() .
.
To multiply fractions, we multiply the numerators and multiply the denominators.
Fraction Multiplication
If ![]() are numbers where
are numbers where ![]() , then
, then
![]()
To multiply fractions, multiply the numerators and multiply the denominators.
When multiplying fractions, the properties of positive and negative numbers still apply, of course. It is a good idea to determine the sign of the product as the first step. In Example 1, we will multiply negative and a positive, so the product will be negative.
EXAMPLE 1
Multiply: ![]() .
.
The first step is to find the sign of the product. Since the signs are the different, the product is negative.
| Determine the sign of the product; multiply. | |
| Are there any common factors in the numerator and the demoninator? No. |
TRY IT 1
Multiply: ![]() .
.
Show answer
![]()
When multiplying a fraction by an integer, it may be helpful to write the integer as a fraction. Any integer, a, can be written as ![]() . So, for example,
. So, for example, ![]() .
.
EXAMPLE 2
Multiply: ![]() .
.
Determine the sign of the product. The signs are the same, so the product is positive.
| Write |
|
| Multiply. | |
| Rewrite 20 to show the common factor 5 and divide it out. |  |
| Simplify. |
TRY IT 2
Multiply: ![]() .
.
Show answer
![]()
Divide Fractions
Now that we know how to multiply fractions, we are almost ready to divide. Before we can do that, that we need some vocabulary.
The reciprocal of a fraction is found by inverting the fraction, placing the numerator in the denominator and the denominator in the numerator. The reciprocal of ![]() is
is ![]() .
.
Notice that ![]() . A number and its reciprocal multiply to 1.
. A number and its reciprocal multiply to 1.
To get a product of positive 1 when multiplying two numbers, the numbers must have the same sign. So reciprocals must have the same sign.
The reciprocal of ![]() is
is ![]() , since
, since ![]() .
.
Reciprocal
The reciprocal of ![]() is
is ![]() .
.
A number and its reciprocal multiply to one ![]() .
.
To divide fractions, we multiply the first fraction by the reciprocal of the second.
Fraction Division
If ![]() are numbers where
are numbers where ![]() , then
, then
![]()
We need to say ![]() to be sure we don’t divide by zero!
to be sure we don’t divide by zero!
EXAMPLE 3
Find the quotient: ![]() .
.
| To divide, multiply the first fraction by the reciprocal of the second. | |
| Determine the sign of the product, and then multiply.. | |
| Rewrite showing common factors. |  |
| Remove common factors. | |
| Simplify. |
TRY IT 3
Find the quotient: ![]() .
.
Show answer
![]()
There are several ways to remember which steps to take to multiply or divide fractions. One way is to repeat the call outs to yourself. If you do this each time you do an exercise, you will have the steps memorized.
- “To multiply fractions, multiply the numerators and multiply the denominators.”
- “To divide fractions, multiply the first fraction by the reciprocal of the second.”
Another way is to keep two examples in mind:
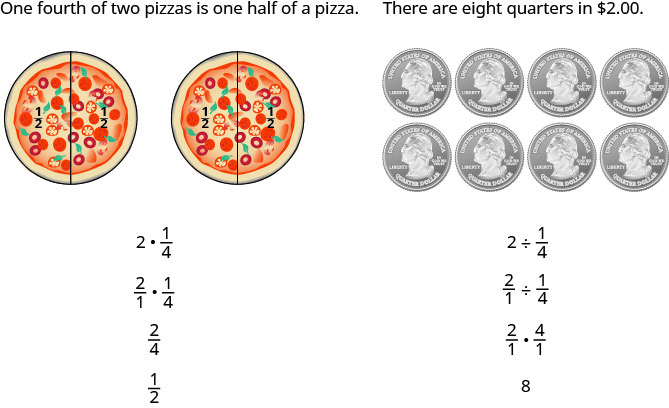
The numerators or denominators of some fractions contain fractions themselves. A fraction in which the numerator or the denominator is a fraction is called a complex fraction.
Complex Fraction
A complex fraction is a fraction in which the numerator or the denominator contains a fraction.
Some examples of complex fractions are:
![]()
To simplify a complex fraction, we remember that the fraction bar means division. For example, the complex fraction ![]() means
means ![]() .
.
EXAMPLE 4
Simplify: ![]() .
.
| Rewrite as division. | |
| Multiply the first fraction by the reciprocal of the second. | |
| Multiply. | |
| Look for common factors. |  |
| Divide out common factors and simplify. |
TRY IT 4
Simplify: ![]() .
.
Show answer
![]()
Simplify Expressions with a Fraction Bar
The line that separates the numerator from the denominator in a fraction is called a fraction bar. A fraction bar acts as grouping symbol. The order of operations then tells us to simplify the numerator and then the denominator. Then we divide.
To simplify the expression ![]() , we first simplify the numerator and the denominator separately. Then we divide.
, we first simplify the numerator and the denominator separately. Then we divide.
HOW TO: Simplify an Expression with a Fraction Bar
- Simplify the expression in the numerator. Simplify the expression in the denominator.
- Simplify the fraction.
EXAMPLE 5
Simplify: ![]() .
.
| Use the order of operations to simpliy the numerator and the denominator. | |
| Simplify the numerator and the denominator. | |
| Simplify. A negative divided by a positive is negative. |
TRY IT 5
Simplify: ![]() .
.
Show answer
![]()
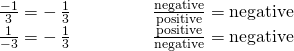
Placement of Negative Sign in a Fraction
For any positive numbers a and b,
![]()
EXAMPLE 6
Simplify: ![]() .
.
| Multiply. | |
| Simplify. | |
| Divide. |
TRY IT 6
Simplify: ![]() .
.
Show answer
4
Add or Subtract Fractions with a Common Denominator
When we multiplied fractions, we just multiplied the numerators and multiplied the denominators right straight across. To add or subtract fractions, they must have a common denominator.
Fraction Addition and Subtraction
If ![]() are numbers where
are numbers where ![]() , then
, then
![]()
To add or subtract fractions, add or subtract the numerators and place the result over the common denominator.
EXAMPLE 7
Find the sum: ![]() .
.
| Add the numerators and place the sum over the common denominator.
Simplify. |
|
TRY IT 7
Find the sum: ![]() .
.
Show answer
![]()
EXAMPLE 8
Find the difference: ![]() .
.
| Subtract the numerators and place the difference over the common denominator. | |
| Simplify. | |
| Simplify. Remember, |
TRY IT 8
Find the difference: ![]() .
.
Show answer
![]()
Now we will do an example that has both addition and subtraction.
EXAMPLE 9
Simplify: ![]() .
.
| Add and subtract fractions—do they have a common denominator? Yes. | |
| Add and subtract the numerators and place the difference over the common denominator. | |
| Simplify left to right. | |
| Simplify. |
TRY IT 9
Simplify: ![]() .
.
Show answer
![]()
Add or Subtract Fractions with Different Denominators
As we have seen, to add or subtract fractions, their denominators must be the same. The least common denominator (LCD) of two fractions is the smallest number that can be used as a common denominator of the fractions. The LCD of the two fractions is the least common multiple (LCM) of their denominators.
Least Common Denominator
The least common denominator (LCD) of two fractions is the least common multiple (LCM) of their denominators.
After we find the least common denominator of two fractions, we convert the fractions to equivalent fractions with the LCD. Putting these steps together allows us to add and subtract fractions because their denominators will be the same!
EXAMPLE 10
Add: ![]() .
.



TRY IT 10
Add: ![]() .
.
Show answer
![]()
HOW TO: Add or Subtract Fractions
- Do they have a common denominator?
- Yes—go to step 2.
- No—rewrite each fraction with the LCD (least common denominator). Find the LCD. Change each fraction into an equivalent fraction with the LCD as its denominator.
- Add or subtract the fractions.
- Simplify, if possible.
When finding the equivalent fractions needed to create the common denominators, there is a quick way to find the number we need to multiply both the numerator and denominator. This method works if we found the LCD by factoring into primes.
Look at the factors of the LCD and then at each column above those factors. The “missing” factors of each denominator are the numbers we need.

In (Example 10), the LCD, 36, has two factors of 2 and two factors of ![]() .
.
The numerator 12 has two factors of 2 but only one of 3—so it is “missing” one 3—we multiply the numerator and denominator by 3
The numerator 18 is missing one factor of 2—so we multiply the numerator and denominator by 2
We will apply this method as we subtract the fractions in the next example.
EXAMPLE 11
Subtract: ![]() .
.
Do the fractions have a common denominator? No, so we need to find the LCD.
Find the LCD.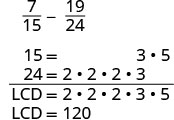 |
|
| Notice, 15 is “missing” three factors of 2 and 24 is “missing” the 5 from the factors of the LCD. So we multiply 8 in the first fraction and 5 in the second fraction to get the LCD. | |
| Rewrite as equivalent fractions with the LCD. |  |
| Simplify. | 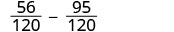 |
| Subtract. | |
| Check to see if the answer can be simplified. | |
| Both 39 and 120 have a factor of 3. | |
| Simplify. |
Do not simplify the equivalent fractions! If you do, you’ll get back to the original fractions and lose the common denominator!
TRY IT 11
Subtract: ![]() .
.
Show answer
![]()
We now have all four operations for fractions. The table below summarizes fraction operations.
| Fraction Operation | Sample Equation | What to Do |
|---|---|---|
| Fraction multiplication | Multiply the numerators and multiply the denominators | |
| Fraction division | Multiply the first fraction by the reciprocal of the second. | |
| Fraction addition | Add the numerators and place the sum over the common denominator. | |
| Fraction subtraction | Subtract the numerators and place the difference over the common denominator. |
To multiply or divide fractions, an LCD is NOT needed. To add or subtract fractions, an LCD is needed.
Use the Order of Operations to Simplify Complex Fractions
We have seen that a complex fraction is a fraction in which the numerator or denominator contains a fraction. The fraction bar indicates division. We simplified the complex fraction ![]() by dividing
by dividing ![]() by
by ![]() .
.
Now we’ll look at complex fractions where the numerator or denominator contains an expression that can be simplified. So we first must completely simplify the numerator and denominator separately using the order of operations. Then we divide the numerator by the denominator.
EXAMPLE 12
Simplify: ![]() .
.



TRY IT 12
Simplify: ![]() .
.
Show answer
![]()
HOW TO: Simplify Complex Fractions
- Simplify the numerator.
- Simplify the denominator.
- Divide the numerator by the denominator. Simplify if possible.
EXAMPLE 13
Simplify: ![]() .
.
It may help to put parentheses around the numerator and the denominator.
| Simplify the numerator (LCD = 6) and simplify the denominator (LCD = 12). | |
| Simplify. | |
| Divide the numerator by the denominator. | |
| Simplify. | |
| Divide out common factors. | |
| Simplify. |
TRY IT 13
Simplify: ![]() .
.
Show answer
2
Key Concepts
- Fraction Division: If
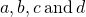 are numbers where
are numbers where 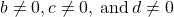 , then
, then 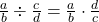 . To divide fractions, multiply the first fraction by the reciprocal of the second.
. To divide fractions, multiply the first fraction by the reciprocal of the second. - Fraction Multiplication: If
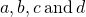 are numbers where
are numbers where 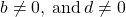 , then
, then 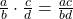 . To multiply fractions, multiply the numerators and multiply the denominators.
. To multiply fractions, multiply the numerators and multiply the denominators. - Placement of Negative Sign in a Fraction: For any positive numbers
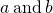 ,
, 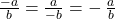 .
. - Fraction Addition and Subtraction: If
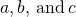 are numbers where
are numbers where 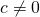 , then
, then
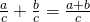 and
and 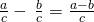 .
.
To add or subtract fractions, add or subtract the numerators and place the result over the common denominator. - Strategy for Adding or Subtracting Fractions
- Do they have a common denominator?
Yes—go to step 2.
No—Rewrite each fraction with the LCD (Least Common Denominator). Find the LCD. Change each fraction into an equivalent fraction with the LCD as its denominator. - Add or subtract the fractions.
- Simplify, if possible. To multiply or divide fractions, an LCD IS NOT needed. To add or subtract fractions, an LCD IS needed.
- Do they have a common denominator?
- Simplify Complex Fractions
- Simplify the numerator.
- Simplify the denominator.
- Divide the numerator by the denominator. Simplify if possible.
Glossary
- least common denominator
- The least common denominator (LCD) of two fractions is the Least common multiple (LCM) of their denominators.
1.3 Exercise Set
In the following exercises, multiply.
In the following exercises, divide.
In the following exercises, simplify.
In the following exercises, add.
In the following exercises, add or subtract.
In the following exercises, simplify.
- Decorating. Kayla is making covers for the throw pillows on her sofa. For each pillow cover, she needs
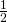 yard of print fabric and
yard of print fabric and 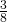 yard of solid fabric. What is the total amount of fabric Kayla needs for each pillow cover?
yard of solid fabric. What is the total amount of fabric Kayla needs for each pillow cover? - Baking. A recipe for chocolate chip cookies calls for
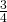 cup brown sugar. Leona wants to double the recipe. a) How much brown sugar will Leona need? Show your calculation. b) Measuring cups usually come in sets of
cup brown sugar. Leona wants to double the recipe. a) How much brown sugar will Leona need? Show your calculation. b) Measuring cups usually come in sets of 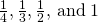 cup. Draw a diagram to show two different ways that Leona could measure the brown sugar needed to double the cookie recipe.
cup. Draw a diagram to show two different ways that Leona could measure the brown sugar needed to double the cookie recipe. - Portions. Regin purchased a bulk package of candy that weighs
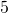 pounds. He wants to sell the candy in little bags that hold
pounds. He wants to sell the candy in little bags that hold 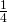 pound. How many little bags of candy can he fill from the bulk package?
pound. How many little bags of candy can he fill from the bulk package?
Answers:
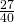
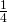
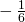
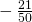
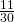
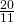
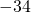
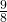
 .
.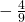
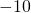
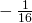
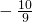
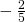
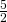
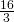
- 0
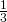
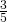
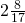
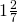
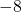
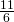
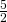
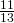
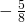
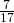
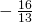
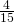
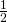
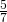
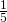
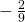
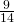

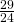
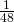
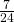
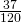
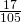
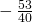
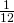
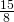
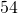
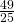
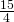
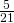
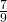
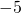
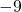
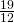
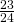
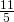
- 1
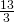
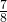 yard
yard- a)
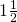 cups b) answers will vary
cups b) answers will vary - 20 bags
Attributions
This chapter has been adapted from “Add and Subtract Fractions” in Elementary Algebra (OpenStax) by Lynn Marecek and MaryAnne Anthony-Smith, which is under a CC BY 4.0 Licence. Adapted by Izabela Mazur. See the Copyright page for more information.

