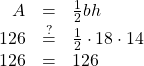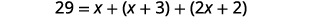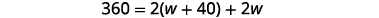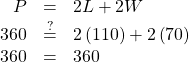2. Solving Linear Equations and Inequalities
2.4 Solve a Formula for a Specific Variable
Learning Objectives
By the end of this section it is expected that you will be able to:
- Solve a formula for a specific variable
- Use formulas to solve applications
Solve a Formula for Specific Variable
In the last section we have worked with some geometry formulas when solving problems. A formula is a mathematical description of the relationship between variables. Formulas are also used in the sciences, such as chemistry, physics, and biology. In medicine they are used for calculations for dispensing medicine or determining body mass index. Spreadsheet programs rely on formulas to make calculations. It is important to be familiar with formulas and be able to manipulate them easily.
To solve a formula for a specific variable means to isolate that variable on one side of the equals sign with a coefficient of 1. All other variables and constants are on the other side of the equals sign. To see how to solve a formula for a specific variable, we will start with the distance, rate and time formula.
EXAMPLE 1
Solve the formula ![]() for
for ![]() :
:
- when
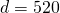 and
and 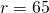
- in general
We will write the solutions side-by-side to demonstrate that solving a formula in general uses the same steps as when we have numbers to substitute.
| a) when |
b) in general | ||||
| Write the formula. | Write the formula. | ||||
| Substitute. | |||||
| Divide, to isolate |
Divide, to isolate |
||||
| Simplify. | Simplify. | ||||
We say the formula ![]() is solved for
is solved for ![]() .
.
TRY IT 1
Solve the formula ![]() for
for ![]() :
:
a) when ![]() b) in general
b) in general
Show answer
a) ![]() b)
b) ![]()
EXAMPLE 2
Solve the formula ![]() for
for ![]() :
:
a) when ![]() and
and ![]() b) in general
b) in general
| a) when |
b) in general | ||||
| Write the formula. | 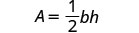 |
Write the formula. | 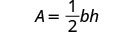 |
||
| Substitute. | 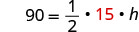 |
||||
| Clear the fractions. | 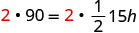 |
Clear the fractions. | 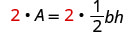 |
||
| Simplify. | 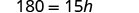 |
Simplify. | 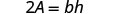 |
||
| Solve for |
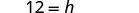 |
Solve for |
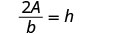 |
||
We can now find the height of a triangle, if we know the area and the base, by using the formula ![]() .
.
TRY IT 2
Use the formula ![]() to solve for
to solve for ![]() :
:
a) when ![]() and
and ![]() b) in general
b) in general
Show answer
a) ![]() b)
b) ![]()
The formula ![]() is used to calculate simple interest, I, for a principal, P, invested at rate, r, for t years.
is used to calculate simple interest, I, for a principal, P, invested at rate, r, for t years.
EXAMPLE 3
Solve the formula ![]() to find the principal,
to find the principal, ![]() :
:
a) when ![]() ,
, ![]() ,
, ![]() b) in general
b) in general
| a) |
b) in general | ||
| Write the formula. | 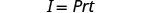 |
Write the formula. | 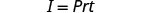 |
| Substitute. | 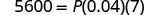 |
||
| Simplify. | 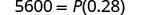 |
Simplify. | 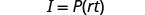 |
| Divide, to isolate P. | 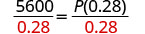 |
Divide, to isolate P. | 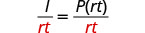 |
| Simplify. | 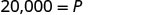 |
Simplify. | 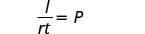 |
| The principal is | 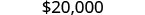 |
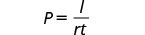 |
|
TRY IT 3
Use the formula ![]() to find the principal,
to find the principal, ![]() :
:
a) when ![]() ,
, ![]() ,
, ![]() b) in general
b) in general
Show answer
a) $12,000 b) ![]()
Later in this class, and in future algebra classes, you’ll encounter equations that relate two variables, usually x and y. You might be given an equation that is solved for y and need to solve it for x, or vice versa. In the following example, we’re given an equation with both x and y on the same side and we’ll solve it for y.
EXAMPLE 4
Solve the formula ![]() for y:
for y:
a) when ![]() b) in general
b) in general
| a) when |
b) in general | ||
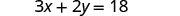 |
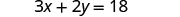 |
||
| Substitute. | 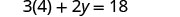 |
||
| Subtract to isolate the |
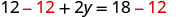 |
Subtract to isolate the |
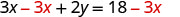 |
| Divide. | 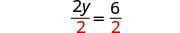 |
Divide. | 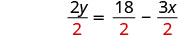 |
| Simplify. | 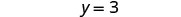 |
Simplify. | 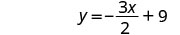 |
TRY IT 4
Solve the formula ![]() for y:
for y:
a) when ![]() b) in general
b) in general
Show answer
a) ![]() b)
b) ![]()
Now we will solve a formula in general without using numbers as a guide.
EXAMPLE 5
Solve the formula ![]() for
for ![]() .
.
| We will isolate |
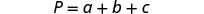 |
| Both |
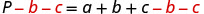 |
| Simplify. |  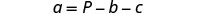 |
TRY IT 5
Solve the formula ![]() for b.
for b.
Show answer
![]()
EXAMPLE 6
Solve the formula ![]() for y.
for y.
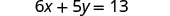 |
|
| Subtract |
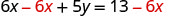 |
| Simplify. | 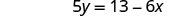 |
| Divide by 5 to make the coefficient 1. | 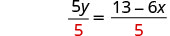 |
| Simplify. | 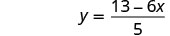 |
The fraction is simplified. We cannot divide ![]() by 5
by 5
TRY IT 6
Solve the formula ![]() for y.
for y.
Show answer
![]()
Geometric formulas often need to be solved for another variable, too. The formula ![]() is used to find the volume of a right circular cone when given the radius of the base and height. In the next example, we will solve this formula for the height.
is used to find the volume of a right circular cone when given the radius of the base and height. In the next example, we will solve this formula for the height.
EXAMPLE 7
Solve the formula ![]() for h.
for h.
| Write the formula. | 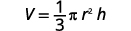 |
| Remove the fraction on the right. | 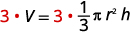 |
| Simplify. | 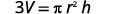 |
| Divide both sides by |
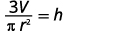 |
We could now use this formula to find the height of a right circular cone when we know the volume and the radius of the base, by using the formula ![]()
TRY IT 7
Use the formula ![]() to solve for b.
to solve for b.
Show answer
![]()
In the sciences, we often need to change temperature from Fahrenheit to Celsius or vice versa. If you travel in a foreign country, you may want to change the Celsius temperature to the more familiar Fahrenheit temperature.
EXAMPLE 8
Solve the formula ![]() for F.
for F.
| Write the formula. | 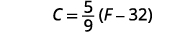 |
| Remove the fraction on the right. | 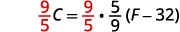 |
| Simplify. | 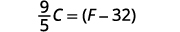 |
| Add 32 to both sides. | 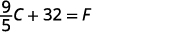 |
We can now use the formula ![]() to find the Fahrenheit temperature when we know the Celsius temperature.
to find the Fahrenheit temperature when we know the Celsius temperature.
TRY IT 8
Solve the formula ![]() for C.
for C.
Show answer
![]()
Use Formulas to Solve Applications
One formula you will use often in algebra and in everyday life is the formula for distance traveled by an object moving at a constant rate. Rate is an equivalent word for “speed.” The basic idea of rate may already familiar to you. Do you know what distance you travel if you drive at a steady rate of 60 miles per hour for 2 hours? (This might happen if you use your car’s cruise control while driving on the highway.) If you said 120 miles, you already know how to use this formula!
Distance, Rate, and Time
For an object moving at a uniform (constant) rate, the distance traveled, the elapsed time, and the rate are related by the formula:
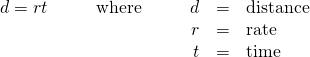
We will use the Strategy for Solving Applications that we used earlier in this chapter. When our problem requires a formula, we change Step 4. In place of writing a sentence, we write the appropriate formula. We write the revised steps here for reference.
HOW TO: Solve an application (with a formula).
- Read the problem. Make sure all the words and ideas are understood.
- Identify what we are looking for.
- Name what we are looking for. Choose a variable to represent that quantity.
- Translate into an equation. Write the appropriate formula for the situation. Substitute in the given information.
- Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
You may want to create a mini-chart to summarize the information in the problem. See the chart in this first example.
EXAMPLE 9
Adam rides his bike at a uniform rate of 12 miles per hour for ![]() hours. What distance has he traveled?
hours. What distance has he traveled?
| Step 1. Read the problem. | ||
| Step 2. Identify what you are looking for. | distance traveled | |
| Step 3. Name. Choose a variable to represent it. | Let d = distance. | |
| Step 4. Translate: Write the appropriate formula. | ||
 |
||
| Substitute in the given information. | ||
| Step 5. Solve the equation. | ||
| Step 6. Check | ||
| Does 42 miles make sense? | ||
| Jamal rides: | ||
 |
||
| Step 7. Answer the question with a complete sentence. | Jamal rode 42 miles. | |
TRY IT 9
Lindsay drove for ![]() hours at 60 miles per hour. How much distance did she travel?
hours at 60 miles per hour. How much distance did she travel?
Show answer
330 miles
EXAMPLE 10
Rey is planning to drive from his house in Saskatoon to visit his grandmother in Winnipeg, a distance of 520 miles. If he can drive at a steady rate of 65 miles per hour, how many hours will the trip take?
| Step 1. Read the problem. | |
| Step 2. Identify what you are looking for. | How many hours (time) |
| Step 3. Name. Choose a variable to represent it. |
Let t = time. |
 |
|
| Step 4. Translate. Write the appropriate formula. |
|
| Substitute in the given information. | |
| Step 5. Solve the equation. | |
| Step 6. Check. Substitute the numbers into the formula and make sure the result is a true statement. |
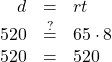 |
| Step 7. Answer the question with a complete sentence. Rey’s trip will take 8 hours. |
TRY IT 10
Lee wants to drive from Kamloops to his brother’s apartment in Banff, a distance of 495 km. If he drives at a steady rate of 90 km/h, how many hours will the trip take?
Show answer
5 1/2 hours
When we solve geometry applications, we adapt our problem solving strategy, use some common geometry formulas, and draw a figure and label it with given information.
The next example involves the area of a triangle. The area of a triangle is one-half the base times the height. We can write this as ![]() where b = length of the base and h = height.
where b = length of the base and h = height.
EXAMPLE 11
The area of a triangular painting is 126 square inches. The base is 18 inches. What is the height?
Solution
| Step 1. Read the problem. | |
| Step 2. Identify what you are looking for. | height of a triangle |
| Step 3. Name. | |
| Choose a variable to represent it. | Let |
| Draw the figure and label it with the given information. | Area = 126 sq. in. |
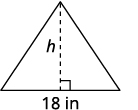 |
|
| Step 4. Translate. | |
| Write the appropriate formula. | |
| Substitute in the given information. | |
| Step 5. Solve the equation. | |
| Divide both sides by 9. | |
| Step 6. Check.
|
|
| Step 7. Answer the question. | The height of the triangle is 14 inches. |
TRY IT 11
The area of a triangular church window is 90 square metres. The base of the window is 15 metres. What is the window’s height?
Show answer
The window’s height is 12 metres.
The next example is about the perimeter of a triangle. Since the perimeter is just the distance around the triangle, we find the sum of the lengths of its three sides. We can write this as ![]() where a, b, and c are the lengths of the sides.
where a, b, and c are the lengths of the sides.
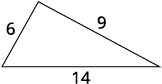
EXAMPLE 12
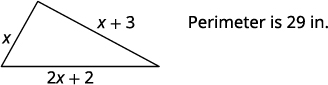
One side of a triangle is three inches more than the first side. The third side is two inches more than twice the first. The perimeter is 29 inches. Find the length of the three sides of the triangle.
| Step 1. Read the problem. | |
| Step 2. Identify what we are looking for. | the lengths of the three sides of a triangle |
| Step 3. Name. Choose a variable to
represent the length of the first side. |
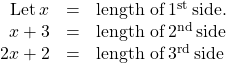
|
| Step 4. Translate.
Write the appropriate formula. Substitute in the given information. |
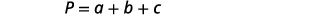
|
| Step 5. Solve the equation. |  |
| Step 6. Check.
|
|
| Step 7. Answer the question. | The lengths of the sides of the triangle
are 6, 9, and 14 inches. |
TRY IT 12
One side of a triangle is seven inches more than the first side. The third side is four inches less than three times the first. The perimeter is 28 inches. Find the length of the three sides of the triangle.
Show answer
The lengths of the sides of the triangle are 5, 11 and 12 inches.
EXAMPLE 13
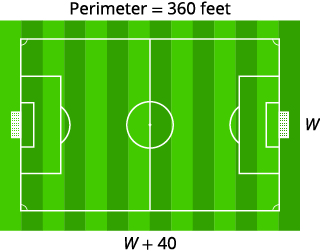
The perimeter of a rectangular soccer field is 360 feet. The length is 40 feet more than the width. Find the length and width.
Solution
| Step 1. Read the problem. | |
| Step 2. Identify what we are looking for. | the length and width of the soccer field |
| Step 3. Name. Choose a variable to represent it.
The length is 40 feet more than the width. Draw the figure and label it with the given information. |
Let w = width.
|
| Step 4. Translate.
Write the appropriate formula and substitute. |
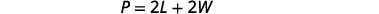
|
| Step 5. Solve the equation. |  |
| Step 6. Check.
|
|
| Step 7. Answer the question. | The length of the soccer field is 110 feet
and the width is 70 feet. |
TRY IT 13
The perimeter of a rectangular swimming pool is 200 feet. The length is 40 feet more than the width. Find the length and width.
Show answer
The length of the swimming pool is 70 feet and the width is 30 feet.
Key Concepts
- To solve a formula for a specific variable means to get that variable by itself with a coefficient of 1 on one side of the equation and all other variables and constants on the other side.
- To Solve an Application (with a formula)
- Read the problem. Make sure all the words and ideas are understood.
- Identify what we are looking for.
- Name what we are looking for. Choose a variable to represent that quantity.
- Translate into an equation. Write the appropriate formula for the situation. Substitute in the given information.
- Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
- Distance, Rate and Time
For an object moving at a uniform (constant) rate, the distance traveled, the elapsed time, and the rate are related by the formula: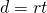 where d = distance, r = rate, t = time.
where d = distance, r = rate, t = time.
2.4 Exercise Set
In the following exercises, use the formula ![]() .
.
- Solve for
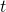
- when

- in general
- when
- Solve for

- when
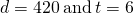
- in general
- when
In the following exercises, solve the formula .
- Solve the formula
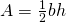 for
for 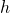
- when
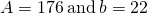
- in general
- when
- Solve the formula I=Prt for the principal, P for
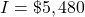 ,
,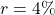 ,
,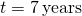
- in general
- Solve for the time, t for
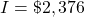 ,
, 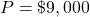 ,
, 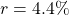
- in general
- Solve the formula
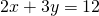 for y
for y
- when
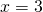
- in general
- when
- Solve the formula
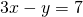 for y
for y
- when
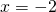
- in general
- when
- Solve
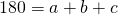 for
for  .
. - Solve the formula
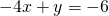 for y.
for y. - Solve the formula
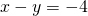 for y.
for y. - Solve the formula
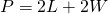 for
for 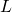 .
. - Solve the formula
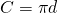 for
for 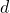 .
. - Solve the formula
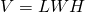 for
for 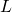 .
. - Solve the formula
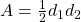 for
for 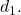
- Solve the formula
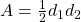 for
for 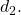
- Solve the formula
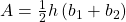 for
for 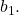
- Solve the formula
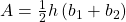 for
for 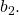
- Solve the formula
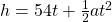 for a.
for a. - Solve the formula
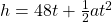 for a.
for a.
In the following exercises, solve using a geometry formula.
- A triangular flag has area 0.75 square feet and height 1.5 foot. What is its base?
- What is the base of triangular window with area 207 square inches and height 18 inches?
- The width of a rectangle is seven metres less than the length. The perimeter is 58 metres. Find the length and width.
- The width of the rectangle is 0.7 metres less than the length. The perimeter of a rectangle is 52.6 metres. Find the dimensions of the rectangle.
- The perimeter of a rectangle of 150 feet. The length of the rectangle is twice the width. Find the length and width of the rectangle.
- The length of the rectangle is three metres less than twice the width. The perimeter of a rectangle is 36 metres. Find the dimensions of the rectangle.
- The perimeter of a triangle is 39 feet. One side of the triangle is one foot longer than the second side. The third side is two feet longer than the second side. Find the length of each side.
- One side of a triangle is twice the smallest side. The third side is five feet more than the shortest side. The perimeter is 17 feet. Find the lengths of all three sides.
- The perimeter of a rectangular field is 560 yards. The length is 40 yards more than the width. Find the length and width of the field.
- A rectangular parking lot has perimeter 250 feet. The length is five feet more than twice the width. Find the length and width of the parking lot.
In the following exercises, solve.
- Socorro drove for
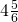 hours at 60 miles per hour. How much distance did she travel?
hours at 60 miles per hour. How much distance did she travel? - Francie rode her bike for
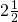 hours at 12 miles per hour. How far did she ride?
hours at 12 miles per hour. How far did she ride? - Marta is taking the bus from Abbotsford to Cranbrook. The distance is 774 km and the bus travels at a steady rate of 86 miles per hour. How long will the bus ride be?
- Halle wants to ride his bike from Golden, BC to Banff, AB. The distance is 140 km. If he rides at a steady rate of 20 km/h, how many hours will the trip take?
- Alejandra is driving to Prince George, 450 km away. If she wants to be there in 6 hours, at what rate does she need to drive?
- Philip got a ride with a friend from Calgary to Kelowna, a distance of 890 km. If the trip took 10 hours, how fast was the friend driving?
- Converting temperature. Yon was visiting the United States and he saw that the temperature in Seattle one day was 50o Fahrenheit. Solve for C in the formula
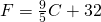 to find the Celsius temperature.
to find the Celsius temperature.
Answers
-
-
-
-
-
-
-
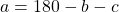
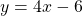
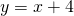
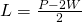
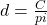
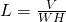
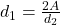
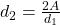
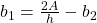
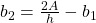
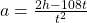
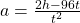
- 1 foot
- 23 inches
- 18 metres, 11 metres
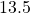 m,
m, 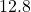 m
m- 25 ft, 50 ft
- 7 m, 11 m
- 12 ft, 13 ft, 14 ft
- 3 ft, 6 ft, 8 ft
- 120 yd, 160 yd
- 40 ft, 85 ft
- 290 miles
- 30 miles
- 9 hours.
- 7 hours
- 75 km/h
- 89 km/h
- 10°C