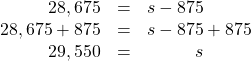2. Solving Linear Equations and Inequalities
2.3 Use a Problem Solving Strategy
Learning Objectives
By the end of this section it is expected that you will be able to:
- Translate to an equation and solve
- Translate and solve applications
Translate to an Equation and Solve
To solve applications algebraically, we will begin by translating from English sentences into equations. Our first step is to look for the word (or words) that would translate to the equals sign. In the next few examples, we will translate sentences into equations and then solve the equations.
EXAMPLE 1
Translate and solve: Eleven more than x is equal to 54.
| Translate. | 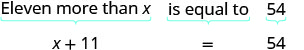 |
| Subtract 11 from both sides. |  |
| Simplify. |  |
| Check: Is 54 eleven more than 43? |
TRY IT 1
Translate and solve: Ten more than x is equal to 41.
Show answer
![]()
EXAMPLE 2
Translate and solve: The number 143 is the product of ![]() and y.
and y.
Begin by translating the sentence into an equation.
| Translate. |  |
| Divide by |
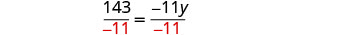 |
| Simplify. |  |
| Check: | 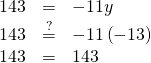 |
TRY IT 2
Translate and solve: The number 132 is the product of −12 and y.
Show answer
![]()
EXAMPLE 3
Translate and solve: The quotient of ![]() and
and ![]() is
is ![]() .
.
Begin by translating the sentence into an equation.
| Translate. | 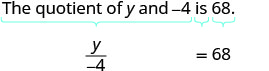 |
| Multiply both sides by |
 |
| Simplify. |  |
| Check: | Is the quotient of |
| Let |
Is the quotient of |
| Translate. | |
| Simplify. |
TRY IT 3
Translate and solve: The quotient of ![]() and
and ![]() is 72.
is 72.
Show answer
![]()
EXAMPLE 4
Translate and solve: Three-fourths of ![]() is 18.
is 18.
Begin by translating the sentence into an equation. Remember, “of” translates into multiplication.
| Translate. | 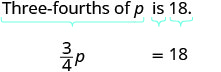 |
| Multiply both sides by |
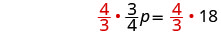 |
| Simplify. |  |
| Check: | Is three-fourths of p equal to 18? |
| Let |
Is three-fourths of 24 equal to 18? |
| Translate. | |
| Simplify. |
TRY IT 4
Translate and solve: Two-fifths of ![]() is 16.
is 16.
Show answer
![]()
Translate and Solve Applications
Most of the time a question that requires an algebraic solution comes out of a real life situation. To begin, that question is asked in English (or the language of the person asking) and not in math symbols. Because of this, it is an important skill to be able to translate an everyday situation into algebraic language.
We will start by restating the problem in just one sentence, assign a variable, and then translate the sentence into an equation to solve. When assigning a variable, choose a letter that reminds you of what you are looking for. For example, you might use q for the number of quarters if you were solving a problem about coins.
EXAMPLE 5
The Alec family recycled newspapers for two months. The two months of newspapers weighed a total of 57 pounds. The second month, the newspapers weighed 28 pounds. How much did the newspapers weigh the first month?







TRY IT 5
Translate into an algebraic equation and solve:
The Snider family has two cats, Zeus and Athena. Together, they weigh 23 pounds. Zeus weighs 16 pounds. How much does Athena weigh?
Show answer
7 pounds
HOW TO: Solve an application
- Read the problem. Make sure all the words and ideas are understood.
- Identify what we are looking for.
- Name what we are looking for. Choose a variable to represent that quantity.
- Translate into an equation. It may be helpful to restate the problem in one sentence with the important information.
- Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
EXAMPLE 6
Abdullah paid $28,675 for his new car. This was $875 less than the sticker price. What was the sticker price of the car?
| Step 1. Read the problem. | |
| Step 2. Identify what we are looking for. | “What was the sticker price of the car?” |
| Step 3. Name what we are looking for. Choose a variable to represent that quantity. |
Let |
| Step 4. Translate into an equation. Restate the problem in one sentence. | $28,675 is $875 less than the sticker price |
| Step 5. Solve the equation. | $28,675 is $875 less than s
|
| Step 6. Check the answer. | Is $875 less than $29,550 equal to $28,675? |
| Step 7. Answer the question with a complete sentence. | The sticker price of the car was $29,550. |
TRY IT 6
Translate into an algebraic equation and solve:
Jaffrey paid $19,875 for her new car. This was $1,025 less than the sticker price. What was the sticker price of the car?
Show answer
$20,900
Now that we have a problem solving strategy, we will use it on several different types of word problems. The first type we will work on is “number problems”.
EXAMPLE 7
The sum of twice a number and seven is 15. Find the number.
| Step 1. Read the problem. | |
| Step 2. Identify what we are looking for. | the number |
| Step 3. Name. Choose a variable to represent the number. | Let |
| Step 4. Translate. | |
| Restate the problem as one sentence. |  |
| Translate into an equation. |  |
| Step 5. Solve the equation. |  |
| Subtract 7 from each side and simplify. |  |
| Divide each side by 2 and simplify. |  |
| Step 6. Check. | |
| Is the sum of twice 4 and 7 equal to 15? | |
| Step 7. Answer the question. | The number is 4. |
Did you notice that we left out some of the steps as we solved this equation? If you’re not yet ready to leave out these steps, write down as many as you need.
TRY IT 7
The sum of four times a number and two is 14. Find the number.
Show answer
3
Some number word problems ask us to find two or more numbers. It may be tempting to name them all with different variables, but so far we have only solved equations with one variable. In order to avoid using more than one variable, we will define the numbers in terms of the same variable. Be sure to read the problem carefully to discover how all the numbers relate to each other.
EXAMPLE 8
One number is five more than another. The sum of the numbers is 21. Find the numbers.
| Step 1. Read the problem. | |
| Step 2. Identify what we are looking for. | We are looking for two numbers. |
| Step 3. Name. We have two numbers to name and need a name for each. | |
| Choose a variable to represent the first number. | Let |
| What do we know about the second number? | One number is five more than another. |
| Step 4. Translate. Restate the problem as one sentence with all the important information. | The sum of the 1st number and the 2nd number is 21. |
| Translate into an equation. | 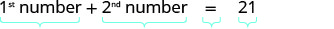 |
| Substitute the variable expressions. | 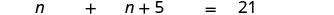 |
| Step 5. Solve the equation. | 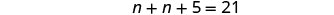 |
| Combine like terms. | 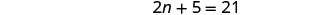 |
| Subtract 5 from both sides and simplify. |  |
| Divide by 2 and simplify. |  |
| Find the second number, too. |  |
 |
|
 |
|
| Step 6. Check. | |
| Do these numbers check in the problem? | |
| Is one number 5 more than the other? | |
| Is thirteen 5 more than 8? Yes. | |
| Is the sum of the two numbers 21? | |
| Step 7. Answer the question. | The numbers are 8 and 13. |
TRY IT 8
One number is six more than another. The sum of the numbers is twenty-four. Find the numbers.
Show answer
9, 15
Now, we will use the problem solving strategy to solve some geometry problems.
EXAMPLE 9
The length of a rectangle is ![]() metres and the width is
metres and the width is ![]() metres. Find a) the perimeter, and b) the area.
metres. Find a) the perimeter, and b) the area.
| a) | |
| Step 1. Read the problem. Draw the figure and label it with the given information. | 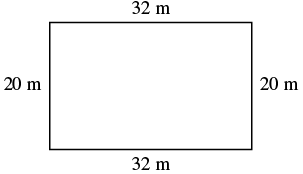 |
| Step 2. Identify what you are looking for. | the perimeter of a rectangle |
| Step 3. Name. Choose a variable to represent it. | Let P = the perimeter |
| Step 4. Translate. Write the appropriate formula. Substitute. |
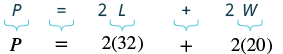 |
| Step 5. Solve the equation. | 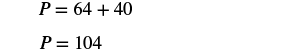 |
| Step 6. Check: | 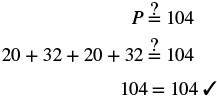 |
| Step 7. Answer the question. | The perimeter of the rectangle is 104 metres. |
| b) | |
| Step 1. Read the problem. Draw the figure and label it with the given information. | 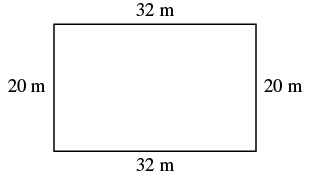 |
| Step 2. Identify what you are looking for. | the area of a rectangle |
| Step 3. Name. Choose a variable to represent it. | Let A = the area |
| Step 4. Translate. Write the appropriate formula. Substitute. |
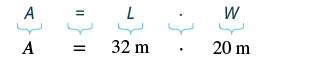 |
| Step 5. Solve the equation. |  |
| Step 6. Check: |  |
| Step 7. Answer the question. | The area of the rectangle is 60 square metres. |
TRY IT 9
The length of a rectangle is ![]() yards and the width is
yards and the width is ![]() yards. Find a) the perimeter and b) the area.
yards. Find a) the perimeter and b) the area.
Show answer
a) 340 yd
b) 6000 sq. yd
EXAMPLE 10
Find the length of a rectangle with perimeter ![]() inches and width
inches and width ![]() inches.
inches.
| Step 1. Read the problem. Draw the figure and label it with the given information. | 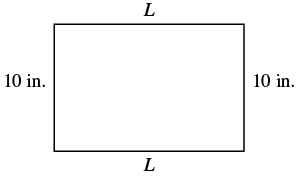 |
| Step 2. Identify what you are looking for. | the length of the rectangle |
| Step 3. Name. Choose a variable to represent it. | Let L = the length |
| Step 4. Translate. Write the appropriate formula. Substitute. |
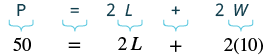 |
| Step 5. Solve the equation. | 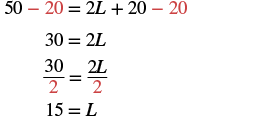 |
| Step 6. Check: | 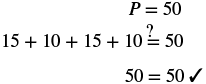 |
| Step 7. Answer the question. | The length is 15 inches. |
TRY IT 10
Find the length of a rectangle with a perimeter of ![]() inches and width of
inches and width of ![]() inches.
inches.
Show answer
15 in.
EXAMPLE 11
The area of a rectangular room is ![]() square feet. The length is
square feet. The length is ![]() feet. What is the width?
feet. What is the width?
| Step 1. Read the problem. | 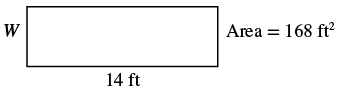 |
| Step 2. Identify what you are looking for. | the width of a rectangular room |
| Step 3. Name. Choose a variable to represent it. | Let W = width |
| Step 4.Translate. Write the appropriate formula and substitute in the given information. |
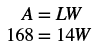 |
| Step 5. Solve the equation. | 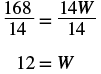 |
| Step 6. Check: | 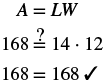 |
| Step 7. Answer the question. | The width of the room is 12 feet. |
TRY IT 11
The area of a rectangle is ![]() square feet. The length is
square feet. The length is ![]() feet. What is the width?
feet. What is the width?
Show answer
26 ft
EXAMPLE 12
The perimeter of a rectangular swimming pool is ![]() feet. The length is
feet. The length is ![]() feet more than the width. Find the length and width.
feet more than the width. Find the length and width.
| Step 1. Read the problem. Draw the figure and label it with the given information. | 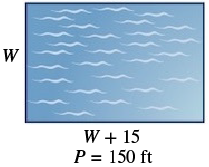 |
| Step 2. Identify what you are looking for. | the length and width of the pool |
| Step 3. Name. Choose a variable to represent it. The length is 15 feet more than the width. |
Let |
| Step 4.Translate. Write the appropriate formula and substitute. |
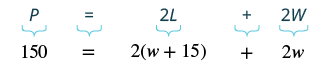 |
| Step 5. Solve the equation. | 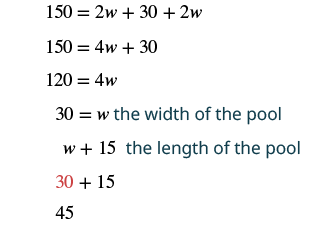 |
| Step 6. Check: | 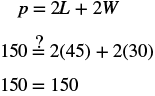 |
| Step 7. Answer the question. | The length of the pool is 45 feet and the width is 30 feet. |
TRY IT 12
The perimeter of a rectangular swimming pool is ![]() feet. The length is
feet. The length is ![]() feet more than the width. Find the length and width.
feet more than the width. Find the length and width.
Show answer
30 ft, 70 ft
The formula for the area of a triangle is ![]() , where
, where ![]() is the base and
is the base and ![]() is the height.
is the height.
To find the area of the triangle, you need to know its base and height.
EXAMPLE 13
Find the area of a triangle whose base is ![]() inches and whose height is
inches and whose height is ![]() inches.
inches.
| Step 1. Read the problem. Draw the figure and label it with the given information. | 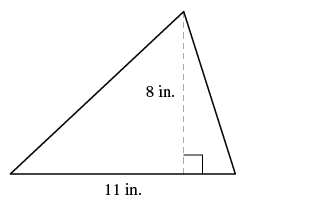 |
| Step 2. Identify what you are looking for. | the area of the triangle |
| Step 3. Name. Choose a variable to represent it. | let A = area of the triangle |
| Step 4.Translate. Write the appropriate formula. Substitute. |
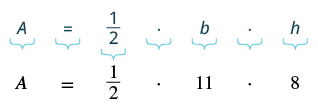 |
| Step 5. Solve the equation. | 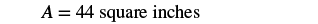 |
| Step 6. Check: | 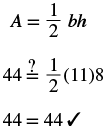 |
| Step 7. Answer the question. | The area is 44 square inches. |
TRY IT 13
Find the area of a triangle with base ![]() inches and height
inches and height ![]() inches.
inches.
Show answer
13 sq. in.
EXAMPLE 14
The perimeter of a triangular garden is ![]() feet. The lengths of two sides are
feet. The lengths of two sides are ![]() feet and
feet and ![]() feet. How long is the third side?
feet. How long is the third side?
| Step 1. Read the problem. Draw the figure and label it with the given information. | 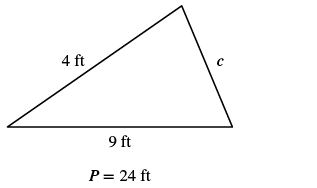 |
| Step 2. Identify what you are looking for. | length of the third side of a triangle |
| Step 3. Name. Choose a variable to represent it. | Let c = the third side |
| Step 4.Translate. Write the appropriate formula. Substitute in the given information. |
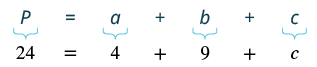 |
| Step 5. Solve the equation. |  |
| Step 6. Check: | 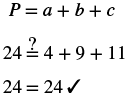 |
| Step 7. Answer the question. | The third side is 11 feet long. |
TRY IT 14
The perimeter of a triangular garden is ![]() feet. The lengths of two sides are
feet. The lengths of two sides are ![]() feet and
feet and ![]() feet. How long is the third side?
feet. How long is the third side?
Show answer
8 ft
EXAMPLE 15
The area of a triangular church window is ![]() square metres. The base of the window is
square metres. The base of the window is ![]() metres. What is the window’s height?
metres. What is the window’s height?
| Step 1. Read the problem. Draw the figure and label it with the given information. | 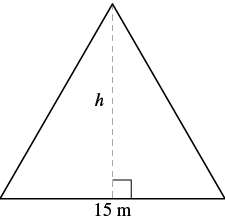 |
| Step 2. Identify what you are looking for. | height of a triangle |
| Step 3. Name. Choose a variable to represent it. | Let h = the height |
| Step 4.Translate. Write the appropriate formula. Substitute in the given information. |
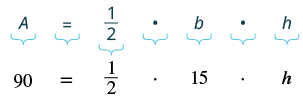 |
| Step 5. Solve the equation. |  |
| Step 6. Check: | 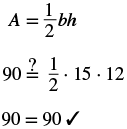 |
| Step 7. Answer the question. | The height of the triangle is 12 metres. |
TRY IT 15
The area of a triangular painting is ![]() square inches. The base is
square inches. The base is ![]() inches. What is the height?
inches. What is the height?
Show answer
14 in.
Key Concepts
- To translate a sentence to an equation
- Locate the “equals” word(s). Translate to an equal sign (=).
- Translate the words to the left of the “equals” word(s) into an algebraic expression.
- Translate the words to the right of the “equals” word(s) into an algebraic expression.
- To solve an application
- Read the problem. Make sure all the words and ideas are understood.
- Identify what we are looking for.
- Name what we are looking for. Choose a variable to represent that quantity.
- Translate into an equation. It may be helpful to restate the problem in one sentence with the important information.
- Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
2.3 Exercise Set
In the following exercises, translate to an equation and then solve it.
- Nine more than
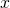 is equal to 52.
is equal to 52. - Ten less than m is
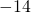 .
. - The sum of y and
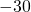 is 40.
is 40. - The difference of
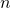 and
and 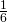 is
is 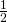 .
. - The sum of
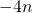 and
and 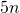 is
is 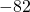 .
. - 133 is the product of
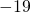 and n.
and n. - The quotient of
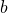 and
and 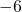 is 18.
is 18. - Three-tenths of x is 15.
- The sum of two-fifths and f is one-half.
- The difference of q and one-eighth is three-fourths
In the following exercises, translate into an equation and solve.
- Avril rode her bike a total of 18 miles, from home to the library and then to the beach. The distance from Avril’s house to the library is 7 miles. What is the distance from the library to the beach?
- Eva’s daughter is 15 years younger than her son. Eva’s son is 22 years old. How old is her daughter?
- For a family birthday dinner, Celeste bought a turkey that weighed 5 pounds less than the one she bought for Thanksgiving. The birthday turkey weighed 16 pounds. How much did the Thanksgiving turkey weigh?
- Arjun’s temperature was 0.7 degrees higher this morning than it had been last night. His temperature this morning was 101.2 degrees. What was his temperature last night?
- Ron’s paycheck this week was $17.43 less than his paycheck last week. His paycheck this week was $103.76. How much was Ron’s paycheck last week?
In the following exercises, solve each number word problem
- The sum of a number and eight is 12. Find the number.
- The difference of twice a number and seven is 17. Find the number.
- Three times the sum of a number and nine is 12. Find the number.
- One number is six more than the other. Their sum is 42. Find the numbers.
- The sum of two numbers is
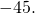 One number is nine more than the other. Find the numbers.
One number is nine more than the other. Find the numbers. - One number is 14 less than another. If their sum is increased by seven, the result is 85. Find the numbers.
- One number is one more than twice another. Their sum is
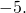 Find the numbers.
Find the numbers.
In the following exercises, find the a) perimeter and b) area of each rectangle.
- The length of a rectangle is
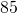 feet and the width is
feet and the width is 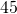 feet.
feet. - A rectangular room is
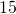 feet wide by
feet wide by 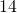 feet long.
feet long.
In the following exercises, solve.
- Find the length of a rectangle with perimeter
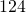 inches and width
inches and width 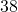 inches.
inches. - Find the width of a rectangle with perimeter
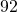 metres and length
metres and length 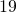 metres.
metres. - The area of a rectangle is
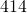 square metres. The length is
square metres. The length is 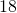 metres. What is the width?
metres. What is the width? - The length of a rectangle is
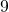 inches more than the width. The perimeter is
inches more than the width. The perimeter is 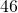 inches. Find the length and the width.
inches. Find the length and the width. - The perimeter of a rectangle is
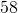 metres. The width of the rectangle is
metres. The width of the rectangle is 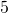 metres less than the length. Find the length and the width of the rectangle.
metres less than the length. Find the length and the width of the rectangle. - The width of the rectangle is
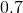 metres less than the length. The perimeter of a rectangle is
metres less than the length. The perimeter of a rectangle is 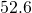 metres. Find the dimensions of the rectangle.
metres. Find the dimensions of the rectangle. - The perimeter of a rectangle is
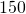 feet. The length of the rectangle is twice the width. Find the length and width of the rectangle.
feet. The length of the rectangle is twice the width. Find the length and width of the rectangle. - The length of a rectangle is
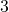 metres less than twice the width. The perimeter is
metres less than twice the width. The perimeter is 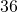 metres. Find the length and width.
metres. Find the length and width. - The width of a rectangular window is
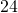 inches. The area is
inches. The area is 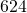 square inches. What is the length?
square inches. What is the length? - The area of a rectangular roof is
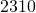 square metres. The length is
square metres. The length is 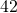 metres. What is the width?
metres. What is the width? - The perimeter of a rectangular courtyard is
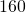 feet. The length is
feet. The length is 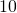 feet more than the width. Find the length and the width.
feet more than the width. Find the length and the width. - The width of a rectangular window is
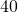 inches less than the height. The perimeter of the doorway is
inches less than the height. The perimeter of the doorway is 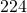 inches. Find the length and the width.
inches. Find the length and the width.
In the following exercises, solve using the properties of triangles.
- A triangular flag has base of
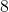 foot and height of
foot and height of 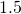 feet. What is its area?
feet. What is its area? - What is the base of a triangle with an area of
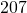 square inches and height of
square inches and height of 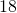 inches?
inches? - The perimeter of a triangular reflecting pool is
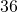 yards. The lengths of two sides are
yards. The lengths of two sides are 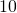 yards and
yards and 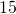 yards. How long is the third side?
yards. How long is the third side? - The perimeter of a triangle is
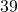 feet. One side of the triangle is
feet. One side of the triangle is 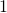 foot longer than the second side. The third side is
foot longer than the second side. The third side is 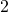 feet longer than the second side. Find the length of each side.
feet longer than the second side. Find the length of each side.
Answers
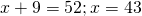
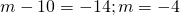
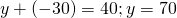
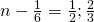
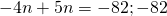
- 133=-19n; n=-7
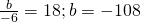
- 3/10x=15; x=50
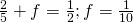
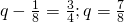
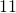 miles
miles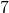 years old
years old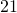 pounds
pounds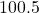 degrees
degrees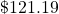
- 4
- 12
- -5
- 18,24
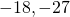
- 32,46
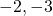
-
- 260 ft
- 3825 sq. ft
-
- 58 ft
- 210 sq. ft
- 24 inches
- 27 metres
- 23 m
- 7 in., 16 in.
- 17 m, 12 m
- 13.5 m, 12.8 m
- 25 ft, 50 ft
- 7 m, 11 m
- 26 in.
- 55 m
- 35 ft, 45 ft
- 76 in., 36 in.
- 6 sq. ft
- 23 in.
- 11 ft
- 12 ft, 13 ft, 14 ft