9 Financial Mathematics

9.2 Compound Interest

Learning Objectives

By the end of this section it is expected that you will be able to:

  • Determine the compound amount (future value) of an investment or loan
  • Determine the interest component of an investment or loan that involves compound interest
  • Determine the present value of a compound amount

Compound Interest

We have seen that with simple interest an investment will earn interest on the original amount. For an investment of $100 earning 10% simple interest, the interest earned after one year will be $10 since 10% of $100 = $10. An investment will grow more quickly if the interest  is calculated more often than once a year.  Interest will not only be calculated on the principal amount but also on the previously earned interest.  This process is referred to compounding.

Figure 1 illustrates the process of compounding or earning interest on interest. Consider an investment of $100 that earns 10%/year with interest being compounded semiannually.  With semiannual compounding the interest on the investment will be calculated twice during the year.

Fig. 1

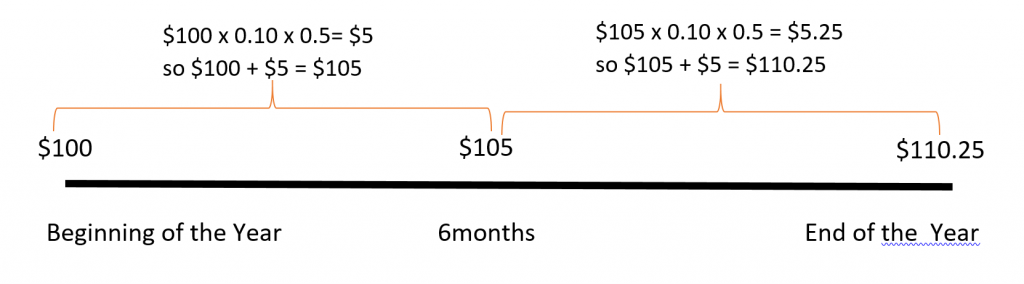
Using the simple interest formula I = Prt,  at the end of six months (half a year) interest will be calculated as follows:

I = $100 x 10% x 1/2 year = $5.

Adding this $5 to the principal of $100 you will have $105 at the end of the first six months. At the end of the year interest will be calculated again on the $105:

I = $105 x 10% x 1/2 year = $5.25.

Adding this $5.25 to $105 you will have $110.25 at the end of the year. In this case you would be earning interest not only on the original principal of $100, but also on the previously earned interest of $5. When interest is earned on interest, we say the interest is compounded. The total amount of principal and accumulated interest at the end of a loan or investment is called the compound amount. 

Consider a $100 investment that earns 10%/year compounded annually. The table in Figure 2 shows how the value of the $100 investment will grow over a 6-year period.

Year Amount at the beginning of the year Earned Interest Year End Total
1 $100 $10 $110
2 $110 $11 $121
3 $121 $12.10 $133.10
4 $133.10 $13.31 $146.41
5 $146.41 $14.64 $161.05
6 $161.05 $16.11 $177.16

Fig. 2

At the beginning of Year 1, $100 is invested, so the interest earned in the first year will be:

I = Prt = $100 × 0.10 × 1  = $10. This is added to the original $100 to result in $110 at the end of Year 1.

At the beginning of Year 2 the process will repeat but the principal P is now $110.

I = Prt = $110 × 0.10 ×1 = $11 in interest so at the end of Year 2 there will be:

$110 + $11 = $121 in the account.

Notice that the compound amount at the end of the six year period is $177.16.  The investment has earned an accumulated $77.16 in interest. If the investment had earned simple interest as opposed to compound interest it would have only earned:

I = Prt = 100 × 0.10 × 6 =  $60 in interest.

The above method of calculating the compound amount is very time consuming. Fortunately, there is a mathematical formula that we can use when working with compound interest.

Compound Interest Formula

The compound interest formula is:

A = P \left ( 1 + \frac{r}{n}\right )^{nt} where, A = total compound amount(includes principal and interest)
P = principal
r = annual interest rate
n = number of times in one year that interest is calculated
t = time (in years)

Since A includes both the principal and interest, to find the interest amount I calculate:
I = A - P

EXAMPLE 1

Find the compound amount and the interest earned on $100 compounded annually at 10% for 6 years.

Solution

P = $100

r = 10% = 0.1

n = 1 (since the interest is calculated once a year)

t = 6 years

 A = P \left ( 1 + \frac{r}{n}\right )^{nt}

A = 100 \left ( 1 + \frac{0.1}{1}\right )^{1 \times 6}

Replace the variables with their values
A = 100 \left ( 1 + 0.1\right )^{6} \frac{0.1}{1} = 0.1 and 1 \times 6 = 6
A = 100 \left ( 1.1 \right )^{6} Raise \left( 1.1 \right)^{6} = 177.1561
A = 100 \left ( 1.771 561 \right ) = 177.1561

The interest earned is A - P = \$ 177.16 - \$100 = $77.16

The compound amount is $177.16

TRY IT 1

Kyle won $10,000 in a lottery and deposited the full amount in a 3 year investment at 3.8% compounded annually. Find the compound amount and the interest earned over the three years.

Show answer

Compound Amount = $11,183.87; Interest = $1183.87

Interest can be compounded using a variety of compounding periods.   The compounding period is the span of time between when interest is calculated and when it will be calculated again. If there is one month between every interest calculation then the compounding period is monthly.  With monthly compounding there will be 12 compounding period in one year since there are twelve months in a year . The variable n in the compound interest formula reflects the number of times in one year that interest is calculated.

Compounding Periods

If interest is compounded:

annually  (once per year) ⇒ n = 1

semi-annually (twice a year)  ⇒ n = 2

quarterly (four times per year)  ⇒ n = 4

monthly  (twelve times per year)  ⇒ n = 12

weekly (fifty-two times per year)  ⇒ n = 52

daily  (three hundred sixty-five times per year) ⇒ n = 365

EXAMPLE 2

Find the compound amount and the interest earned on $500 compounded semiannually at 6% for 3 years.

Solution

P = \$ 500 A = P \left ( 1 + \frac{r}{n}\right )^{nt}
r = 6% = 0.06 A = 500 \left ( 1 + \frac{0.06}{2}\right )^{2 \times 3}
n = 2 (since the interest is calculated semiannually or 2 times a year) A = 500 \left ( 1 + \frac{0.06}{2}\right )^{6}
t = 3 A = 500 \left ( 1.03 \right )^{6}
A = 500 \left ( 1.19405 \right )

The compound amount is $597.03 and the interest earned is $597.03 – $500 = $97.03

TRY IT 2

Kam won $10,000 in a lottery and deposited the full amount in a 3 year investment at 3.8% compounded monthly. Find the compound amount and the interest earned over the three years.

Show answer

Compound Amount = $11,205.50; Interest = $1205.50

The greater the number of compounding periods in a year, the greater the total interest earned will be.

EXAMPLE 3

Find the compound amount and the interest earned on $500 compounded daily at 6% for 3 years.

Solution

P = \$ 500 A = P \left ( 1 + \frac{r}{n}\right )^{nt}
r = 6% = 0.06 A = 500 \left ( 1 + \frac{0.06}{365}\right )^{365 \times 3}
n = 365 (since the interest is calculated daily) A = 500 \left ( 1 + \frac{0.06}{365}\right )^{1095}
t = 3 A = 500 \left ( 1.000164 \right )^{1095}
A = 500 \left ( 1.1972 \right )

The compound amount is $598.60 and the interest earned is $598.60 – $500 = $98.60

TRY IT 3

Kam won $10,000 in a lottery and deposited the full amount in a 3 year investment at 3.8% compounded daily. Find the compound amount and the interest earned over the three years.

Show answer

Compound Amount = $11,207.45; Interest = $1207.45

Loan recipients must repay the principal amount borrowerd plus any interest charged. They will pay a greater price (in terms of total interest) when interest is  compounded.

EXAMPLE 4

Pat borrows $3200 an interest rate of  6.5% compounded semiannually. The original loan amount plus interest must be paid back in 3 years. Calculate the total amount that must be paid back in three years and determine the interest amount.

Solution

P = \$ 3200 A = P \left ( 1 + \frac{r}{n}\right )^{nt}
r = 6.5% = 0.065 A = 3200 \left ( 1 + \frac{0.065}{2}\right )^{2 \times 3}
n = 2 (since the interest is calculated semiannually or 2 times a year) A = 3200 \left ( 1 + \frac{0.065}{2}\right )^{6}
t = 3 A = 3200 \left ( 1.0325 \right )^{6}
A = 3200 \left ( 1.21155 \right )

The compound amount is $3876.95 and the interest owing is $3876.95 – $3200 = $676.95

TRY IT 4

Determine the compound interest on a 2 year loan of  $5000 at an interest rate of  4.8% compounded quarterly.

Show answer

Compound Amount = $5500.65; Interest = $500.65

EXAMPLE 5

Pat borrows $3200 an interest rate of  6.5% compounded monthly. The original loan amount plus interest must be paid back in 3 years. Calculate the total amount that must be paid back in three years and determine the interest amount.

Solution

P = \$ 3200 A = P \left ( 1 + \frac{r}{n}\right )^{nt}
r = 6.5% = 0.065 A = 3200 \left ( 1 + \frac{0.065}{12}\right )^{12 \times 3}
n = 12 (since the interest is calculated monthly or 12 times a year) A = 3200 \left ( 1 + \frac{0.065}{12}\right )^{36}
t = 3 A = 3200 \left ( 1.00542 \right )^{36}
A = 3200 \left ( 1.21467 \right )

The compound amount is $3886.95 and the interest owing is $3886.95 – $3200 = $686.95

TRY IT 5

Determine the compound interest on a 2 year loan of  $5000 at an interest rate of  4.8% compounded daily.

Show answer

Compound Amount = $5503.76; Interest = $503.76

Variation on Compound Interest – Present Value

We might want to know how much money we should invest now in order to make a purchase in the future.   Say for example that you want to know how much principal you needed to invest now in order to have $2000 in two years. The amount you need to invest now is called the present value of $2000. It is the amount of money that if invested now will accumulate to $2000 in two years. Assuming that your investment earns interest, the amount required now will be less than the future amount. Assuming annual compounding at an interest rate of 5% you will need to invest $1814.06 now to have $2000 in two years. Refer to Figure 3 below.

Present Value
Fig. 3

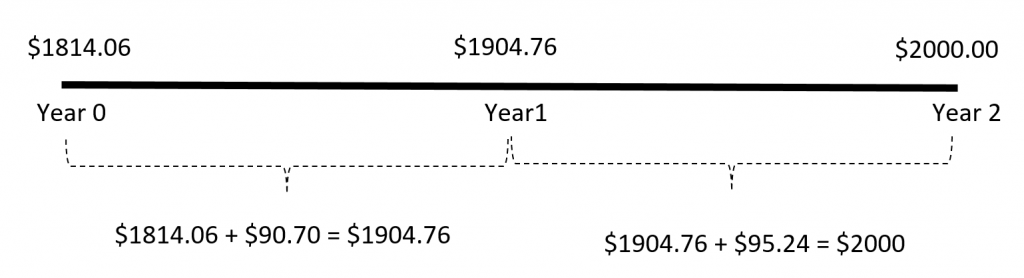
In Figure 3 we can see that at the beginning of the year $1814.06 is invested.

At the end of the first year the interest earned on $1814.06 is  5% × 1814.06 = $90.70.

At the end of the first year there will be $1904.76 in the account. In the second year the interest earned on $1904.76  is  $1904.76 × 0.05 = $95.24.

At th eend of the second year there will be $2000.00 in the account. The $2000 that is needed in two years is said to have a present value of $1814.06.

The present value can be calculated by solving the compound interest formula for P.

Formula for Present Value

The present value formula is:

P = \frac{A}{\left( 1 + \frac{r}{n} \right)^{nt}}

where P = present value
A = desired future amount
r = interest rate (as a decimal fraction)
n = number of times interest is calculated in one year
t = times (in years)

EXAMPLE 6

A house painting company is planning to expand its operations in three years time. It will require $24,000 in order to expand. How much must it invest now, at 4.6% interest compounded annually?

Solution

P = ?

A = $24000

r = 4.6% = 0.046

n = 1

 P = \frac{A}{\left( 1 + \frac{r}{n} \right)^{nt}}
t = 3 years P = \frac{24000}{\left( 1 + \frac{0.046}{1} \right)^{1 \times 3}} Replace the variables with their values
P = \frac{24000}{\left( 1.046\right)^{3}} Add 1+0.046= 1.046
P = \frac{24000}{1.144445} Raise \left( 1.046\right)^{3} = 1.144445
P = 20970.86

The present value is $20,970.86 so the company must invest that amount now to have $24,000 in three years.

TRY IT 6

Mae is planning on buying a vehicle when she turns 18 in five  years. How much money must she invest now in an account earning 7% interest, compounded annually, in order to afford a used vehicle at a cost of  $5000?

Show answer

An investment of $3564.93 is required

EXAMPLE 7

Pat and her friends are planning a reunion in five years.  She estimates that the cost of the trip plus expenses will be approximately $2000.  How much should she invest right now in order to have $2000 five years from now, if she knows her money will earn 6% compounded quarterly?

Solution

P = ?

A = $2000

r = 6% = 0.06

n = 4

 P = \frac{A}{\left( 1 + \frac{r}{n} \right)^{nt}}
t = 5 years P = \frac{2000}{\left( 1 + \frac{0.06}{4} \right)^{4 \times 5}} Replace the variables with their values
P = \frac{2000}{\left( 1 + \frac{0.06}{4} \right)^{20}} Multiply 4 \times 5 = 20
P = \frac{2000}{\left( 1 + 0.015 \right)^{20}} Divide \frac{0.06}{4}=0.015
P = \frac{2000}{\left( 1.015\right)^{20}} Add 1+0.015= 1.015
P = \frac{2000}{1.346855} Raise \left( 1.015 \right)^{20} = 1.346855
1484.94

The present value is $1484.94

In other words, if Pat invested $1484.94 now at 6% compounded quarterly, then in 5 years the compound amount would be $2000.

TRY IT 7

You are planning on attending college in four years and your parents plan to help out with $10,000  in assistance. How much money must they invest now in an account earning 5.6% compounded monthly if they plan to have $10000 in the account in four years?

Show answer

$7997.31

Key Concepts

  • to determine the compound amount (A)  of an investment or loan:
    • A = P \left ( 1 + \frac{r}{n}\right )^{nt}
  • to determine the interest component (I) of a principal or original amount (P) that has grown to a compound amount (A):
    • Interest = Compound Amount – Principal Amount    I = A – P
  • to determine the present value P of a compound amount the formula is:
    • P = \frac{A}{\left( 1 + \frac{r}{n} \right)^{nt}}
  • Compounding Periods
    • annually  (once per year) ⇒ n = 1
    • semi-annually (twice a year)  ⇒ n = 2
    • quarterly (four times per year)  ⇒ n = 4
    • monthly  (twelve times per year)  ⇒ n = 12
    • weekly (fifty-two times per year)  ⇒ n = 52
    • daily  (three hundred sixty-five times per year) ⇒ n = 365

Glossary

compound amount

is the total amount of principal and accumulated interest at the end of a loan or investment period.

compound interest

is when the interest on a loan or deposit is calculated based on both the initial principal and any accumulated interest from previous periods.

compounding period

is the span of time between when interest is calculated and when it will be calculated again.

present value

is the current value of a sum of money that has been invested and has grown to a larger compound amount.

9.2 Exercise Set

  1. Determine the value of n in each of the following:
    1. weekly, then n = ___________
    2. semi-annually, then n = ________
    3. quarterly, then n = _______
    4. daily, then n = _______
  2. Ada invested $1000 at 5% compounded annually.
    1. Complete the table below to determine the compound amount of Ada’s investment at the end of 5 years.
      Year Principal Amount Earned Interest Year End Total
      1 $1000 $50 $1050
      2 $1050 $52.50
      3
      4
      5
    2. Use the compound interest formula to determine the compound amount Ada will earn in 5 years.
  3. Find the compound amount and the earned interest when $1000 is invested under the following conditions:
    1. $1000 compounded annually at 9% for 5 years.
    2. $1000 compounded semi-annually at 9% for 5 years.
    3. $1000 compounded quarterly at 9% for 5 years.
    4. $1000 compounded monthly at 9% for 5 years.
    5. $1000 compounded daily at 9% for 5 years.
  4. When Penny was born her parents put $5000 in a special fund paying 4.4% compounded quarterly.
    1. How much will the fund be worth when Penny turns 10 years old?
    2. Penny’s parents take the money from the fund when Penny turns 10 and reinvest it at 7.2% componded monthly. How much will the investment be worth when Penny turns 18 years old?
  5. Anne’s parents invested  $8400 at 5% with daily compounding.  How much money will they have when Anne  starts  college in 5 years? How much interest did their investment accumulate over the 5 years?
  6. Theresa is considering two options for investing $10 000 : a savings account offering  8% simple interest or a savings certificate that earns 7.75% compounded monthly.
    1. How much will the savings account earn (in interest) in one year?
    2. How much interest will the savings certificate earn after one year?
    3. Which option yields more interest and by how much?
  7. You have $2500 to invest, compounded monthly, over a period of 4 years. Calculate the compound amount and the interest earned  when interest rates are as follows:
    1. 3%
    2. 6%
    3. 9%
    4. Notice that the interest rate of 9% is triple that of the 3% rate. How many times higher is the total interest earned at 9% than at the 3% rate?
  8. L. Shark says that he will lend you the $5000 you need but he wants 50% compounded daily on the loan. (Note that time t =  number of days/365)
    How much will you owe L. Shark if you pay the loan back in:

    1. 30 days
    2. 60 days
    3. 90 days
    4. How much more interest will you owe if you wait 90 days to pay back the loan rather than paying it back in 30 days? Does it make sense to pay off a loan quickly?
  9. For each of the following pairs of investment options, determine which option results in a higher compound amount.
    1. Option A: $8000 invested for 3 years at 2.6% compounded quarterlyOption B: $8000 invested for 2 years at 6.8% compounded monthly
    2. Option A: $20,000 invested for 7 years at 8.6% compounded annuallyOption B: $20,000 invested for 8 years at 7.4% compounded semiannually
  10. Find the present value for each of the following:
    1. $1800 due in 5 years at 4.6% compounded semi-annually.
    2. $2500 due in 2 years at 3.6% compounded monthly.
    3. $4000 due in 10 years at 8.4% compounded yearly.
    4. $650 due in one and one-half years at 4% compounded quarterly.
    5. $1000 due in 6 months at 2.8% compounded monthly.
  11. In 6 years, Sylvia’s son will be going to college.  Sylvia estimates that her son will need about $28000 to get started in the first year of his education.  How much should she invest now if she can earn 7% compounded semi-annually?
  12. The Smiths inherited $20,000.  They would like to spend some of the money now, but still have $20,000 ten years from now when they retire.  They have found  an investment that will earn them 8.4% compounded annually over this time.a. How much of the $20,000 should they invest now to guarantee that they will have $20,000 when they retire in 10 years?b. How much of the $20,000 can they spend now?
  13. A certain savings certificate will pay the owner $5000 in two years.  If the interest rate is 3.8% compounded weekly, how much will be invested now to accumulate to $5000 in two years?

Answers

    1. 52
    2. 2
    3. 4
    4. 265
    1. Year Principal Amount Earned Interest Year End Total
      1 $1000 $50 $1050
      2 $1050 $52.50 $1102.50
      3 $1102.50 $55.13 $1157.63
      4 $1157.63 $57.88 $1215.51
      5 $1215.51 $60.78 $1276.29
    1. $1276.28
    1. $1538.62;  $538.62
    2. $1552.97;  $552.97
    3. $1560.51;  $560.51
    4. $1565.68;  $565.68
    5. $1568.23;   $568.23
    1. $7744.91
    2. $13,753.79
  5. Compound Amount = $10, 785.63    Interest = $2385.63
    1. $800
    2. $803.13
    3. savings certificate pays $3.13 more interest
    1. Compound Amount = $2818.32 so interest =  $318.32
    2. Compound Amount = $3176.22  so interest = $676.22
    3. Compound Amount =  $3578.51   so interest = $1078.51
    4. $1078.51/$318.32 = 3.4 times as great
    1. $5209.61
    2. $5428.00
    3. $5655.55
    4. $445.96 so yes
    1. Option A $8646.80;  Option B  $9161.94 so Option B is better
    2. Option A $35,631.88;  Option B  $35,767.62 so Option B is better
    1. $1433.89
    2. $2326.58
    3. 1785.53
    4. $612.33
    5. $986.11
  11.  $18,529.93
  12. invest  $8927.65;  spend  $11072.35
  13. $4634.21

Attribution

Some of the content for this chapter is from “Unit 3: Compound interest” and “Unit 4: Variations on compound interest – present value” in Financial Mathematics by Paul Grinder, Velma McKay, Kim Moshenko, and Ada Sarsiat, which is under a CC BY 4.0 Licence.. Adapted by Kim Moshenko. See the Copyright page for more information.

License

Icon for the Creative Commons Attribution 4.0 International License

Business/Technical Mathematics Copyright © 2021 by Izabela Mazur and Kim Moshenko is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book