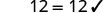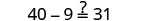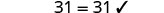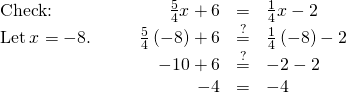2. Solving Linear Equations and Inequalities
2.1 Solve Linear Equations
Izabela Mazur; Lynn Marecek; and MaryAnne Anthony-Smith
Learning Objectives
By the end of this section it is expected that you will be able to:
- Verify a solution of an equation
- Solve equations using the Subtraction and Addition Properties of Equality
- Solve equations using the Division and Multiplication Properties of Equality
- Solve an equation with variables and constants on both sides
Verify a Solution of an Equation
Solving an equation is like discovering the answer to a puzzle. The purpose in solving an equation is to find the value or values of the variable that make each side of the equation the same – so that we end up with a true statement. Any value of the variable that makes the equation true is called a solution to the equation. It is the answer to the puzzle!
Solution of an equation
A solution of an equation is a value of a variable that makes a true statement when substituted into the equation.
HOW TO: Determine whether a number is a solution to an equation
- Substitute the number in for the variable in the equation.
- Simplify the expressions on both sides of the equation.
- Determine whether the resulting equation is true (the left side is equal to the right side).
- If it is true, the number is a solution.
- If it is not true, the number is not a solution.
EXAMPLE 1
Determine whether ![]() is a solution of
is a solution of ![]() .
.
Solution
Since a solution to an equation is a value of the variable that makes the equation true, begin by substituting the value of the solution for the variable.
| Substitute |
|
| Multiply. | |
| Simplify. |
Since ![]() results in a true statement (-7 is in fact equal to -7), -3 is a solution to the equation
results in a true statement (-7 is in fact equal to -7), -3 is a solution to the equation ![]() .
.
TRY IT 1
Is ![]() a solution of
a solution of ![]() ?
?
Show answer
no
There are many types of equations. In this chapter we will focus on solving linear equations.
Linear Equation
A linear equation is a first degree equation in one variable that can be written as:
Solve Equations Using the Subtraction and Addition Properties of Equality
Let us review all the properties that will help us to solve equations algebraically. The first one is the Subtraction Property of Equality.
Subtraction Property of Equality
For any numbers a, b, and c,
When you subtract the same quantity from both sides of an equation, you still have equality.
Let’s see how to use this property to solve an equation. Remember, the goal is to isolate the variable on one side of the equation. And we check our solutions by substituting the value into the equation to make sure we have a true statement.
EXAMPLE 2
Solve: ![]()
To get y by itself, we will undo the addition of 37 by using the Subtraction Property of Equality.
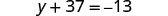 |
|
| Subtract 37 from each side to ‘undo’ the addition. | 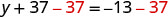 |
| Simplify. | 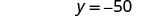 |
| Check: | 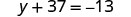 |
| Substitute |
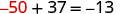 |
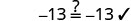 |
Since ![]() makes
makes ![]() a true statement, we have the solution to this equation.
a true statement, we have the solution to this equation.
TRY IT 2
Solve: ![]() .
.
Show answer
![]()
Addition Property of Equality
For any numbers a, b, and c,
When you add the same quantity to both sides of an equation, you still have equality.
In Example 2, 37 was added to the y and so we subtracted 37 to ‘undo’ the addition. In Example 3, we will need to ‘undo’ subtraction by using the Addition Property of Equality.
EXAMPLE 3
Solve: ![]()
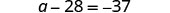 |
|
| Add 28 to each side to ‘undo’ the subtraction. | 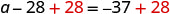 |
| Simplify. | 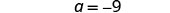 |
| Check: | 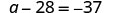 |
| Substitute |
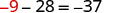 |
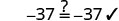 |
|
| The solution to |
TRY IT 3
Solve: ![]()
Show answer
![]()
EXAMPLE 4
Solve: ![]()
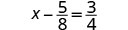 |
|
| Use the Addition Property of Equality. | 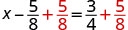 |
| Find the LCD to add the fractions on the right. | 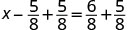 |
| Simplify. | 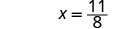 |
| Check: | 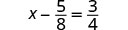 |
| Substitute |
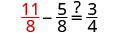 |
| Subtract. | 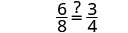 |
| Simplify. | 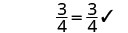 |
| The solution to |
TRY IT 4
Solve: ![]()
Show answer
![]()
The next example will be an equation with decimals.
EXAMPLE 5
Solve: ![]()
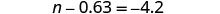 |
|
| Use the Addition Property of Equality. |  |
| Add. | 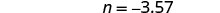 |
| Check: | 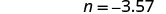 |
| Let |
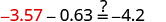 |
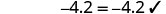 |
TRY IT 5
Solve: ![]()
Show answer
![]()
Solve Equations Using the Division and Multiplication Properties of Equality
You may have noticed that all of the equations we have solved so far have been of the form ![]() or
or ![]() . We were able to isolate the variable by adding or subtracting the constant term on the side of the equation with the variable. Now we will see how to solve equations that have a variable multiplied by a constant and so will require division to isolate the variable.To solve those kind of equations we will use the Division Property of Equality.
. We were able to isolate the variable by adding or subtracting the constant term on the side of the equation with the variable. Now we will see how to solve equations that have a variable multiplied by a constant and so will require division to isolate the variable.To solve those kind of equations we will use the Division Property of Equality.
The Division Property of Equality
For any numbers a, b, and c, and ![]() ,
,
The goal in solving an equation is to ‘undo’ the operation on the variable. In the next example, the variable is multiplied by 5, so we will divide both sides by 5 to ‘undo’ the multiplication.
EXAMPLE 6
Solve: ![]()
| To isolate |
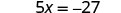 |
| Divide to ‘undo’ the multiplication. | 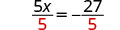 |
| Simplify. | 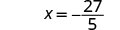 |
| Check: | 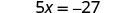 |
| Substitute |
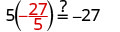 |
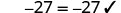 |
|
| Since this is a true statement, is the solution to |
TRY IT 6
Solve: ![]()
Show answer
![]()
Consider the equation ![]() . We want to know what number divided by 4 gives 3. So to “undo” the division, we will need to multiply by 4. The Multiplication Property of Equality will allow us to do this. This property says that if we start with two equal quantities and multiply both by the same number, the results are equal.
. We want to know what number divided by 4 gives 3. So to “undo” the division, we will need to multiply by 4. The Multiplication Property of Equality will allow us to do this. This property says that if we start with two equal quantities and multiply both by the same number, the results are equal.
The Multiplication Property of Equality
For any numbers a, b, and c,
If you multiply both sides of an equation by the same number, you still have equality.
EXAMPLE 7
Solve: ![]()
Here ![]() is divided by
is divided by ![]() . We must multiply by
. We must multiply by ![]() to isolate
to isolate ![]() .
.
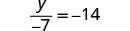 |
|
| Multiply both sides by |
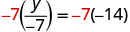 |
| Multiply. | 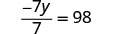 |
| Simplify. | 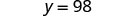 |
| Check. | |
| Substitute |
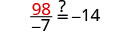 |
| Divide | 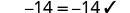 |
TRY IT 7
Solve: ![]()
Show answer
![]()
EXAMPLE 8
Solve: ![]()
Since the product of a number and its reciprocal is 1, our strategy will be to isolate ![]() by multiplying by the reciprocal of
by multiplying by the reciprocal of ![]() .
.
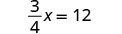 |
|
| Multiply by the reciprocal of |
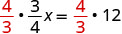 |
| Reciprocals multiply to 1. | 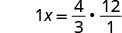 |
| Multiply. | 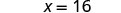 |
| Notice that we could have divided both sides of the equation |
|
| Check: | 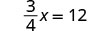 |
| Substitute |
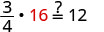
|
TRY IT 8
Solve: ![]()
Show answer
![]()
Now we have covered all four properties of equality—subtraction, addition, division, and multiplication. We’ll list them all together here for easy reference.
Properties of Equality
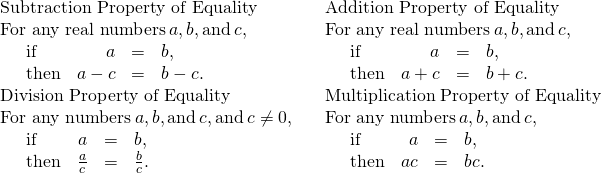
When you add, subtract, multiply, or divide the same quantity from both sides of an equation, you still have equality.
Now we will use those properties to solve equations in which the variable terms, or constant terms, or both are on both sides of the equation.
Solve Equations with Variables and Constants on Both Sides
Our strategy will involve choosing one side of the equation to be the “variable side”, and the other side of the equation to be the “constant side.” Then, we will use the Subtraction and Addition Properties of Equality to get all the variable terms together on one side of the equation and the constant terms together on the other side.
By doing this, we will transform the equation that began with variables and constants on both sides into the form ![]() We already know how to solve equations of this form by using the Division or Multiplication Properties of Equality.
We already know how to solve equations of this form by using the Division or Multiplication Properties of Equality.
EXAMPLE 9
Solve: ![]()
Solution
In this equation, the variable is found only on the left side. It makes sense to call the left side the “variable” side. Therefore, the right side will be the “constant” side. We will write the labels above the equation to help us remember what goes where. Since the left side is the “variable” side, the 9 is out of place. It is subtracted from the ![]() , so to “undo” subtraction, add 9 to both sides. Remember, whatever you do to the left, you must do to the right.
, so to “undo” subtraction, add 9 to both sides. Remember, whatever you do to the left, you must do to the right.
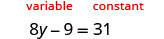 |
|
| Add 9 to both sides. | 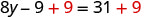 |
| Simplify. | 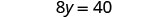
The variables are now on one side and the constants on the other. We continue from here as we did earlier. |
| Divide both sides by 8. | 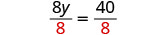 |
| Simplify. | 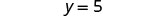 |
| Check. | 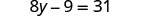 |
| Let |
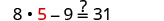
|
TRY IT 9
Solve: ![]()
Show answer
![]()
What if there are variables on both sides of the equation? For equations like this, begin as we did above—choose a “variable” side and a “constant” side, and then use the subtraction and addition properties of equality to collect all variables on one side and all constants on the other side.
EXAMPLE 10
Solve: ![]()
The only constant is on the left and the ![]() ’s are on both sides. Let’s leave the constant on the left and get the variables to the right.
’s are on both sides. Let’s leave the constant on the left and get the variables to the right.
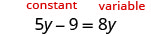 |
|
| Subtract |
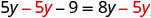 |
| Simplify. | 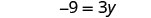 |
| We have the y’s on the right and the constants on the left. Divide both sides by 3. |
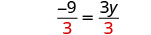 |
| Simplify. | 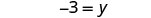 |
| Check: | 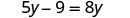 |
| Let |
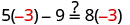 |
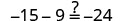 |
|
TRY IT 10
Solve: ![]()
Show answer
![]()
The next example will be the first to have variables and constants on both sides of the equation. It may take several steps to solve this equation, so we need a clear and organized strategy.
EXAMPLE 11
Solve: ![]()





TRY IT 11
Solve: ![]()
Show answer
![]()
We’ll list the steps below so you can easily refer to them. But we’ll call this the ‘Beginning Strategy’ because we’ll be adding some steps later in this chapter.
HOW TO: Equations with variables and constants on both sides of the equation (beginning strategy)
- Choose which side will be the “variable” side—the other side will be the “constant” side.
- Collect the variable terms to the “variable” side of the equation, using the Addition or Subtraction Property of Equality.
- Collect all the constants to the other side of the equation, using the Addition or Subtraction Property of Equality.
- Make the coefficient of the variable equal 1, using the Multiplication or Division Property of Equality.
- Check the solution by substituting it into the original equation.
In Step 1, a helpful approach is to make the “variable” side the side that has the variable with the larger coefficient. This usually makes the arithmetic easier.
EXAMPLE 12
Solve: ![]()
In the first step, choose the variable side by comparing the coefficients of the variables on each side.
Since ![]() >
> ![]() , make the right side the “variable” side and the left side the “constant” side.
, make the right side the “variable” side and the left side the “constant” side.
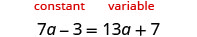 |
|
| Subtract |
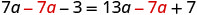 |
| Combine like terms. | 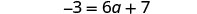 |
| Subtract |
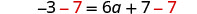 |
| Simplify. | 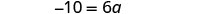 |
| Divide both sides by |
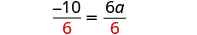 |
| Simplify. | 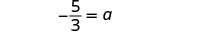 |
| Check: | 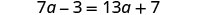 |
| Let |
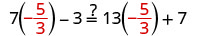 |
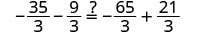 |
|
TRY IT 12
Solve: ![]()
Show answer
![]()
To solve an equation with fractions, we just follow the steps of our strategy to get the solution!
EXAMPLE 13
Solve: ![]()
Since ![]() >
> ![]() , make the left side the “variable” side and the right side the “constant” side.
, make the left side the “variable” side and the right side the “constant” side.
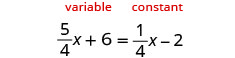 |
||
| Subtract |
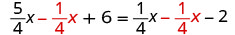 |
|
| Combine like terms. | 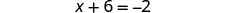 |
|
| Subtract |
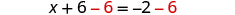 |
|
| Simplify. | 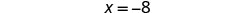
|
|
TRY IT 13
Solve: ![]()
Show answer
![]()
We will use the same strategy to find the solution for an equation with decimals.
EXAMPLE 14
Solve: ![]()
Since ![]() >
> ![]() , make the left side the “variable” side and the right side the “constant” side.
, make the left side the “variable” side and the right side the “constant” side.
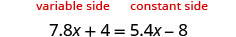 |
|
| Subtract |
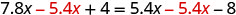 |
| Combine like terms. | 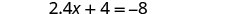 |
| Subtract |
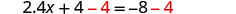 |
| Simplify. | 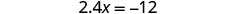 |
| Use the Division Propery of Equality. | 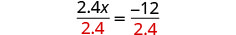 |
| Simplify. | 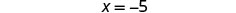 |
| Check: | 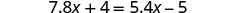 |
| Let |
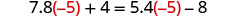 |
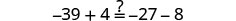 |
|
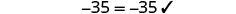 |
TRY IT 14
Solve: ![]()
Show answer
![]()
Key Concepts
- To determine whether a number is a solution to an equation
- Substitute the number in for the variable in the equation.
- Simplify the expressions on both sides of the equation.
- Determine whether the resulting statement is true.
- If it is true, the number is a solution.
- If it is not true, the number is not a solution.
- The addition property of equality
- For any numbers a, b, and c, if
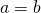 , then
, then 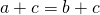 .
.
- For any numbers a, b, and c, if
- The subtraction property of equality
- For any numbers a, b, and c, if
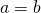 , then
, then 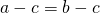 .
.
- For any numbers a, b, and c, if
- The division property of equality
- For any numbers a, b, and c, and
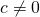 , if
, if 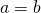 , then
, then 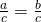 .
.
When you divide both sides of an equation by any non-zero number, you still have equality.
- For any numbers a, b, and c, and
- The multiplication property of equality
- For any numbers a, b, and c, if a = b then ac = bc.
Glossary
solution of an equation
A value of a variable that makes a true statement when substituted into the equation.
2.1 Exercise Set
In the following exercises, determine whether the given value is a solution to the equation.
- Is
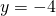 a solution of
a solution of 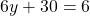 ?
? - Is
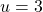 a solution of
a solution of 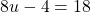 ?
?
In the following exercises, solve each equation using the Subtraction and Addition Properties of Equality.
In the following exercises, solve each equation using the Division and Multiplication Properties of Equality and check the solution.
In the following exercises, solve the following equations with constants on both sides.
Answers
Attributions
This chapter has been adapted from “Solve Equations Using the Subtraction and Addition Properties of Equality” in Elementary Algebra (OpenStax) by Lynn Marecek and MaryAnne Anthony-Smith, which is under a CC BY 4.0 Licence. Adapted by Izabela Mazur. See the Adaptation Statement for more information.