1. Operations with Real Numbers
1.5. Exponents and Scientific Notation
Learning Objectives
By the end of this section it is expected that you will be able to:
- Simplify expressions with exponents
- Simplify expressions with zero exponents
- Use the definition of a negative exponent
- Use formulas with exponents in applications
- Convert from decimal notation to scientific notation
- Convert scientific notation to decimal form
- Multiply and divide using scientific notation
Simplify Expressions with Exponents
Remember that an exponent indicates repeated multiplication of the same quantity. For example, ![]() means to multiply 2 by itself 4 times, so
means to multiply 2 by itself 4 times, so ![]() means 2 · 2 · 2 · 2
means 2 · 2 · 2 · 2
Let’s review the vocabulary for expressions with exponents.
Exponential Notation (Power)
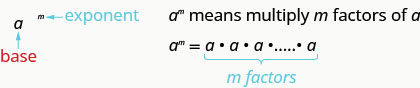
This is read ![]() to the
to the ![]() power.
power.
In the expression ![]() , the exponent
, the exponent ![]() tells us how many times we use the base
tells us how many times we use the base ![]() as a factor.
as a factor.

Before we begin working with expressions containing exponents, let’s simplify a few expressions involving only numbers.
EXAMPLE 1
Simplify: a) ![]() b)
b) ![]() c)
c) ![]() d)
d) ![]() .
.
| a) | |
| Multiply three factors of 4. | 4 · 4 · 4 |
| Simplify. | |
| b) | |
| Multiply one factor of 7. | |
| c) | |
| Multiply two factors. | |
| Simplify. | |
| d) | |
| Multiply two factors. | |
| Simplify. |
TRY IT 1
Simplify: a) ![]() b)
b) ![]() c)
c) ![]() d)
d) ![]() .
.
Show answer
a) 216 b) ![]() c)
c) ![]() d) 0.1849
d) 0.1849
TRY IT 2
Simplify: a) ![]() b)
b) ![]() .
.
Show answer
a) ![]() b)
b) ![]()
Notice the similarities and differences in (Example 2) a) and (Example 2) b)! Why are the answers different? As we follow the order of operations in part a) the parentheses tell us to raise the ![]() to the 4th power. In part b) we raise just the 5 to the 4th power and then take the opposite.
to the 4th power. In part b) we raise just the 5 to the 4th power and then take the opposite.
 .You should get 0.16807.
.You should get 0.16807.Simplify Expressions with an Exponent of Zero
When simplifying expressions with exponents we very often use the Product Property and the Quotient Property.
Product Property for Exponents
If ![]() is a real number, and
is a real number, and ![]() and
and ![]() are counting numbers, then
are counting numbers, then
To multiply with like bases, add the exponents.
An example with numbers helps to verify this property.
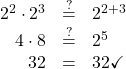
Quotient Property for Exponents
If ![]() is a real number,
is a real number, ![]() , and
, and ![]() and
and ![]() are whole numbers, then
are whole numbers, then
A couple of examples with numbers may help to verify this property.
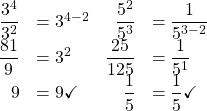
A special case of the Quotient Property is when the exponents of the numerator and denominator are equal, such as an expression like ![]() . From your earlier work with fractions, you know that:
. From your earlier work with fractions, you know that:
![]()
In words, a number divided by itself is 1. So, ![]() , for any
, for any ![]() , since any number divided by itself is 1
, since any number divided by itself is 1
The Quotient Property for Exponents shows us how to simplify ![]() when
when ![]() >
> ![]() and when
and when ![]() <
< ![]() by subtracting exponents. What if
by subtracting exponents. What if ![]() ?
?
Consider ![]() , which we know is 1
, which we know is 1
| Write |
|
| Subtract exponents. | |
| Simplify. |
Now we will simplify ![]() in two ways to lead us to the definition of the zero exponent. In general, for
in two ways to lead us to the definition of the zero exponent. In general, for ![]() :
:
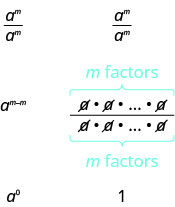
We see ![]() simplifies to
simplifies to ![]() and to 1. So
and to 1. So ![]() .
.
Zero Exponent
If ![]() is a non-zero number, then
is a non-zero number, then ![]() .
.
Any nonzero number raised to the zero power is 1
Simplify: ![]() .
.
The definition says any non-zero number raised to the zero power is 1
| Use the definition of the zero exponent. |
TRY IT 3
Simplify: ![]()
Show answer
1
Now that we have defined the zero exponent, we can expand all the Properties of Exponents to include whole number exponents.
Use the Definition of a Negative Exponent
Now, let’s use the definition of a negative exponent to simplify expressions.
Negative Exponent
If ![]() is an integer and
is an integer and ![]() , then
, then ![]() .
.
The negative exponent tells us we can re-write the expression by taking the reciprocal of the base and then changing the sign of the exponent.
Any expression that has negative exponents is not considered to be in simplest form. We will use the definition of a negative exponent and other properties of exponents to write the expression with only positive exponents.
EXAMPLE 4
Simplify: a) ![]() b)
b) ![]() .
.
| a) | |
| Use the definition of a negative exponent, |
|
| Simplify. | |
| b) | |
| Use the definition of a negative exponent, |
|
| Simplify. |
TRY IT 4
Simplify: a) ![]() b)
b) ![]() .
.
Show answer
a) ![]() b)
b) ![]()
In (Example 4) we raised an integer to a negative exponent. What happens when we raise a fraction to a negative exponent? We’ll start by looking at what happens to a fraction whose numerator is one and whose denominator is an integer raised to a negative exponent.
| Use the definition of a negative exponent, |
|
| Simplify the complex fraction. | |
| Multiply. |
This leads to the Property of Negative Exponents.
Property of Negative Exponents
If ![]() is an integer and
is an integer and ![]() , then
, then ![]() .
.
EXAMPLE 5
Simplify: ![]() .
.
| Use the property of a negative exponent, |
|
| Simplify. |
TRY IT 5
Simplify: ![]() .
.
Show answer
![]()
Suppose now we have a fraction raised to a negative exponent. Let’s use our definition of negative exponents to lead us to a new property.
| Use the definition of a negative exponent, |
|
| Simplify the denominator. | |
| Simplify the complex fraction. | |
| But we know that |
|
| This tells us that: |
To get from the original fraction raised to a negative exponent to the final result, we took the reciprocal of the base—the fraction—and changed the sign of the exponent.
This leads us to the Quotient to a Negative Power Property.
Quotient to a Negative Exponent Property
If ![]() are real numbers,
are real numbers, ![]() , and
, and ![]() is an integer, then
is an integer, then ![]() .
.
EXAMPLE 6
Simplify: ![]() .
.
| Use the Quotient to a Negative Exponent Property, |
|
| Take the reciprocal of the fraction and change the sign of the exponent. | |
| Simplify. |
TRY IT 6
Simplify: ![]() .
.
Show answer
![]()
When simplifying an expression with exponents, we must be careful to correctly identify the base.
EXAMPLE 7
Simplify: a) ![]() b)
b) ![]() c)
c) ![]() d)
d) ![]() .
.
| a) Here the exponent applies to the base |
|
| Take the reciprocal of the base and change the sign of the exponent. | |
| Simplify. | |
| b) The expression |
|
| Rewrite as a product with |
|
| Take the reciprocal of the base and change the sign of the exponent. | |
| Simplify. | |
| c) Here the exponent applies to the base |
|
| Take the reciprocal of the base and change the sign of the exponent. | |
| Simplify. | |
| d) The expression |
|
| Rewrite as a product with |
|
| Take the reciprocal of the base and change the sign of the exponent. | |
| Simplify. |
TRY IT 7
Simplify: a) ![]() b)
b) ![]() c)
c) ![]() d)
d) ![]() .
.
Show answer
a) ![]() b)
b) ![]() c) 25 d)
c) 25 d) ![]()
We must be careful to follow the Order of Operations. In the next example, parts (a) and (b) look similar, but the results are different.
EXAMPLE 8
Simplify: a) ![]() b)
b) ![]() .
.
| a) Do exponents before multiplication. |
|
| Use |
|
| Simplify. | |
| b) | |
| Simplify inside the parentheses first. | |
| Use |
|
| Simplify. |
TRY IT 8
Simplify: a) ![]() b)
b) ![]() .
.
Show answer
a) ![]() b)
b) ![]()
Use Formulas with Exponents in Applications
In this section, we will use geometry formulas that contain exponents to solve problems. Since we will be solving applications, we will once again show our Problem-Solving Strategy for Geometry Applications.
Problem Solving Strategy for Geometry Applications
- Read the problem and make sure you understand all the words and ideas. Draw the figure and label it with the given information.
- Identify what you are looking for.
- Name what you are looking for. Choose a variable to represent that quantity.
- Translate into an equation by writing the appropriate formula or model for the situation. Substitute in the given information.
- Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
A cube is a rectangular solid whose length, width, and height are equal. See Volume and Surface Area of a Cube, below. Substituting, s for the length, width and height into the formulas for volume and surface area of a rectangular solid, we get:
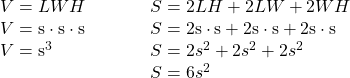
So for a cube, the formulas for volume and surface area are ![]() and
and ![]() .
.
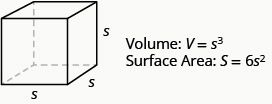
Volume and Surface Area of a Cube
For any cube with sides of length ![]() ,
,
EXAMPLE 3
A cube is ![]() inches on each side. Find its a) volume and b) surface area.
inches on each side. Find its a) volume and b) surface area.
Step 1 is the same for both a) and b), so we will show it just once.
| Step 1. Read the problem. Draw the figure and label it with the given information. |
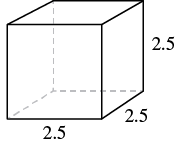 |
| a) | |
| Step 2. Identify what you are looking for. | the volume of the cube |
| Step 3. Name. Choose a variable to represent it. | let V = volume |
| Step 4. Translate. Write the appropriate formula. |
|
| Step 5. Solve. Substitute and solve. | |
| Step 6. Check: Check your work. | |
| Step 7. Answer the question. | The volume is 15.625 cubic inches. |
| b) | |
| Step 2. Identify what you are looking for. | the surface area of the cube |
| Step 3. Name. Choose a variable to represent it. | let S = surface area |
| Step 4. Translate. Write the appropriate formula. |
|
| Step 5. Solve. Substitute and solve. | |
| Step 6. Check: The check is left to you. | |
| Step 7. Answer the question. | The surface area is 37.5 square inches. |
TRY IT 3
For a cube with side 4.5 metres, find the a) volume and b) surface area of the cube.
Show answer
- 91.125 cu. m
- 121.5 sq. m
EXAMPLE 4
A notepad cube measures ![]() inches on each side. Find its a) volume and b) surface area.
inches on each side. Find its a) volume and b) surface area.
| Step 1. Read the problem. Draw the figure and label it with the given information. |
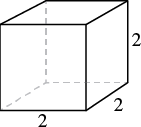 |
| a) | |
| Step 2. Identify what you are looking for. | the volume of the cube |
| Step 3. Name. Choose a variable to represent it. | let V = volume |
| Step 4. Translate. Write the appropriate formula. |
|
| Step 5. Solve the equation. | |
| Step 6. Check: Check that you did the calculations correctly. |
|
| Step 7. Answer the question. | The volume is 8 cubic inches. |
| b) | |
| Step 2. Identify what you are looking for. | the surface area of the cube |
| Step 3. Name. Choose a variable to represent it. | let S = surface area |
| Step 4. Translate. Write the appropriate formula. |
|
| Step 5. Solve the equation. | |
| Step 6. Check: The check is left to you. | |
| Step 7. Answer the question. | The surface area is 24 square inches. |
TRY IT 4
A packing box is a cube measuring ![]() feet on each side. Find its a) volume and b) surface area.
feet on each side. Find its a) volume and b) surface area.
Show answer
- 64 cu. ft
- 96 sq. ft
A sphere is the shape of a basketball, like a three-dimensional circle. Just like a circle, the size of a sphere is determined by its radius, which is the distance from the center of the sphere to any point on its surface. The formulas for the volume and surface area of a sphere are given below.
Showing where these formulas come from, like we did for a rectangular solid, is beyond the scope of this course. We will approximate ![]() with
with ![]() .
.
Volume and Surface Area of a Sphere
For a sphere with radius ![]()

EXAMPLE 5
A sphere has a radius ![]() inches. Find its a) volume and b) surface area.
inches. Find its a) volume and b) surface area.
Step 1 is the same for both a) and b), so we will show it just once.
| Step 1. Read the problem. Draw the figure and label it with the given information. |
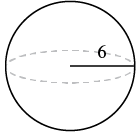 |
| a) | |
| Step 2. Identify what you are looking for. | the volume of the sphere |
| Step 3. Name. Choose a variable to represent it. | let V = volume |
| Step 4. Translate. Write the appropriate formula. |
|
| Step 5. Solve. | |
| Step 6. Check: Double-check your math on a calculator. | |
| Step 7. Answer the question. | The volume is approximately 904.32 cubic inches. |
| b) | |
| Step 2. Identify what you are looking for. | the surface area of the cube |
| Step 3. Name. Choose a variable to represent it. | let S = surface area |
| Step 4. Translate. Write the appropriate formula. |
|
| Step 5. Solve. | |
| Step 6. Check: Double-check your math on a calculator | |
| Step 7. Answer the question. | The surface area is approximately 452.16 square inches. |
TRY IT 5
Find the a) volume and b) surface area of a sphere with radius 3 centimetres.
Show answer
- 113.04 cu. cm
- 113.04 sq. cm
EXAMPLE 6
A globe of Earth is in the shape of a sphere with radius ![]() centimetres. Find its a) volume and b) surface area. Round the answer to the nearest hundredth.
centimetres. Find its a) volume and b) surface area. Round the answer to the nearest hundredth.
| Step 1. Read the problem. Draw a figure with the given information and label it. |
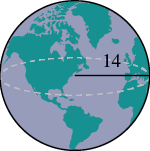 |
| a) | |
| Step 2. Identify what you are looking for. | the volume of the sphere |
| Step 3. Name. Choose a variable to represent it. | let V = volume |
| Step 4. Translate. Write the appropriate formula. Substitute. (Use 3.14 for |
|
| Step 5. Solve. | |
| Step 6. Check: We leave it to you to check your calculations. | |
| Step 7. Answer the question. | The volume is approximately 11,488.21 cubic inches. |
| b) | |
| Step 2. Identify what you are looking for. | the surface area of the sphere |
| Step 3. Name. Choose a variable to represent it. | let S = surface area |
| Step 4. Translate. Write the appropriate formula. Substitute. (Use 3.14 for |
|
| Step 5. Solve. | |
| Step 6. Check: We leave it to you to check your calculations. | |
| Step 7. Answer the question. | The surface area is approximately 2461.76 square inches. |
TRY IT 6
A beach ball is in the shape of a sphere with radius of ![]() inches. Find its a) volume and b) surface area.
inches. Find its a) volume and b) surface area.
Show answer
- 3052.08 cu. in.
- 1017.36 sq. in.
Convert from Decimal Notation to Scientific Notation
Remember working with place value for whole numbers and decimals? Our number system is based on powers of 10. We use tens, hundreds, thousands, and so on. Our decimal numbers are also based on powers of tens—tenths, hundredths, thousandths, and so on. Consider the numbers 4,000 and ![]() . We know that 4,000 means
. We know that 4,000 means ![]() and 0.004 means
and 0.004 means ![]() .
.
If we write the 1000 as a power of ten in exponential form, we can rewrite these numbers in this way:

When a number is written as a product of two numbers, where the first factor is a number greater than or equal to one but less than 10, and the second factor is a power of 10 written in exponential form, it is said to be in scientific notation.
Scientific Notation
A number is expressed in scientific notation when it is of the form
It is customary in scientific notation to use as the ![]() multiplication sign, even though we avoid using this sign elsewhere in algebra.
multiplication sign, even though we avoid using this sign elsewhere in algebra.
If we look at what happened to the decimal point, we can see a method to easily convert from decimal notation to scientific notation.

In both cases, the decimal was moved 3 places to get the first factor between 1 and 10
![]()
EXAMPLE 9
Write in scientific notation: 37,000.




TRY IT 9
Write in scientific notation: ![]() .
.
Show answer
![]()
- Move the decimal point so that the first factor is greater than or equal to 1 but less than 10.
- Count the number of decimal places, n, that the decimal point was moved.
- Write the number as a product with a power of 10.
If the original number is:
- greater than 1, the power of 10 will be 10n.
- between 0 and 1, the power of 10 will be 10−n.
- Check.
EXAMPLE 10
Write in scientific notation: ![]() .
.
The original number, ![]() , is between 0 and 1 so we will have a negative power of 10
, is between 0 and 1 so we will have a negative power of 10
| Move the decimal point to get 5.2, a number between 1 and 10. | |
| Count the number of decimal places the point was moved. | |
| Write as a product with a power of 10. | |
| Check. | |
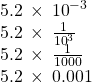 |
|
TRY IT 10
Write in scientific notation: ![]() .
.
Show answer
![]()
Convert Scientific Notation to Decimal Form
How can we convert from scientific notation to decimal form? Let’s look at two numbers written in scientific notation and see.

If we look at the location of the decimal point, we can see an easy method to convert a number from scientific notation to decimal form.
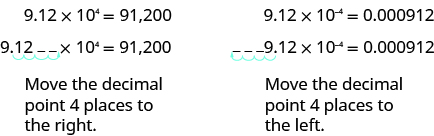
In both cases the decimal point moved 4 places. When the exponent was positive, the decimal moved to the right. When the exponent was negative, the decimal point moved to the left.
EXAMPLE 11
Convert to decimal form: ![]() .
.



TRY IT 11
Convert to decimal form: ![]() .
.
Show answer
1,300
The steps are summarized below.
To convert scientific notation to decimal form:
- Determine the exponent,
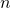 , on the factor 10.
, on the factor 10. - Move the decimal
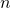 places, adding zeros if needed.
places, adding zeros if needed.
- If the exponent is positive, move the decimal point
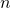 places to the right.
places to the right. - If the exponent is negative, move the decimal point
 places to the left.
places to the left.
- If the exponent is positive, move the decimal point
- Check.
EXAMPLE 12
Convert to decimal form: ![]() .
.
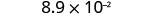 |
|
| Determine the exponent, n, on the factor 10. |  |
| Since the exponent is negative, move the decimal point 2 places to the left. | 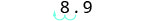 |
| Add zeros as needed for placeholders. | 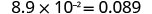 |
TRY IT 12
Convert to decimal form: ![]() .
.
Show answer
0.00012
Multiply and Divide Using Scientific Notation
Astronomers use very large numbers to describe distances in the universe and ages of stars and planets. Chemists use very small numbers to describe the size of an atom or the charge on an electron. When scientists perform calculations with very large or very small numbers, they use scientific notation. Scientific notation provides a way for the calculations to be done without writing a lot of zeros. We will see how the Properties of Exponents are used to multiply and divide numbers in scientific notation.
EXAMPLE 13
Multiply. Write answers in decimal form: ![]() .
.
| Use the Commutative Property to rearrange the factors. | |
| Multiply. | |
| Change to decimal form by moving the decimal two places left. |
TRY IT 13
Multiply ![]() . Write answers in decimal form.
. Write answers in decimal form.
Show answer
0.06
EXAMPLE 14
Multiply. Write answer in scientific notation: ![]() .
.
| Use the Commutative Property to rearrange the factors. | |
| Multiply. | |
| Write the answer in scientific notation. |
|
TRY IT 14
Multiply. Write answer in scientific notation: ![]() .
.
Show answer
\(2.133\times{10}^{-2}\)
EXAMPLE 15
Divide. Write answers in decimal form: ![]() .
.
| Separate the factors, rewriting as the product of two fractions. | |
| Divide. | |
| Change to decimal form by moving the decimal five places right. | |
TRY IT 15
Divide ![]() . Write answers in decimal form.
. Write answers in decimal form.
Show answer
400,000
EXAMPLE 16
Divide. Write answer in scientific notation: ![]() .
.
| Separate the factors, rewriting as the product of two fractions. | |
| Divide. | |
| Write answer in scientific notation | |
TRY IT 16
Divide ![]() . Write answer in scientific notation.
. Write answer in scientific notation.
Show answer
![]()
Access these online resources for additional instruction and practice with integer exponents and scientific notation:
Key Concepts
- Exponential Notation
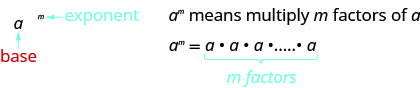
- Product Property of Exponents
- If
 are real numbers and
are real numbers and 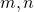 are whole numbers, then
are whole numbers, then
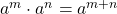
- If
- Quotient Property for Exponents:
- If
 is a real number,
is a real number, 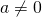 , and
, and 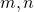 are whole numbers, then:
are whole numbers, then:
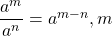 >
> 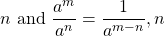 >
> 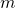
- If
- Zero Exponent
- If
 is a non-zero number, then
is a non-zero number, then 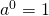 .
.
- If
- Property of Negative Exponents
- If
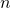 is a positive integer and
is a positive integer and 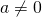 , then
, then 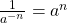
- If
- Quotient to a Negative Exponent
- If
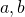 are real numbers,
are real numbers, 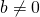 and
and 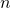 is an integer , then
is an integer , then 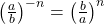
- If
- To convert a decimal to scientific notation:
- Move the decimal point so that the first factor is greater than or equal to 1 but less than 10.
- Count the number of decimal places,
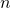 , that the decimal point was moved.
, that the decimal point was moved. - Write the number as a product with a power of 10. If the original number is:
- greater than 1, the power of 10 will be
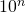
- between 0 and 1, the power of 10 will be
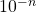
- greater than 1, the power of 10 will be
- Check.
- To convert scientific notation to decimal form:
- Determine the exponent,
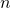 , on the factor 10.
, on the factor 10. - Move the decimal
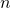 places, adding zeros if needed.
places, adding zeros if needed.
- If the exponent is positive, move the decimal point
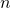 places to the right.
places to the right. - If the exponent is negative, move the decimal point
 places to the left.
places to the left.
- If the exponent is positive, move the decimal point
- Check
- Determine the exponent,
1.5 Exercise Set
In the following exercises, simplify each expression with exponents.
In the following exercises, simplify.
In the following exercises, find a) the volume and b) the surface area of the cube with the given side length.
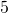 centimetres
centimetres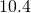 feet
feet
In the following exercises, solve.
- Museum A cube-shaped museum has sides
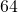 metres long. Find its a) volume and b) surface area.
metres long. Find its a) volume and b) surface area. - Base of statue The base of a statue is a cube with sides
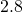 metres long. Find its a) volume and b) surface area.
metres long. Find its a) volume and b) surface area.
In the following exercises, find a) the volume and b) the surface area of the sphere with the given radius. Round answers to the nearest hundredth.
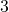 centimetres
centimetres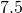 feet
feet
In the following exercises, solve. Round answers to the nearest hundredth.
- Exercise ball An exercise ball has a radius of
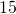 inches. Find its a) volume and b) surface area.
inches. Find its a) volume and b) surface area. - Golf ball A golf ball has a radius of
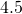 centimetres. Find its a) volume and b) surface area.
centimetres. Find its a) volume and b) surface area.
In the following exercises, write each number in scientific notation.
- 340,000
- 1,290,000
- 0.041
- 0.00000103
In the following exercises, convert each number to decimal form.
In the following exercises, multiply. Write your answer in decimal form.
In the following exercises, divide. Write your answer in decimal form.
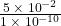
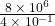
- The population of the world on July 1, 2010 was more than 6,850,000,000. Write the number in scientific notation
- The probability of winning the lottery was about 0.0000000057. Write the number in scientific notation.
- The width of a proton is
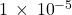 of the width of an atom. Convert this number to decimal form.
of the width of an atom. Convert this number to decimal form. - Coin production In 1942, the U.S. Mint produced 154,500,000 nickels. Write 154,500,000 in scientific notation.
-
Debt At the end of fiscal year 2019 the gross Canadian federal government debt was estimated to be approximately $685,450,000,000 ($685.45 billion), according to the Federal Budget. The population of Canada was approximately 37,590,000 people at the end of fiscal year 2019
a) Write the debt in scientific notation.
b) Write the population in scientific notation.
c) Find the amount of debt per person by using scientific notation to divide the debt by the population. Write the answer in scientific notation.
Answers:
-
- 243
- 9
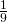
- 0.0016
-
- 64
- 14
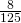
- 0.49
-
- 1296
- −1296
-
-
- −0.25
- 0.25
-
- 1
- 1
-
- 1
- −1
-
-
- 25
- 10000
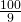
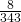
-
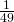
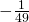
- 49
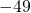
-
-
-
-
- 125 cu. cm
- 150 sq. cm
-
- 1124.864 cu. ft.
- 648.96 sq. ft
-
- 262,144 cu. ft
- 24,576 sq. ft
-
- 21.952 cu. m
- 47.04 sq. m
-
- 113.04 cu. cm
- 113.04 sq. cm
-
- 1,766.25 cu. ft
- 706.5 sq. ft
-
- 14,130 cu. in.
- 2,826 sq. in.
-
- 381.51 cu. cm
- 254.34 sq. cm
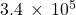
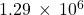
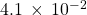
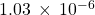
- 830
- 16,000,000,000
- 0.038
- 0.0000193
- 0.02
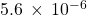
- 500,000,000
- 20,000,000
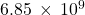
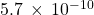
- 0.00001
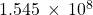
-
Attributions
This chapter has been adapted from “Integer Exponents and Scientific Notation” in Elementary Algebra (OpenStax) by Lynn Marecek and MaryAnne Anthony-Smith, which is under a CC BY 4.0 Licence. Adapted by Izabela Mazur. See the Copyright page for more information.

