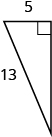5. Trigonometry
5.1 Use Properties of Angles, Triangles, and the Pythagorean Theorem
Learning Objectives
By the end of this section it is expected that you will be able to
- Use the properties of angles
- Use the properties of triangles
- Use the Pythagorean Theorem
Use the Properties of Angles
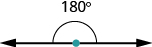
Are you familiar with the phrase ‘do a ![]() It means to make a full turn so that you face the opposite direction. It comes from the fact that the measure of an angle that makes a straight line is
It means to make a full turn so that you face the opposite direction. It comes from the fact that the measure of an angle that makes a straight line is ![]() degrees. See (Figure 1).
degrees. See (Figure 1).
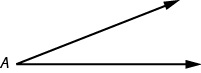
An angle is formed by two rays that share a common endpoint. Each ray is called a side of the angle and the common endpoint is called the vertex. An angle is named by its vertex. In (Figure 2), ![]() is the angle with vertex at point
is the angle with vertex at point ![]() . The measure of
. The measure of ![]() is written
is written ![]() .
.
We measure angles in degrees, and use the symbol ° to represent degrees. We use the abbreviation ![]() to for the measure of an angle. So if
to for the measure of an angle. So if ![]() is 27°, we would write
is 27°, we would write ![]() .
.
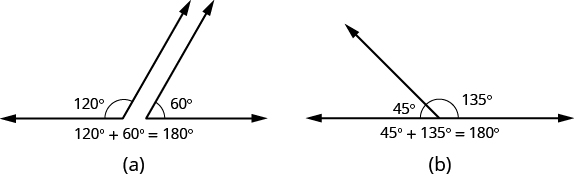
If the sum of the measures of two angles is ![]() °, then they are called supplementary angles. In (Figure 3), each pair of angles is supplementary because their measures add to
°, then they are called supplementary angles. In (Figure 3), each pair of angles is supplementary because their measures add to ![]() °. Each angle is the supplement of the other.
°. Each angle is the supplement of the other.
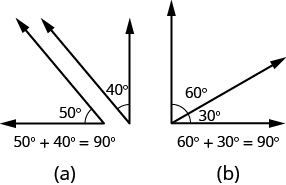
If the sum of the measures of two angles is ![]() °, then the angles are complementary angles. In (Figure 4), each pair of angles is complementary, because their measures add to
°, then the angles are complementary angles. In (Figure 4), each pair of angles is complementary, because their measures add to ![]() °. Each angle is the complement of the other.
°. Each angle is the complement of the other.
Supplementary and Complementary Angles
If the sum of the measures of two angles is ![]() °, then the angles are supplementary.
°, then the angles are supplementary.
If ![]() and
and ![]() are supplementary, then
are supplementary, then ![]() °.
°.
If the sum of the measures of two angles is ![]() °, then the angles are complementary.
°, then the angles are complementary.
If ![]() and
and ![]() are complementary, then
are complementary, then ![]() °.
°.
In this section and the next, you will be introduced to some common geometry formulas. We will adapt our Problem Solving Strategy for Geometry Applications. The geometry formula will name the variables and give us the equation to solve.
In addition, since these applications will all involve geometric shapes, it will be helpful to draw a figure and then label it with the information from the problem. We will include this step in the Problem Solving Strategy for Geometry Applications.
HOW TO: Use a Problem Solving Strategy for Geometry Applications
- Read the problem and make sure you understand all the words and ideas. Draw a figure and label it with the given information.
- Identify what you are looking for.
- Name what you are looking for and choose a variable to represent it.
- Translate into an equation by writing the appropriate formula or model for the situation. Substitute in the given information.
- Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
The next example will show how you can use the Problem Solving Strategy for Geometry Applications to answer questions about supplementary and complementary angles.
EXAMPLE 1
An angle measures ![]() °. Find a) its supplement, and b) its complement.
°. Find a) its supplement, and b) its complement.
| a) | |
| Step 1. Read the problem. Draw the figure and label it with the given information. | 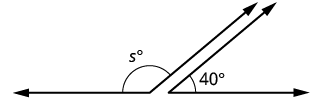 |
| Step 2. Identify what you are looking for. |  |
| Step 3. Name. Choose a variable to represent it. |  |
| Step 4. Translate. Write the appropriate formula for the situation and substitute in the given information. |
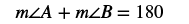 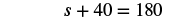 |
| Step 5. Solve the equation. |  |
Step 6. Check: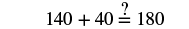 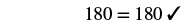 |
|
| Step 7. Answer the question. |  |
| b) | |
| Step 1. Read the problem. Draw the figure and label it with the given information. | 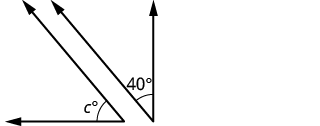 |
| Step 2. Identify what you are looking for. |  |
| Step 3. Name. Choose a variable to represent it. |  |
| Step 4. Translate. Write the appropriate formula for the situation and substitute in the given information. |
 |
| Step 5. Solve the equation. |   |
Step 6. Check: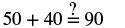 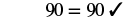 |
|
| Step 7. Answer the question. |  |
TRY IT 1
An angle measures ![]() °. Find its: a) supplement b) complement.
°. Find its: a) supplement b) complement.
Show answer
- 155°
- 65°
Did you notice that the words complementary and supplementary are in alphabetical order just like ![]() and
and ![]() are in numerical order?
are in numerical order?
EXAMPLE 2
Two angles are supplementary. The larger angle is ![]() ° more than the smaller angle. Find the measure of both angles.
° more than the smaller angle. Find the measure of both angles.
Solution
| Step 1. Read the problem. Draw the figure and label it with the given information. | 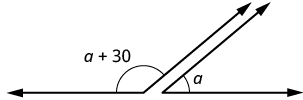 |
| Step 2. Identify what you are looking for. |  |
| Step 3. Name. Choose a variable to represent it. The larger angle is 30° more than the smaller angle. |
  |
| Step 4. Translate. Write the appropriate formula and substitute. |
 |
| Step 5. Solve the equation. |        |
Step 6. Check: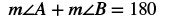 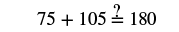 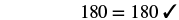 |
|
| Step 7. Answer the question. |  |
TRY IT 2
Two angles are supplementary. The larger angle is ![]() ° more than the smaller angle. Find the measures of both angles.
° more than the smaller angle. Find the measures of both angles.
Show answer
40°, 140°
Use the Properties of Triangles
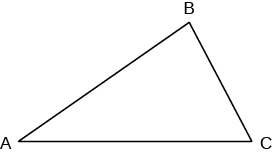
What do you already know about triangles? Triangle have three sides and three angles. Triangles are named by their vertices. The triangle in (Figure 5) is called ![]() , read ‘triangle
, read ‘triangle ![]() ’. We label each side with a lower case letter to match the upper case letter of the opposite vertex.
’. We label each side with a lower case letter to match the upper case letter of the opposite vertex.
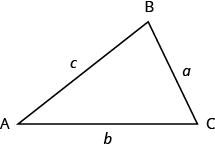
The three angles of a triangle are related in a special way. The sum of their measures is ![]() °.
°.
Sum of the Measures of the Angles of a Triangle
For any ![]() , the sum of the measures of the angles is
, the sum of the measures of the angles is ![]() °.
°.
EXAMPLE 3
The measures of two angles of a triangle are ![]() ° and
° and ![]() °. Find the measure of the third angle.
°. Find the measure of the third angle.
Solution
| Step 1. Read the problem. Draw the figure and label it with the given information. | 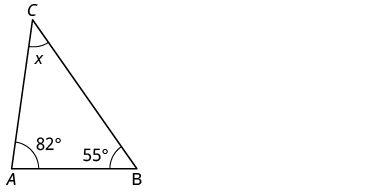 |
| Step 2. Identify what you are looking for. |  |
| Step 3. Name. Choose a variable to represent it. |  |
| Step 4. Translate. Write the appropriate formula and substitute. |
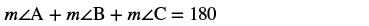 |
| Step 5. Solve the equation. | 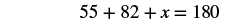 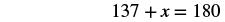  |
Step 6. Check: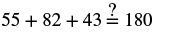 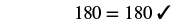 |
|
| Step 7. Answer the question. |  |
TRY IT 3
The measures of two angles of a triangle are ![]() ° and
° and ![]() °. Find the measure of the third angle.
°. Find the measure of the third angle.
Show answer
21°
Right Triangles
Some triangles have special names. We will look first at the right triangle. A right triangle has one ![]() ° angle, which is often marked with the symbol shown in (Figure 6).
° angle, which is often marked with the symbol shown in (Figure 6).
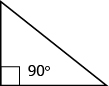
If we know that a triangle is a right triangle, we know that one angle measures ![]() ° so we only need the measure of one of the other angles in order to determine the measure of the third angle.
° so we only need the measure of one of the other angles in order to determine the measure of the third angle.
EXAMPLE 4
One angle of a right triangle measures ![]() °. What is the measure of the third angle?
°. What is the measure of the third angle?
Solution
| Step 1. Read the problem. Draw the figure and label it with the given information. | 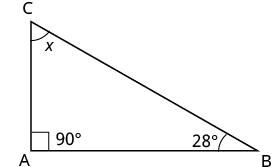 |
| Step 2. Identify what you are looking for. |  |
| Step 3. Name. Choose a variable to represent it. |  |
| Step 4. Translate. Write the appropriate formula and substitute. |
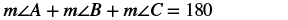 |
| Step 5. Solve the equation. | 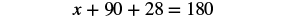 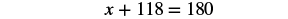  |
Step 6. Check: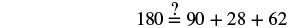 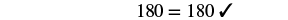 |
|
| Step 7. Answer the question. |  |
TRY IT 4
One angle of a right triangle measures ![]() °. What is the measure of the other angle?
°. What is the measure of the other angle?
Show answer
34°
In the examples so far, we could draw a figure and label it directly after reading the problem. In the next example, we will have to define one angle in terms of another. So we will wait to draw the figure until we write expressions for all the angles we are looking for.
EXAMPLE 5
The measure of one angle of a right triangle is ![]() ° more than the measure of the smallest angle. Find the measures of all three angles.
° more than the measure of the smallest angle. Find the measures of all three angles.
Solution
| Step 1. Read the problem. | |
| Step 2. Identify what you are looking for. | the measures of all three angles |
| Step 3. Name. Choose a variable to represent it.
Now draw the figure and label it with the given information. |
   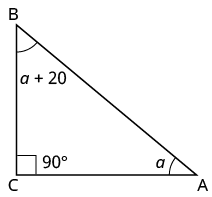 |
| Step 4. Translate. Write the appropriate formula and substitute into the formula. |
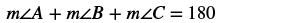 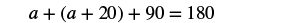 |
| Step 5. Solve the equation. | 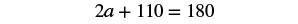 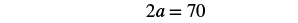 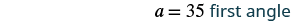     |
Step 6. Check: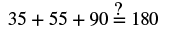  |
|
| Step 7. Answer the question. |  |
TRY IT 5
The measure of one angle of a right triangle is ![]() ° more than the measure of the smallest angle. Find the measures of all three angles.
° more than the measure of the smallest angle. Find the measures of all three angles.
Show answer
20°, 70°, 90°
Similar Triangles
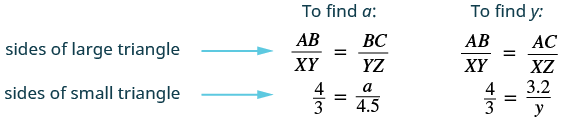
When we use a map to plan a trip, a sketch to build a bookcase, or a pattern to sew a dress, we are working with similar figures. In geometry, if two figures have exactly the same shape but different sizes, we say they are similar figures. One is a scale model of the other. The corresponding sides of the two figures have the same ratio, and all their corresponding angles are have the same measures.
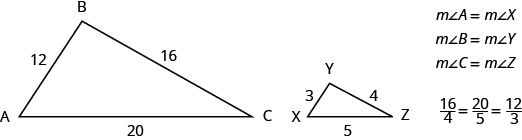
The two triangles in (Figure 7) are similar. Each side of ![]() is four times the length of the corresponding side of
is four times the length of the corresponding side of ![]() and their corresponding angles have equal measures.
and their corresponding angles have equal measures.
![]() and
and ![]() are similar triangles. Their corresponding sides have the same ratio and the corresponding angles have the same measure.
are similar triangles. Their corresponding sides have the same ratio and the corresponding angles have the same measure.
Properties of Similar Triangles
If two triangles are similar, then their corresponding angle measures are equal and their corresponding side lengths are in the same ratio.
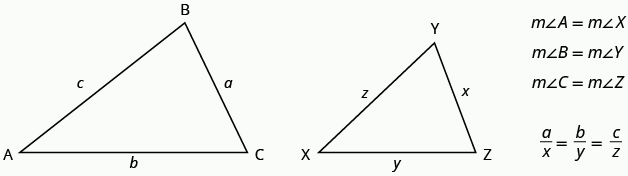
The length of a side of a triangle may be referred to by its endpoints, two vertices of the triangle. For example, in ![]()
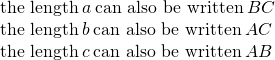
We will often use this notation when we solve similar triangles because it will help us match up the corresponding side lengths.
EXAMPLE 6
![]() and
and ![]() are similar triangles. The lengths of two sides of each triangle are shown. Find the lengths of the third side of each triangle.
are similar triangles. The lengths of two sides of each triangle are shown. Find the lengths of the third side of each triangle.
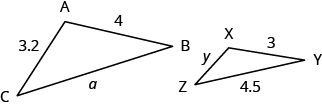
Solution
| Step 1. Read the problem. Draw the figure and label it with the given information. | The figure is provided. |
| Step 2. Identify what you are looking for. | The length of the sides of similar triangles |
| Step 3. Name. Choose a variable to represent it. | Let a = length of the third side of y = length of the third side |
| Step 4. Translate. | The triangles are similar, so the corresponding sides are in the same ratio. So Since the side Be careful to match up corresponding sides correctly.
|
| Step 5. Solve the equation. |
|
| Step 6. Check. |
 |
| Step 7. Answer the question. | The third side of |
TRY IT 6
![]() is similar to
is similar to ![]() . Find
. Find ![]() .
.
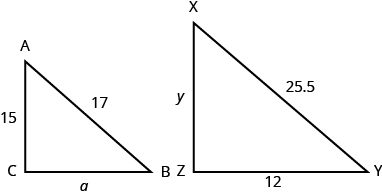
Show answer
8
Use the Pythagorean Theorem
The Pythagorean Theorem is a special property of right triangles that has been used since ancient times. It is named after the Greek philosopher and mathematician Pythagoras who lived around ![]() BCE.
BCE.
Remember that a right triangle has a ![]() ° angle, which we usually mark with a small square in the corner. The side of the triangle opposite the
° angle, which we usually mark with a small square in the corner. The side of the triangle opposite the ![]() ° angle is called the hypotenuse, and the other two sides are called the legs. See (Figure 8).
° angle is called the hypotenuse, and the other two sides are called the legs. See (Figure 8).
In a right triangle, the side opposite the ![]() ° angle is called the hypotenuse and each of the other sides is called a leg.
° angle is called the hypotenuse and each of the other sides is called a leg.
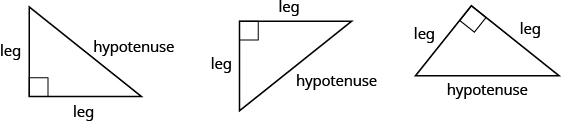
The Pythagorean Theorem tells how the lengths of the three sides of a right triangle relate to each other. It states that in any right triangle, the sum of the squares of the two legs equals the square of the hypotenuse.
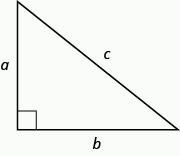
The Pythagorean Theorem
In any right triangle ![]() ,
,
where ![]() is the length of the hypotenuse
is the length of the hypotenuse ![]() and
and ![]() are the lengths of the legs.
are the lengths of the legs.
To solve problems that use the Pythagorean Theorem, we will need to find square roots. We defined the notation ![]() in this way:
in this way:
![]()
For example, we found that ![]() is
is ![]() because
because ![]() .
.
We will use this definition of square roots to solve for the length of a side in a right triangle.
EXAMPLE 7
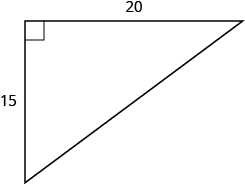
Use the Pythagorean Theorem to find the length of the hypotenuse.
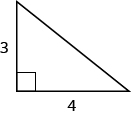
Solution
| Step 1. Read the problem. | |
| Step 2. Identify what you are looking for. | the length of the hypotenuse of the triangle |
| Step 3. Name. Choose a variable to represent it. | Let 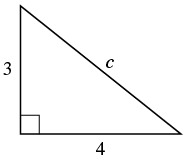 |
| Step 4. Translate. Write the appropriate formula. Substitute. |
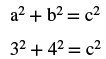 |
| Step 5. Solve the equation. | 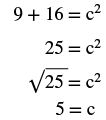 |
Step 6. Check: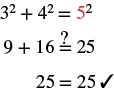 |
|
| Step 7. Answer the question. | The length of the hypotenuse is 5. |
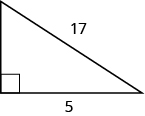
TRY IT 7
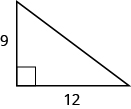
Use the Pythagorean Theorem to find the length of the hypotenuse.
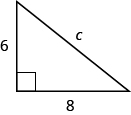
Show answer
10
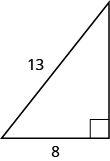
EXAMPLE 8
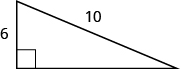
Use the Pythagorean Theorem to find the length of the longer leg.
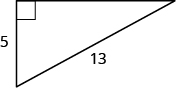
Solution
| Step 1. Read the problem. | |
| Step 2. Identify what you are looking for. | The length of the leg of the triangle |
| Step 3. Name. Choose a variable to represent it. | Let Label side b  |
| Step 4. Translate. Write the appropriate formula. Substitute. |
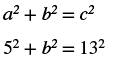 |
| Step 5. Solve the equation. Isolate the variable term. Use the definition of the square root. Simplify. |
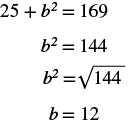 |
| Step 6. Check: | 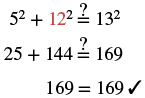 |
| Step 7. Answer the question. | The length of the leg is 12. |
TRY IT 8
Use the Pythagorean Theorem to find the length of the leg.
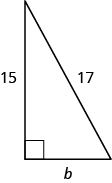
Show answer
8
EXAMPLE 9
Kelvin is building a gazebo and wants to brace each corner by placing a ![]() wooden bracket diagonally as shown. How far below the corner should he fasten the bracket if he wants the distances from the corner to each end of the bracket to be equal? Approximate to the nearest tenth of an inch.
wooden bracket diagonally as shown. How far below the corner should he fasten the bracket if he wants the distances from the corner to each end of the bracket to be equal? Approximate to the nearest tenth of an inch.
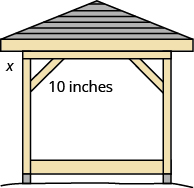
Solution
| Step 1. Read the problem. | |
| Step 2. Identify what you are looking for. | the distance from the corner that the bracket should be attached |
| Step 3. Name. Choose a variable to represent it. | Let x = the distance from the corner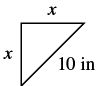 |
| Step 4. Translate. Write the appropriate formula. Substitute. |
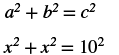 |
| Step 5. Solve the equation. Isolate the variable. Use the definition of the square root. Simplify. Approximate to the nearest tenth. |
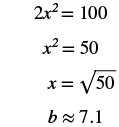 |
Step 6. Check: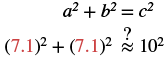 Yes. |
|
| Step 7. Answer the question. | Kelvin should fasten each piece of wood approximately 7.1″ from the corner. |
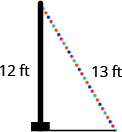
TRY IT 9
John puts the base of a ![]() ladder
ladder ![]() feet from the wall of his house. How far up the wall does the ladder reach?
feet from the wall of his house. How far up the wall does the ladder reach?

Show answer
12 feet
Key Concepts
- Supplementary and Complementary Angles
- If the sum of the measures of two angles is 180°, then the angles are supplementary.
- If
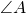 and
and 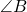 are supplementary, then
are supplementary, then 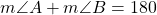 .
. - If the sum of the measures of two angles is 90°, then the angles are complementary.
- If
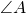 and
and 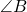 are complementary, then
are complementary, then 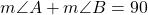 .
.
- Solve Geometry Applications
- Read the problem and make sure you understand all the words and ideas. Draw a figure and label it with the given information.
- Identify what you are looking for.
- Name what you are looking for and choose a variable to represent it.
- Translate into an equation by writing the appropriate formula or model for the situation. Substitute in the given information.
- Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
 Sum of the Measures of the Angles of a Triangle
Sum of the Measures of the Angles of a Triangle
- For any
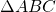 , the sum of the measures is 180°
, the sum of the measures is 180° 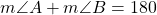
- For any
 Right Triangle
Right Triangle
- A right triangle is a triangle that has one 90° angle, which is often marked with a ⦜ symbol.
- Properties of Similar Triangles
- If two triangles are similar, then their corresponding angle measures are equal and their corresponding side lengths have the same ratio.
Glossary
- angle
- An angle is formed by two rays that share a common endpoint. Each ray is called a side of the angle.
- complementary angles
- If the sum of the measures of two angles is
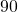 °, then they are called complementary angles.
°, then they are called complementary angles.
- hypotenuse
- The side of the triangle opposite the 90° angle is called the hypotenuse.
- legs of a right triangle
- The sides of a right triangle adjacent to the right angle are called the legs.
- right triangle
- A right triangle is a triangle that has one
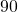 ° angle.
° angle.
- similar figures
- In geometry, if two figures have exactly the same shape but different sizes, we say they are similar figures.
- supplementary angles
- If the sum of the measures of two angles is
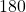 °, then they are called supplementary angles.
°, then they are called supplementary angles.
- triangle
- A triangle is a geometric figure with three sides and three angles.
- vertex of an angle
- When two rays meet to form an angle, the common endpoint is called the vertex of the angle.
5.1 Exercise Set
In the following exercises, find a) the supplement and b) the complement of the given angle.
- 53°
- 29°
In the following exercises, use the properties of angles to solve.
- Find the supplement of a 135° angle.
- Find the complement of a 27.5° angle.
- Two angles are supplementary. The larger angle is 56° more than the smaller angle. Find the measures of both angles.
- Two angles are complementary. The smaller angle is 34° less than the larger angle. Find the measures of both angles.
In the following exercises, solve using properties of triangles.
- The measures of two angles of a triangle are 26° and 98°. Find the measure of the third angle.
- The measures of two angles of a triangle are 105° and 31°. Find the measure of the third angle.
- One angle of a right triangle measures 33°. What is the measure of the other angle?
- One angle of a right triangle measures 22.5°. What is the measure of the other angle?
- The two smaller angles of a right triangle have equal measures. Find the measures of all three angles.
- The angles in a triangle are such that the measure of one angle is twice the measure of the smallest angle, while the measure of the third angle is three times the measure of the smallest angle. Find the measures of all three angles.
In the following exercises, ![]() is similar to
is similar to ![]() . Find the length of the indicated side.
. Find the length of the indicated side.
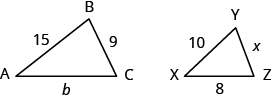
- side
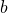
On a map, San Francisco, Las Vegas, and Los Angeles form a triangle whose sides are shown in the figure below. The actual distance from Los Angeles to Las Vegas is ![]() miles.
miles.
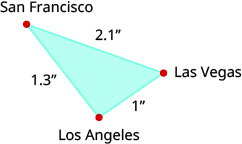
- Find the distance from Los Angeles to San Francisco.
In the following exercises, use the Pythagorean Theorem to find the length of the hypotenuse.
| 15.
|
16.
|
In the following exercises, use the Pythagorean Theorem to find the length of the missing side. Round to the nearest tenth, if necessary.
| 17.
|
18.
|
| 19.
|
20.
|
In the following exercises, solve. Approximate to the nearest tenth, if necessary.
|
21. A
|
22. Chi is planning to put a path of paving stones through her flower garden. The flower garden is a square with sides of
|
- Building a scale model Joe wants to build a doll house for his daughter. He wants the doll house to look just like his house. His house is
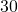 feet wide and
feet wide and 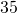 feet tall at the highest point of the roof. If the dollhouse will be
feet tall at the highest point of the roof. If the dollhouse will be 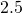 feet wide, how tall will its highest point be?
feet wide, how tall will its highest point be?
Answers:
-
- 127°
- 37°
-
- 151°
- 61°
- 45°
- 62.5°
- 62°, 118°
- 62°, 28°
- 56°
- 44°
- 57°
- 67.5°
- 45°, 45°, 90°
- 30°, 60°, 90°
- 12
- 351 miles
- 15
- 25
- 8
- 12
- 10.2
- 8
- 21.5 feet
- 14.1 feet
- 2.9 feet
Attributions:
This chapter has been adapted from “Use Properties of Angles, Triangles, and the Pythagorean Theorem” in Prealgebra (OpenStax) by Lynn Marecek, MaryAnne Anthony-Smith, and Andrea Honeycutt Mathis, which is under a CC BY 4.0 Licence. Adapted by Izabela Mazur. See the Adaptation Statement for more information.