Interest

Some people keep money at home in an easily accessible location, perhaps a piggy bank, a safe or locked box, or perhaps even a mattress. Although this provides instant access to funds it does not provide any return or earnings on this money. For that reason, most people hold their money in accounts or investments that provide some form of return or earning power.

Interest is the price paid for the use of money.  If you borrow money from another person or a lending institution, eventually you must pay back this amount plus the interest owing.  When you deposit money in a bank, you are lending them money and after some time they will pay you interest on the money you lent them.

The amount of interest you will owe or receive is determined by the principal,  the interest rate,  and the time (the length of the loan).  The amount of money that you lend or borrow is called the principal. The length of the loan can range between a few days to several years. The interest rate is stated as an annual percentage. It may be simple interest or compound interest. With simple interest the interest is calculated only once during the entire time period of the loan or deposit.  Simple interest is calculated solely on the principal investment or loan. With compound interest the interest is calculated more than once during the time period of the loan. It will be calculated on the principal as well as the accumulated interest This section will focus on simple interest and in the next section we will consider compound interest.

Simple Interest

Simple interest is calculated by finding the product of the principal (P), the rate (r), and the time (t).

Interest rates are quoted for periods of one year and when used in a formula must be converted to a decimal fraction. The time must be expressed in the same unit of time as the interest rate so time must be stated in years or portions of a year. If you deposit money in a savings account earning 3% interest then the annual interest rate is 3% per year.

EXAMPLE 1

Jo borrows $2000 at an interest rate of 5% per year.  How much interest will Jo owe after one year?

Solution

Identify the P, r, and t.     P = $2000     r = 5%  = 0.05      t = 1 year

Here,
			Replace P, r and t with their values
			Change 5% to its decimal equivalent, 0.05

Start with  the formula      I = Prt

I = 2000 (5%) (1)        Replace P, r, and t with their values

I = 2000 (0.05) (1)      Change 5% to its decimal equivalent, 0.05

I = 100

Jo will pay $100 in interest.

Note that the time t is expressed in terms of  years. When the time period is not exactly one year, the value for  t  will be the fraction of the year during which interest is earned.

If the investment is made for 3 months, then t = 3 months/12 months = 0.25 years.

If the investment is made for 35 days then  t = 35 days/365 days = 7/73 years.

EXAMPLE 3

Determine the interest that will be earned on  a deposit of $1350 at 2.8% over:

a) 7 months

b) 25 days

Solution:

a)

Interest of $22.05 over 7 months

b)

Interest of $2.59 over 25 days. Note that the answer is rounded to the nearest two decimal places or to the nearest cent.

EXAMPLE 4

Determine the interest that will be earned on  a deposit of $4200 at 4.65% over:

a) years

b) 5 weeks

Solution

a)

Interest of $292.95 over years

b)

Interest of $18.78 over 5 weeks. Note that the answer is rounded to the nearest two decimal places or to the nearest cent.

Maturity Value

The total amount of money due at the end of a loan period is called the maturity value of the loan. It is the amount to be paid on the due date of a loan or the amount to be paid to an investor at the end of the period for which an investment has been made.

In Example 1, Jo borrowed $2000 at an interest rate of 5%. At the end of one year Jo owed $100 in interest.

The maturity value of the loan is  MV = P + I  where  P = $2000 and I = $100.

MV = $2000 + $100 = $2100

The maturity value of the loan is $2100. At the end of the year Jo will be expected to pay back $2100.

EXAMPLE 5

Linda lends Ed $500.  Ed says he will pay her back in 60 days at 9% simple interest.  How much interest should Linda receive?  How much must Ed pay Linda altogether?

Solution

		Replace P, r and t with their values
		Multiply
		Round to the nearest cent

MV = P + I = $500 + $7.40 = $507.40

Linda should receive $7.40 in interest. At the end of 60 days Ed will owe Linda  $507.40.

Variations On Simple Interest

The amount of interest earned on an investment or due on a loan is calculated using I = Prt.

This formula can also be used to determine:

• the amount of principal (P) that needs to be invested in order to earn a certain amount of  interest over a certain period of time.
• the interest rate  (r)  that is needed in order to earn a certain amount of interest over a given time period.
• the amount of time (t) it will take in order to earn a certain amount of interest at a stated interest rate.

These amounts can be determined by solving the simple interest formula for any of  r, P or t.

Finding the Principal, Interest Rate, or Time

		where
To determine the principal use:		I = interest earned
To determine the interest rate use:		r = annual interest rate
To determine the time use:		P = principal
		t = time (in years)

The following memory aid is often called the “Magic Triangle”, because if you cover the variable you are trying to find, the formula will magically appear!

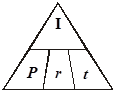
Determining the Principal

EXAMPLE  6

A six month investment will earn 5.25%.  How much would you need to invest if you want to earn $100 in interest?

Solution

The principal is unknown.  Cover P in the Magic Triangle.

P = ? or 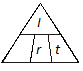 appears. Use the formula:

or		Replace I, r and t with their respective values
		Multiply 0.0525 by 0.5
		Divide 100 by 0.02625 and round answer to nearest cent

You would need to invest $3809.52

Determining the Interest Rate

EXAMPLE 7

Mariko had $240 in the bank for the month of April.  At the end of the month she had earned $0.90 in interest.  What interest rate was the bank paying?

Solution

The interest rate is unknown.  Cover r in the Magic Triangle.

r = ? or 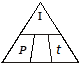appears. Use the formula:

t = 1 month =

Since r = 0.045, the interest rate as a percentage is 4.5%

Determining the Time

EXAMPLE 8

Carol invested $500 at an interest rate of  6%.  How long will it take her to earn $250 in interest?

Solution

The time is unknown.  Cover t in the Magic Triangle.

t = ? or 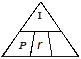appears. Use

r = 6% = 0.06
	or years

It will take 8.33 years.

When calculating time “t” using the simple interest formula, the answer will be in terms of years. Sometimes it is more reasonable to express the answer in terms of days or months.

Key Concepts

• to calculate the simple interest earned on an investment or charged on a loan we use the formula     I = Prt   where:

I = interest earned               r = annual interest rate ( stated as a decimal)

P = principal amount              t = time (in years)

• to determine the principal amount (P) for simple interest applications:
  • 
• to determine the time in years (t) for simple interest applications:
  • 
• to determine the interest rate (r) for simple interest applications:
  • 
• The Maturity Value (MV) of a loan is the sum of the principal P plus the interest I:

  MV = P + I

Glossary

9.1 Exercise Set

1. 1. How many days are in 1 year? If an investment is made for a period of  20 days, what portion of the year does this represent?
   2. How many weeks are in one year? If an investment is made for a period of  16 weeks, what portion of the year does this represent?
   3. How many months are in one year? If an investment is made for a period of  5 months, what portion of the year does this represent?
2. Calculate the simple interest earned for each of the following.
   

   a. $1000 at 10% for 1 year	b. $150 at 5% for 1 year
   c. $500 at 4.5% for 0.5 years	d. $200 at 11% for 3 months
   e. $100 at 7.25% for 6 months	f. $480 at 3.6% for 5 months
   g. $2500 at 6 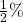for 100 days	h. $1800 at 5.25% for 30 weeks

3. 1. Mike borrowed $1500 from his mother. He agreed to pay her back in 9 months at 5%.
   2. How much in total will he owe her?
4. Mark won $10,000 and invested it for 32 weeks at 7.25% interest. a) How much interest did his investment earn? b) How much will he have in total at the end of the 32 weeks?
5. Barb invested $100. At the end of one year the investment had earned 16%. She then invested the whole amount (principal plus interest) and earned 12% in the second year.
   1. How much interest did Barb earn at the end of the first year?
   2. How much did she invest at the beginning of the second year?
   3. How much interest did she earn in the second year?
   4. How much did Barb have at the end of the two years?
6. Larry loaned Mary $2500 at 7%. Mary said she would pay Larry the $2500 plus interest in 90 days. What is the total amount of money that Mary should pay Larry in 90 days?
   1. 1. Find the principal needed to earn the following interest amounts:

7. a. $100 at 5% in 1 year	b. $15 at 2.5% in 18 weeks
   c. $60 at 9.5%  in 90 days	d. $1000 at 2.75% in 9 months

8. Find the interest rate (if necessary round final answers to the nearest hundredth) when:
   

   a. $1000 earns $25 in 1 year	b. $100 earns $3.60 in 5 months
   c. $4000 earns $10.60 in 13 weeks	d. $550 earns $4.80 in 73 days

   1. 1. . Find the time (if necessary round final answers to the nearest hundredth) needed to earn:

9. a. $5 interest on $100 at 10% (in months)	b. $1 interest on $1,000 at 12.5% (in days)
   c. $4 interest on $100 at 7.5%  (in days)	d. $3 interest on $100 at 10% (in months)

10. Fill in the missing values.
    

    I	P	r	t
    	$100.00	3%	1 year
    $50.00		5%	6 months
    $3.41	$630.00		1 month
    $9.50	$800.00	4.75%	months

11. At the beginning of the year, Bill invested $500 in a special account. At the end of the year the account was worth a total of $523.25. What interest rate did he earn on the $500 investment?
12. Velma invests $1200 at 6.5%.  How long (to the nearest  day) will it take to earn $10 in interest on the investment?
13. A short term lender charged $3.45 interest on a $230 purchase over a 30 day period. What interest rate did the lender charge?

Answers

1. 1. 365;  4/73
   2. 52;  2/13
   3. 12;   5/12
2. 1. $100
   2. $7.50
   3. $11.25
   4. $5.50
   5. $3.63
   6. $7.20
   7. $44.52
   8. $54.52
3. 1. interest $56.25
   2. $1500.00 + 56.25 = $1556.25
4. 1. I = $446.15
   2. $10446.15
5. 1. $16
   2. $116
   3. I = 116(0.12)(1) = $13.92
   4. $16.00 + $13.92 = $29.92
6. Mary owes Larry $2500 + $43.15 = $2543.15
7. 1. $2000.00
   2. $1733.33
   3. $2561.40
   4. $48 484.85
8. 1. 2.5%
   2. 8.64%
   3. 1.06%
   4. 4.36%
9. 1. 0.5 years = 6 month
   2. 0.008 years = 2.92 days
   3. 0.533 years = 194.67 days
   4. 0.3 years = 3.6 months

10. I	P	r	t
    $3.00	$100.00	3%	1 year
    $50.00	$2000.00	5%	6 months
    $3.41	$630.00	6.5%	1 month
    $38.00	$800.00	4.75%	3 months

11. 4.65%
12. 0.13 years or 47 days
13. 18.25%

Attribution

Some of the content for this chapter is from “Unit 1: Simple interest” and “Unit 2: Variations on simple interest” in Financial Mathematics by Paul Grinder, Velma McKay, Kim Moshenko, and Ada Sarsiat, which is under a CC BY 4.0 Licence.. Adapted by Kim Moshenko. See the Copyright page for more information.