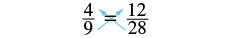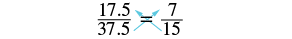6. Health Option
6.3 Proportions; Health Applications
Learning Objectives
By the end of this section it is expected that you will be able to:
- Use the definition of proportion
- Solve proportions
- Solve applications using proportions
- Write percent equations as proportions
- Translate and solve percent proportions
Use the Definition of Proportion
When two ratios or rates are equal, the equation relating them is called a proportion.
Proportion
A proportion is an equation of the form ![]() , where
, where ![]() .
.
The proportion states two ratios or rates are equal. The proportion is read ![]() is to
is to ![]() , as
, as ![]() is to
is to ![]()
The equation ![]() is a proportion because the two fractions are equal. The proportion
is a proportion because the two fractions are equal. The proportion ![]() is read
is read ![]() is to
is to ![]() as
as ![]() is to
is to ![]()
If we compare quantities with units, we have to be sure we are comparing them in the right order.
EXAMPLE 1
Write the sentence as a proportion:
72 heartbeats in 1 minute is the same as 216 heartbeats in 3 minutes.
| 72 is to 1 as 216 is to 3. | |
| Write as a proportion. | |
TRY IT 1
Write the sentence as a proportion:
![]() is to
is to ![]() as
as ![]() is to
is to ![]() .
.
Show answer
![]()
Look at the proportions ![]() and
and ![]() . From our work with equivalent fractions we know these equations are true. But how do we know if an equation is a proportion with equivalent fractions if it contains fractions with larger numbers?
. From our work with equivalent fractions we know these equations are true. But how do we know if an equation is a proportion with equivalent fractions if it contains fractions with larger numbers?
To determine if a proportion is true, we find the cross products of each proportion. To find the cross products, we multiply each denominator with the opposite numerator (diagonally across the equal sign). The results are called a cross products because of the cross formed. The cross products of a proportion are equal.

Cross Products of a Proportion
For any proportion of the form ![]() , where
, where ![]() , its cross products are equal.
, its cross products are equal.
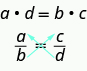
Cross products can be used to test whether a proportion is true. To test whether an equation makes a proportion, we find the cross products. If they are the equal, we have a proportion.
EXAMPLE 2
Determine whether each equation is a proportion:
To determine if the equation is a proportion, we find the cross products. If they are equal, the equation is a proportion.
| a) | |
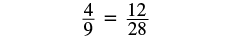 |
|
| Find the cross products. |
|
Since the cross products are not equal, ![]() , the equation is not a proportion.
, the equation is not a proportion.
| b) | |
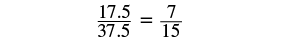 |
|
| Find the cross products. |
|
Since the cross products are equal, ![]() , the equation is a proportion.
, the equation is a proportion.
TRY IT 2
Determine whether each equation is a proportion:
Show answer
- no
- yes
Solve Proportions
To solve a proportion containing a variable, we remember that the proportion is an equation. All of the techniques we have used so far to solve equations still apply. In the next example, we will solve a proportion by multiplying by the Least Common Denominator (LCD) using the Multiplication Property of Equality.
EXAMPLE 3
Solve: ![]() .
.
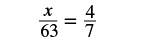 |
|
| To isolate |
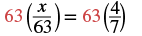 |
| Simplify. | 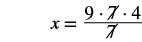 |
| Divide the common factors. | 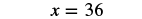 |
| Check: To check our answer, we substitute into the original proportion. | |
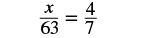 |
|
 |
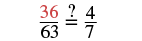 |
| Show common factors. | 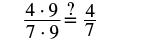 |
| Simplify. | 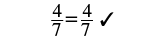 |
TRY IT 3
Solve the proportion: ![]() .
.
Show answer
77
When the variable is in a denominator, we’ll use the fact that the cross products of a proportion are equal to solve the proportions.
We can find the cross products of the proportion and then set them equal. Then we solve the resulting equation using our familiar techniques.
EXAMPLE 4
Solve: ![]() .
.
Notice that the variable is in the denominator, so we will solve by finding the cross products and setting them equal.
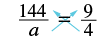 |
||
| Find the cross products and set them equal. | 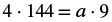 |
|
| Simplify. | 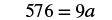 |
|
| Divide both sides by 9. | 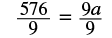 |
|
| Simplify. | 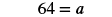 |
|
| Check your answer: | ||
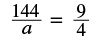 |
||
| Substitute a = 64 | 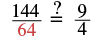 |
|
| Show common factors. | 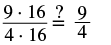 |
|
| Simplify. | 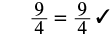 |
|
Another method to solve this would be to multiply both sides by the LCD, ![]() . Try it and verify that you get the same solution.
. Try it and verify that you get the same solution.
TRY IT 4
Solve the proportion: ![]() .
.
Show answer
65
EXAMPLE 5
Solve: ![]() .
.
| Find the cross products and set them equal. | 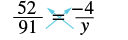 |
|
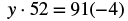 |
||
| Simplify. | 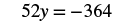 |
|
| Divide both sides by 52. | 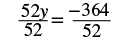 |
|
| Simplify. | 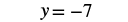 |
|
| Check: | ||
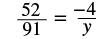 |
||
| Substitute y = −7 |
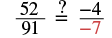 |
|
| Show common factors. | 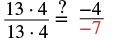 |
|
| Simplify. | 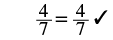 |
|
TRY IT 5
Solve the proportion: ![]() .
.
Show answer
−7
Solve Applications Using Proportions
When we set up the proportion, we must make sure the units are correct—the units in the numerators match and the units in the denominators match.
EXAMPLE 6
When pediatricians prescribe acetaminophen to children, they prescribe ![]() millilitres (ml) of acetaminophen for every
millilitres (ml) of acetaminophen for every ![]() pounds of the child’s weight. If Zoe weighs
pounds of the child’s weight. If Zoe weighs ![]() pounds, how many millilitres of acetaminophen will her doctor prescribe?
pounds, how many millilitres of acetaminophen will her doctor prescribe?
| Identify what you are asked to find. | How many ml of acetaminophen the doctor will prescribe |
| Choose a variable to represent it. | Let |
| Write a sentence that gives the information to find it. | If 5 ml is prescribed for every 25 pounds, how much will be prescribed for 80 pounds? |
| Translate into a proportion. | 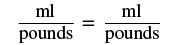 |
| Substitute given values—be careful of the units. | 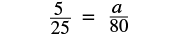 |
| Multiply both sides by 80. | 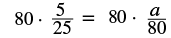 |
| Multiply and show common factors. | 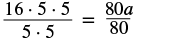 |
| Simplify. | 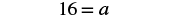 |
| Check if the answer is reasonable. | |
| Yes. Since 80 is about 3 times 25, the medicine should be about 3 times 5. | |
| Write a complete sentence. | The pediatrician would prescribe 16 ml of acetaminophen to Zoe. |
You could also solve this proportion by setting the cross products equal.
TRY IT 6
Pediatricians prescribe ![]() millilitres (ml) of acetaminophen for every
millilitres (ml) of acetaminophen for every ![]() pounds of a child’s weight. How many millilitres of acetaminophen will the doctor prescribe for Emilia, who weighs
pounds of a child’s weight. How many millilitres of acetaminophen will the doctor prescribe for Emilia, who weighs ![]() pounds?
pounds?
Show answer
12 ml
EXAMPLE 7
The doctor prescribes for you to take 60 milligrams of the medication that is found in a liquid cough syrup. The label on the syrup reads 100 mg /5 mL. How much cough syrup should you take?
| Identify what you are asked to find. | How much cough syrup you should take? |
| Choose a variable to represent it. | Let |
| Write a sentence that gives the information to find it. | If there is 100 mg in 5 mL, then 60 mg is in what amount? |
| Translate into a proportion. | |
| Substitute given values. | |
| Use the cross product. | |
| Divide by 100. | x = 3 |
| Check if the answer is reasonable. | |
| Yes. Since 60 mg is less then 100 mg, than 3 mL is less that 5 mL. | |
| Write a complete sentence. | You should take 3 mL of cough syrup. |
TRY IT 7
The doctor prescribes 30 milligrams of the medication found in the liquid cough syrup to your daughter. The label on the syrup reads 100 mg /5 mL. How much cough syrup you should give to your daughter?
Show answer
1.5 mL
EXAMPLE 8
For adults over 18, the recommended daily allowance for protein is 0.8 grams per 1 kilogram of body weight. How many grams of protein is an adult allowed to consume per day if your weight is 68 kilograms?
| Identify what you are asked to find. | How many grams of protein is an adult allowed to consume per day? |
| Choose a variable to represent it. | Let |
| Write a sentence that gives the information to find it. | If 0.8 gr is allowed for 1 kg, then how many grams is allowed for 68 kg? |
| Translate into a proportion. | |
| Substitute given values. | |
| The variable is in the denominator, so find the cross products and set them equal. | |
| Simplify. | p = 54.4 |
| Check if the answer is reasonable. | |
| Yes, if the allowance would be 1 gram per 1 kilogram, it would be 68 grams a day. | |
| Write a complete sentence. | An adult over 18 is allowed to consume 54.4 grams of protein. |
TRY IT 8
Base on example 8, how many grams of protein is Nicole allowed if her weight is 52 kilograms?
Show answer
41.6 grams
Write Percent Equations As Proportions
The proportion method for solving percent problems involves a percent proportion. A percent proportion is an equation where a percent is equal to an equivalent ratio.
For example, ![]() and we can simplify
and we can simplify ![]() . Since the equation
. Since the equation ![]() shows a percent equal to an equivalent ratio, we call it a percent proportion. Using the vocabulary we used earlier:
shows a percent equal to an equivalent ratio, we call it a percent proportion. Using the vocabulary we used earlier:
![]()
Percent Proportion
The amount is to the base as the percent is to ![]() .
.
![]()
If we restate the problem in the words of a proportion, it may be easier to set up the proportion:
![]()
We could also say:
![]()
First we will practice translating into a percent proportion. Later, we’ll solve the proportion.
EXAMPLE 9
Translate to a proportion. What number is ![]() of
of ![]()
If you look for the word “of”, it may help you identify the base.
| Identify the parts of the percent proportion. |  |
| Restate as a proportion. |  |
| Set up the proportion. Let |
TRY IT 9
Translate to a proportion: What number is ![]() of
of ![]()
Show answer
![]()
EXAMPLE 10
Translate to a proportion. ![]() is
is ![]() of what number?
of what number?
| Identify the parts of the percent proportion. |  |
| Restate as a proportion. |  |
| Set up the proportion. Let |
TRY IT 10
Translate to a proportion: ![]() is
is ![]() of what number?
of what number?
Show answer
![]()
EXAMPLE 11
Translate to a proportion. What percent of ![]() is
is ![]()
| Identify the parts of the percent proportion. |  |
| Restate as a proportion. |  |
| Set up the proportion. Let |
TRY IT 11
Translate to a proportion: What percent of ![]() is
is ![]()
Show answer
![]()
Translate and Solve Percent Proportions
Now that we have written percent equations as proportions, we are ready to solve the equations.
EXAMPLE 12
A human body is made up of mostly water. As we age, total body water content also diminishes so that by the time we are in our eighties the percent of water in our bodies has decreased to around 45%. If your grandfather weights 80 kg, what number is the 45% of his weight?
| Identify the parts of the percent proportion. |  |
| Restate as a proportion. |  |
| Set up the proportion. Let |
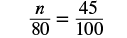 |
| Find the cross products and set them equal. | 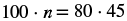 |
| Simplify. | 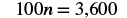 |
| Divide both sides by 100. | 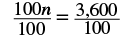 |
| Simplify. | 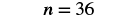 |
| Check if the answer is reasonable. | |
| Yes. 45 is a little less than half of 100 and 36 is a little less than half 80. | |
| Write a complete sentence that answers the question. | 36 kg is 45% of 80 kg. |
TRY IT 12
Adult male typically are composed of about 60% water. If a male weights 86 kg, what number is ![]() of
of ![]()
Show answer
51.6 kg
In the next example, the percent is more than ![]() , which is more than one whole. So the unknown number will be more than the base.
, which is more than one whole. So the unknown number will be more than the base.
EXAMPLE 13
According to Wikipedia, the red blood cells of an average adult human male store collectively about 2.5 grams of iron. This represents 65% of the total iron contained in the body. Find the total amount of iron contained in the body. Round your answer to the nearest tenth.
| Identify the parts of the percent proportion. | 65% = percent, 2.5 grams = amount, base = ? |
| Restate as a proportion. | 65% of what number is 2.5 |
| Set up the proportion. Let |
|
| Find the cross products and set them equal. | |
| Simplify. | 65 n = 250 |
| Divide both sides by 65. | |
| Simplify. | n = 3.8 |
| Check if the answer is reasonable. | |
| Yes.100% is more than 65% and 3.8 is more than 2.5. | |
| Write a complete sentence that answers the question. | The total amount of iron in the body of an average adult human male is 3.8 grams. |
TRY IT 13
Translate and solve using proportions: ![]() of
of ![]() is what number?
is what number?
Show answer
44.8
EXAMPLE 14
The daily recommended intake for potassium is 4700 grams. If a medium sized banana contains 425 grams of potassium, what percent of the daily recommended intake is that? Round to one decimal place.
| Identify the parts of the percent proportion. | 4700 = base, 425 = amount, percent = ? |
| Restate as a proportion. | What percent of 4700 is 425? |
| Set up the proportion. Let |
|
| Find the cross products and set them equal. | |
| Simplify. | 4700 n = 42500 |
| Divide both sides by 4700. | |
| Simplify. | n = 9 |
| Check if the answer is reasonable. | |
| Yes. 9 is less than 10 and 425 is less than 470. | |
| Write a complete sentence that answers the question. | 425 is 9% of 4700. |
TRY IT 14
Translate and solve using proportions: What percent of ![]() is
is ![]()
Show answer
37.5%
Key Concepts
- Proportion
- A proportion is an equation of the form
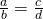 , where
, where 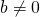 ,
, 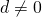 .The proportion states two ratios or rates are equal. The proportion is read “
.The proportion states two ratios or rates are equal. The proportion is read “ is to
is to 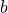 , as
, as  is to
is to 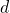 ”.
”.
- A proportion is an equation of the form
- Cross Products of a Proportion
- For any proportion of the form
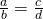 , where
, where 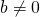 , its cross products are equal:
, its cross products are equal: 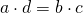 .
.
- For any proportion of the form
- Percent Proportion
- The amount is to the base as the percent is to 100.
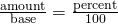
- The amount is to the base as the percent is to 100.
Glossary
- proportion
- A proportion is an equation of the form
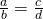 , where
, where 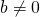 ,
, 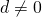 .The proportion states two ratios or rates are equal. The proportion is read “
.The proportion states two ratios or rates are equal. The proportion is read “ is to
is to 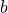 , as
, as  is to
is to 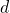 ”.
”.
6.3 Exercise Set
In the following exercises, write each sentence as a proportion.
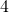 is to
is to 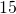 as
as 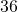 is to
is to 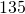 .
.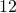 is to
is to 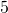 as
as 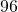 is to
is to 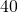 .
.
In the following exercises, determine whether each equation is a proportion.
In the following exercises, solve each proportion.
In the following exercises, solve the proportion problem.
- Pediatricians prescribe
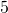 millilitre s (ml) of acetaminophen for every
millilitre s (ml) of acetaminophen for every 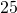 pounds of a child’s weight. How many millilitres of acetaminophen will the doctor prescribe for Jocelyn, who weighs
pounds of a child’s weight. How many millilitres of acetaminophen will the doctor prescribe for Jocelyn, who weighs 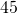 pounds?
pounds? - At the gym, Carol takes her pulse for
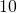 sec and counts
sec and counts 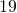 beats. How many beats per minute is this? Has Carol met her target heart rate of
beats. How many beats per minute is this? Has Carol met her target heart rate of 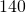 beats per minute?
beats per minute? - A new energy drink advertises
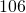 calories for
calories for 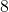 ounces. How many calories are in
ounces. How many calories are in 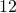 ounces of the drink?
ounces of the drink? - Karen eats
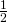 cup of oatmeal that counts for
cup of oatmeal that counts for 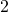 points on her weight loss program. Her husband, Joe, can have
points on her weight loss program. Her husband, Joe, can have 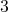 points of oatmeal for breakfast. How much oatmeal can he have?
points of oatmeal for breakfast. How much oatmeal can he have? - Brianna, who weighs
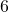 kg, just received her shots and needs a pain killer. The pain killer is prescribed for children at
kg, just received her shots and needs a pain killer. The pain killer is prescribed for children at 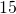 milligrams (mg) for every
milligrams (mg) for every 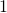 kilogram (kg) of the child’s weight. How many milligrams will the doctor prescribe?
kilogram (kg) of the child’s weight. How many milligrams will the doctor prescribe? - Kevin wants to keep his heart rate at
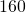 beats per minute while training. During his workout he counts
beats per minute while training. During his workout he counts 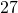 beats in
beats in 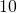 seconds. How many beats per minute is this? Has Kevin met his target
seconds. How many beats per minute is this? Has Kevin met his target - One brand of microwave popcorn has
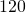 calories per serving. A whole bag of this popcorn has
calories per serving. A whole bag of this popcorn has 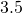 servings. How many calories are in a whole bag of this microwave popcorn?
servings. How many calories are in a whole bag of this microwave popcorn? - Marissa loves the Caramel Macchiato at the coffee shop. The
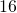 oz. medium size has
oz. medium size has 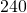 calories. How many calories will she get if she drinks the large
calories. How many calories will she get if she drinks the large 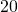 oz. size?
oz. size? - For every
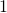 kilogram (kg) of a child’s weight, pediatricians prescribe
kilogram (kg) of a child’s weight, pediatricians prescribe 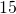 milligrams (mg) of a fever reducer. If Isabella weighs
milligrams (mg) of a fever reducer. If Isabella weighs 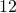 kg, how many milligrams of the fever reducer will the pediatrician prescribe?
kg, how many milligrams of the fever reducer will the pediatrician prescribe?
In the following exercises, translate to a proportion.
- What number is
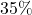 of
of 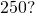
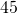 is
is 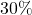 of what number?
of what number?- What percent of
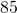 is
is 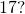
In the following exercises, translate and solve using proportions.
- What number is
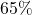 of
of 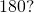
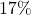 of what number is
of what number is 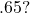
- What percent of
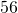 is
is 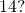
Answers
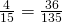
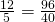
- yes
- no
- no
- yes
- 49
- 47
- 9
- -11
- 7
- 2
- 0.6
- 14.4
- 9 ml
- 114, no
- 159 cal
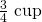
- 90 mg
- 162, no
- 420 cal
- 300 cal
- 180 mg
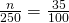
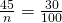
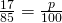
- 117
- 45
- 25%
Attributions
- This chapter has been adapted from “Solve Proportions and their Applications” in Prealgebra (OpenStax) by Lynn Marecek, MaryAnne Anthony-Smith, and Andrea Honeycutt Mathis, which is under a CC BY 4.0 Licence. Adapted by Izabela Mazur. See the Copyright page for more information.
- OER.hawaii.edu
- Wikipedia
- Government of Canada Statistics