1. Operations with Real Numbers
1.4 Decimals
Learning Objectives
By the end of this section it is expected that you will be able to:
- Round decimals
- Add and subtract decimals
- Multiply and divide decimals
- Convert decimals, fractions, and percent
Decimals are another way of writing fractions whose denominators are powers of 10.
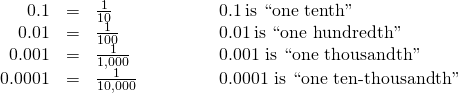
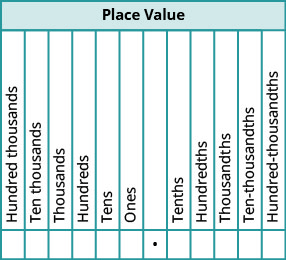
Notice that “ten thousand” is a number larger than one, but “one ten-thousandth” is a number smaller than one. The “th” at the end of the name tells you that the number is smaller than one.
When we name a whole number, the name corresponds to the place value based on the powers of ten. We read 10,000 as “ten thousand” and 10,000,000 as “ten million.” Likewise, the names of the decimal places correspond to their fraction values. Figure 1 shows the names of the place values to the left and right of the decimal point.
Round Decimals
Rounding decimals is very much like rounding whole numbers. We will round decimals with a method based on the one we used to round whole numbers.
EXAMPLE 1




TRY IT 1
Round to the nearest hundredth: ![]() .
.
Show answer
1.05
We summarize the steps for rounding a decimal here.
HOW TO: Round Decimals
- Locate the given place value and mark it with an arrow.
- Underline the digit to the right of the place value.
- Is this digit greater than or equal to 5?
- Yes—add 1 to the digit in the given place value.
- No—do not change the digit in the given place value.
- Rewrite the number, deleting all digits to the right of the rounding digit.
EXAMPLE 2
Round 18.379 to the nearest a) tenth b) whole number.
Round 18.379
a) to the nearest tenth
| Locate the tenths place with an arrow. |  |
| Underline the digit to the right of the given place value. |  |
| Because 7 is greater than or equal to 5, add 1 to the 3. |  |
| Rewrite the number, deleting all digits to the right of the rounding digit. | 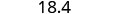 |
| Notice that the deleted digits were NOT replaced with zeros. | So, 18.379 rounded to the nearest tenth is 18.4. |
b) to the nearest whole number
| Locate the ones place with an arrow. |  |
| Underline the digit to the right of the given place value. | 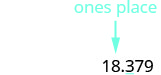 |
| Since 3 is not greater than or equal to 5, do not add 1 to the 8. |  |
| Rewrite the number, deleting all digits to the right of the rounding digit. |  |
| So, 18.379 rounded to the nearest whole number is 18. |
TRY IT 2
Round ![]() to the nearest a) hundredth b) tenth c) whole number.
to the nearest a) hundredth b) tenth c) whole number.
Show answer
a) 6.58 b) 6.6 c) 7
Add and Subtract Decimals
To add or subtract decimals, we line up the decimal points. By lining up the decimal points this way, we can add or subtract the corresponding place values. We then add or subtract the numbers as if they were whole numbers and then place the decimal point in the sum.
HOW TO: Add or Subtract Decimals
- Write the numbers so the decimal points line up vertically.
- Use zeros as place holders, as needed.
- Add or subtract the numbers as if they were whole numbers. Then place the decimal point in the answer under the decimal points in the given numbers.
EXAMPLE 3
Add: ![]() .
.
| Write the numbers so the decimal points line up vertically. | |
| Put 0 as a placeholder after the 5 in 23.5. Remember, |
|
| Add the numbers as if they were whole numbers. Then place the decimal point in the sum. |
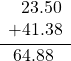 |
TRY IT 3
Add: ![]() .
.
Show answer
16.49
EXAMPLE 4
Subtract: ![]() .
.
| Write the numbers so the decimal points line up vertically. Remember, 20 is a whole number, so place the decimal point after the 0. |
|
| Put in zeros to the right as placeholders. | |
| Subtract and place the decimal point in the answer. | 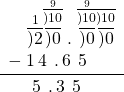 |
TRY IT 4
Subtract: ![]() .
.
Show answer
0.42
Multiply and Divide Decimals
Multiplying decimals is very much like multiplying whole numbers—we just have to determine where to place the decimal point. The procedure for multiplying decimals will make sense if we first convert them to fractions and then multiply.
So let’s see what we would get as the product of decimals by converting them to fractions first. We will do two examples side-by-side. Look for a pattern!
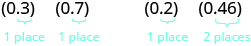 |
|
| Convert to fractions. |
 |
| Multiply. |  |
| Convert to decimals. |  |
Notice, in the first example, we multiplied two numbers that each had one digit after the decimal point and the product had two decimal places. In the second example, we multiplied a number with one decimal place by a number with two decimal places and the product had three decimal places.
We multiply the numbers just as we do whole numbers, temporarily ignoring the decimal point. We then count the number of decimal points in the factors and that sum tells us the number of decimal places in the product.
The rules for multiplying positive and negative numbers apply to decimals, too, of course!
When multiplying two numbers,
- if their signs are the same the product is positive.
- if their signs are different the product is negative.
When we multiply signed decimals, first we determine the sign of the product and then multiply as if the numbers were both positive. Finally, we write the product with the appropriate sign.
HOW TO: Multiply Decimals
- Determine the sign of the product.
- Write in vertical format, lining up the numbers on the right. Multiply the numbers as if they were whole numbers, temporarily ignoring the decimal points.
- Place the decimal point. The number of decimal places in the product is the sum of the number of decimal places in the factors.
- Write the product with the appropriate sign.
EXAMPLE 5
Multiply: ![]() .
.
| (−3.9)(4.075) | |
| The signs are different. The product will be negative. | |
| Write in vertical format, lining up the numbers on the right. | 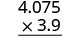 |
| Multiply. | 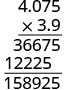 |
| Add the number of decimal places in the factors (1 + 3).
|
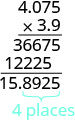 |
| The signs are different, so the product is negative. | (−3.9)(4.075) = −15.8925 |
TRY IT 5
Multiply: ![]() .
.
Show answer
![]()
In many of your other classes, especially in the sciences, you will multiply decimals by powers of 10 (10, 100, 1000, etc.). If you multiply a few products on paper, you may notice a pattern relating the number of zeros in the power of 10 to number of decimal places we move the decimal point to the right to get the product.
HOW TO: Multiply a Decimal by a Power of Ten
- Move the decimal point to the right the same number of places as the number of zeros in the power of 10.
- Add zeros at the end of the number as needed.
EXAMPLE 6
Multiply 5.63 a) by 10 b) by 100 c) by 1,000.
By looking at the number of zeros in the multiple of ten, we see the number of places we need to move the decimal to the right.
a)
| 5.63(10) | |
| There is 1 zero in 10, so move the decimal point 1 place to the right. |  |
b)
| 5.63(100) | |
| There are 2 zeros in 100, so move the decimal point 2 places to the right. |  |
c)
| 5.63(1,000) | |
| There are 3 zeros in 1,000, so move the decimal point 3 places to the right. | 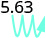 |
| A zero must be added at the end. | 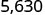 |
TRY IT 6
Multiply 2.58 a) by 10 b) by 100 c) by 1,000.
Show answer
a) 25.8 b) 258 c) 2,580
Just as with multiplication, division of decimals is very much like dividing whole numbers. We just have to figure out where the decimal point must be placed.
To divide decimals, determine what power of 10 to multiply the denominator by to make it a whole number. Then multiply the numerator by that same power of ![]() . Because of the equivalent fractions property, we haven’t changed the value of the fraction! The effect is to move the decimal points in the numerator and denominator the same number of places to the right. For example:
. Because of the equivalent fractions property, we haven’t changed the value of the fraction! The effect is to move the decimal points in the numerator and denominator the same number of places to the right. For example:
![]()
We use the rules for dividing positive and negative numbers with decimals, too. When dividing signed decimals, first determine the sign of the quotient and then divide as if the numbers were both positive. Finally, write the quotient with the appropriate sign.
We review the notation and vocabulary for division:
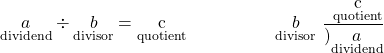
We’ll write the steps to take when dividing decimals, for easy reference.
HOW TO: Divide Decimals
- Determine the sign of the quotient.
- Make the divisor a whole number by “moving” the decimal point all the way to the right. “Move” the decimal point in the dividend the same number of places—adding zeros as needed.
- Divide. Place the decimal point in the quotient above the decimal point in the dividend.
- Write the quotient with the appropriate sign.
EXAMPLE 7
Divide: ![]() .
.
Remember, you can “move” the decimals in the divisor and dividend because of the Equivalent Fractions Property.
| The signs are the same. | The quotient is positive. |
| Make the divisor a whole number by “moving” the decimal point all the way to the right. | |
| “Move” the decimal point in the dividend the same number of places. | 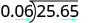 |
| Divide. Place the decimal point in the quotient above the decimal point in the dividend. |
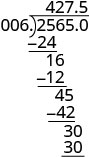 |
| Write the quotient with the appropriate sign. |
TRY IT 7
Divide: ![]() .
.
Show answer
587.3
A common application of dividing whole numbers into decimals is when we want to find the price of one item that is sold as part of a multi-pack. For example, suppose a case of 24 water bottles costs $3.99. To find the price of one water bottle, we would divide $3.99 by 24. We show this division in the next example. In calculations with money, we will round the answer to the nearest cent (hundredth).
EXAMPLE 8
Divide: ![]() .
.
| Place the decimal point in the quotient above the decimal point in the dividend. | |
| Divide as usual. When do we stop? Since this division involves money, we round it to the nearest cent (hundredth.) To do this, we must carry the division to the thousandths place. |
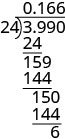 |
| Round to the nearest cent. |
TRY IT 8
Divide: ![]() .
.
Show answer
$0.19
Convert Decimals and Fractions
We convert decimals into fractions by identifying the place value of the last (farthest right) digit. In the decimal 0.03 the 3 is in the hundredths place, so 100 is the denominator of the fraction equivalent to 0.03
![]()
Notice, when the number to the left of the decimal is zero, we get a fraction whose numerator is less than its denominator. Fractions like this are called proper fractions.
The steps to take to convert a decimal to a fraction are summarized in the procedure box.
HOW TO: Covert a Decimal to a Proper Fraction
- Determine the place value of the final digit.
- Write the fraction.
- numerator—the “numbers” to the right of the decimal point
- denominator—the place value corresponding to the final digit
EXAMPLE 9
Write 0.374 as a fraction.
| Determine the place value of the final digit. |  |
Write the fraction for 0.374:
|
|
| Simplify the fraction. | |
| Divide out the common factors. | so, |
Did you notice that the number of zeros in the denominator of ![]() is the same as the number of decimal places in 0.374?
is the same as the number of decimal places in 0.374?
TRY IT 9
Write 0.234 as a fraction.
Show answer
![]()
We’ve learned to convert decimals to fractions. Now we will do the reverse—convert fractions to decimals. Remember that the fraction bar means division. So ![]() can be written
can be written ![]() or
or ![]() . This leads to the following method for converting a fraction to a decimal.
. This leads to the following method for converting a fraction to a decimal.
HOW TO: Covert a Fraction to a Decimal
To convert a fraction to a decimal, divide the numerator of the fraction by the denominator of the fraction.
EXAMPLE 10
Write ![]() as a decimal.
as a decimal.
Since a fraction bar means division, we begin by writing ![]() as
as ![]() . Now divide.
. Now divide.

TRY IT 10
Write ![]() as a decimal.
as a decimal.
Show answer
![]()
When we divide, we will not always get a zero remainder. Sometimes the quotient ends up with a decimal that repeats. A repeating decimal is a decimal in which the last digit or group of digits repeats endlessly. A bar is placed over the repeating block of digits to indicate it repeats.
Repeating Decimal
A repeating decimal is a decimal in which the last digit or group of digits repeats endlessly.
A bar is placed over the repeating block of digits to indicate it repeats.
EXAMPLE 11
Write ![]() as a decimal.
as a decimal.
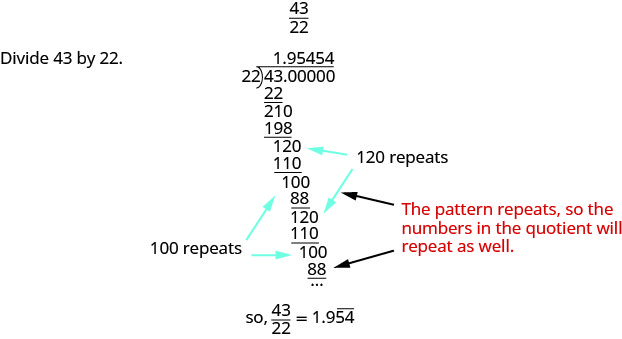
TRY IT 11
Write ![]() as a decimal.
as a decimal.
Show answer
![]()
Sometimes we may have to simplify expressions with fractions and decimals together.
EXAMPLE 12
Simplify: ![]() .
.
First we must change one number so both numbers are in the same form. We can change the fraction to a decimal, or change the decimal to a fraction. Usually it is easier to change the fraction to a decimal.
| Change |
 |
|
| Add. | ||
| So, |
TRY IT 12
Simplify: ![]() .
.
Show answer
5.275
Key Concepts
- Round a Decimal
- Locate the given place value and mark it with an arrow.
- Underline the digit to the right of the place value.
- Is this digit greater than or equal to 5? Yes—add 1 to the digit in the given place value. No—do not change the digit in the given place value.
- Rewrite the number, deleting all digits to the right of the rounding digit.
- Add or Subtract Decimals
- Write the numbers so the decimal points line up vertically.
- Use zeros as place holders, as needed.
- Add or subtract the numbers as if they were whole numbers. Then place the decimal in the answer under the decimal points in the given numbers.
- Multiply Decimals
- Determine the sign of the product.
- Write in vertical format, lining up the numbers on the right. Multiply the numbers as if they were whole numbers, temporarily ignoring the decimal points.
- Place the decimal point. The number of decimal places in the product is the sum of the decimal places in the factors.
- Write the product with the appropriate sign.
- Multiply a Decimal by a Power of Ten
- Move the decimal point to the right the same number of places as the number of zeros in the power of 10.
- Add zeros at the end of the number as needed.
- Divide Decimals
- Determine the sign of the quotient.
- Make the divisor a whole number by “moving” the decimal point all the way to the right. “Move” the decimal point in the dividend the same number of places – adding zeros as needed.
- Divide. Place the decimal point in the quotient above the decimal point in the dividend.
- Write the quotient with the appropriate sign.
- Convert a Decimal to a Proper Fraction
- Determine the place value of the final digit.
- Write the fraction: numerator—the ‘numbers’ to the right of the decimal point; denominator—the place value corresponding to the final digit.
- Convert a Fraction to a Decimal Divide the numerator of the fraction by the denominator.
1.4 Exercise Set
In the following exercises, round each number to the nearest tenth.
- 0.67
- 2.84
In the following exercises, round each number to the nearest hundredth.
- 0.845
- 0.299
- 4.098
- 5.781
- 63.479
In the following exercises, add or subtract.
In the following exercises, multiply.
In the following exercises, write each decimal as a fraction.
- 0.04
- 0.52
- 1.25
- 0.375
- 0.095
- Salary Increase. Marta got a raise and now makes $58,965.95 a year. Round this number to the nearest
a) dollar
b) thousand dollars
c) ten thousand dollars. - Sales Tax. Hyo Jin lives in Vancouver. She bought a refrigerator for $1,624.99 and when the clerk calculated the sales tax it came out to exactly $142.186625. Round the sales tax to the nearest
a) penny and
b) dollar. - Paycheck. Annie has two jobs. She gets paid $14.04 per hour for tutoring at Community College and $8.75 per hour at a coffee shop. Last week she tutored for 8 hours and worked at the coffee shop for 15 hours.
a) How much did she earn?
b) If she had worked all 23 hours as a tutor instead of working both jobs, how much more would she have earned?
Glossary
- decimal
- A decimal is another way of writing a fraction whose denominator is a power of ten.
- repeating decimal
- A repeating decimal is a decimal in which the last digit or group of digits repeats endlessly.
Answers:
- 0.7
- 2.8
- 0.85
- 0.30
- 4.10
- a) 5.78 b) 5.8 c) 6
- a) 63.48 b) 63.5 c) 63
- 24.48
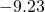
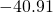
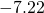
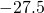
- 15.73
- 102.212
- 51.31
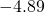
- 0.144
- 42.008
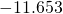
- 337.8914
- 1.305
- 92.4
- 55,200
- 0.19
- $2.44
- 3
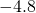
- 35
- 2.08
- 20

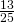
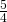
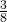
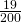
- 0.85
- 2.75
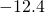
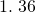
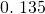
- 3.025
- a) $58,966 b) $59,000 c) $60,000
- a) $142.19; b) $142
- a) $243.57 b) $79.35
Attributions
This chapter has been adapted from “Decimals” in Elementary Algebra (OpenStax) by Lynn Marecek and MaryAnne Anthony-Smith, which is under a CC BY 4.0 Licence. Adapted by Izabela Mazur. See the Copyright page for more information.