6. Health Option
6.1 Measurement; Health Applications
Learning Objectives
By the end of this section it is expected that you will be able to:
- Make unit conversions in the imperial system
- Make unit conversions in the metric system
- Convert between the imperial and the metric systems of measurement
- Convert between Fahrenheit and Celsius temperatures
Make Unit Conversions in the Imperial System
There are two systems of measurement commonly used around the world. Metric system used by most countries and imperial system used by the United States. Even though since 1970, Canada tried to switch to the metric system, the imperial system of measurements is still used in Canada. We will look at the imperial system first.
The imperial system of measurement uses units of inch, foot, yard, and mile to measure length and pound and ton to measure weight. For capacity, the units used are cup, pint, quart, and gallons. Both the imperial system and the metric system measure time in seconds, minutes, and hours.
The equivalencies of measurements are shown in the table below. The table also shows, in parentheses, the common abbreviations for each measurement.
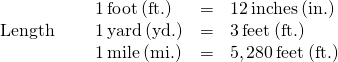 |
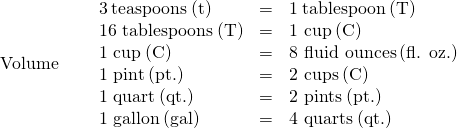 |
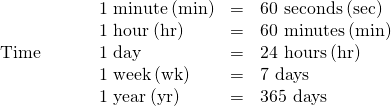 |
In many medical applications, we need to convert between units of measurement, such as feet and inches, minutes and seconds, pounds and ounces, etc. We will use the identity property of multiplication to do these conversions. We’ll restate the identity property of multiplication here for easy reference.
Identity Property of Multiplication
For any real number ![]() :
:
![]()
![]()
1 is the multiplicative identity.
To use the identity property of multiplication, we write 1 in a form that will help us convert the units. For example, suppose we want to change inches to feet. We know that 1 foot is equal to 12 inches, so we will write 1 as the fraction ![]() . When we multiply by this fraction we do not change the value, but just change the units.
. When we multiply by this fraction we do not change the value, but just change the units.
But ![]() also equals 1. How do we decide whether to multiply by
also equals 1. How do we decide whether to multiply by ![]() or
or ![]() ? We choose the fraction that will make the units we want to convert from divide out. Treat the unit words like factors and “divide out” common units like we do common factors. If we want to convert
? We choose the fraction that will make the units we want to convert from divide out. Treat the unit words like factors and “divide out” common units like we do common factors. If we want to convert ![]() inches to feet, which multiplication will eliminate the inches?
inches to feet, which multiplication will eliminate the inches?

The inches divide out and leave only feet. The second form does not have any units that will divide out and so will not help us.
EXAMPLE 1
MaryAnne is 66 inches tall. Convert her height into feet.




TRY IT 1
Lexie is 30 inches tall. Convert her height to feet.
Show answer
2.5 feet
HOW TO: Make unit conversions
- Multiply the measurement to be converted by 1; write 1 as a fraction relating the units given and the units needed.
- Multiply.
- Simplify the fraction.
- Simplify.
EXAMPLE 2
Eli’s six months son is 102.4 ounces. Convert his weight to pounds.
Solution
To convert ounces into pounds we will multiply by conversion factors of 1.
| 102.4 ounces | |
| Write 1 as |
|
| Divide out the common units. | |
| Simplify the fraction. | |
| Simplify. |
Eli’s six months son weights 6.4 pounds.
TRY IT 2
One year old girl weights 11 pounds. Convert her weight to ounces.
Show answer
176 ounces.
When we use the identity property of multiplication to convert units, we need to make sure the units we want to change from will divide out. Usually this means we want the conversion fraction to have those units in the denominator. Sometimes, to convert from one unit to another, we may need to use several other units in between, so we will need to multiply several fractions.
EXAMPLE 3
How many ounces are in 1 gallon?
We will convert gallons to ounces by multiplying by several conversion factors. Refer to the table on Imperial Systems of Measurement.
| 1 gallon | |
| Multiply the measurement to be converted by 1. | |
| Use conversion factors to get to the right unit. Simplify. |
|
| Multiply. | |
| Simplify. | There are 128 ounces in a gallon. |
TRY IT 3
How many teaspoons are in 1 cup?
Show answer
48 teaspoons
Make Unit Conversions in the Metric System
In the metric system, units are related by powers of 10. The roots words of their names reflect this relation. For example, the basic unit for measuring length is a metre. One kilometre is 1,000 metres; the prefix kilo means thousand. One centimetre is ![]() of a metre, just like one cent is
of a metre, just like one cent is ![]() of one dollar.
of one dollar.
The equivalencies of measurements in the metric system are shown in the table below. The common abbreviations for each measurement are given in parentheses.
| Length | Mass | Capacity |
|---|---|---|
| 1 kilometre (km) = 1,000 m | 1 kilogram (kg) = 1,000 g | 1 kilolitre (kL) = 1,000 L |
| 1 hectometre (hm) = 100 m | 1 hectogram (hg) = 100 g | 1 hectolitre (hL) = 100 L |
| 1 dekametre (dam) = 10 m | 1 dekagram (dag) = 10 g | 1 dekalitre (daL) = 10 L |
| 1 metre (m) = 1 m | 1 gram (g) = 1 g | 1 litre (L) = 1 L |
| 1 decimetre (dm) = 0.1 m | 1 decigram (dg) = 0.1 g | 1 decilitre (dL) = 0.1 L |
| 1 centimetre (cm) = 0.01 m | 1 centigram (cg) = 0.01 g | 1 centilitre (cL) = 0.01 L |
| 1 millimetre (mm) = 0.001 m | 1 milligram (mg) = 0.001 g | 1 millilitre (mL) = 0.001 L |
| 1 microgram ( mcg) = 0.000001 g | ||
| 1 metre = 100 centimetres | 1 gram = 100 centigrams | 1 litre = 100 centilitre s |
| 1 metre = 1,000 millimetres | 1 gram = 1,000 milligrams | 1 litre = 1,000 millilitre s |
To make conversions in the metric system, we will use the same technique we did in the Imperial system. Using the identity property of multiplication, we will multiply by a conversion factor of one to get to the correct units.
EXAMPLE 4
Samadia took 800mg of Ibuprofen for her inflammation. How many grams of Ibuprofen did she take?
We will convert milligrams to grams using the identity property of multiplication.
| 800 milligrams | |
| Multiply the measurement to be converted by 1. | 800 milligrams × 1 |
| Write 1 as a fraction relating kilometres and metres. | |
| Simplify. | |
| Multiply. | 0.8 grams |
| Samadia took 0.8 grams of Ibuprofen. |
TRY IT 4
Klaudia took 0.125 grams of Ibuprofen for his headache. How many milligrams of the medication did she take?
Show answer
125 milligrams
EXAMPLE 5
Eleanor’s newborn baby weighed 3,200 grams. How many kilograms did the baby weigh?
We will convert grams into kilograms.
 |
|
| Multiply the measurement to be converted by 1. |  |
| Write 1 as a function relating kilograms and grams. | 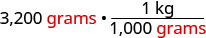 |
| Simplify. | 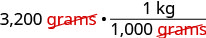 |
| Multiply. | |
| Divide. | 3.2 kilograms The baby weighed 3.2 kilograms. |
TRY IT 5
Kari’s newborn baby weighed 2,800 grams. How many kilograms did the baby weigh?
Show answer
2.8 kilograms
As you become familiar with the metric system you may see a pattern. Since the system is based on multiples of ten, the calculations involve multiplying by multiples of ten. We have learned how to simplify these calculations by just moving the decimal.
To multiply by 10, 100, or 1,000, we move the decimal to the right one, two, or three places, respectively. To multiply by 0.1, 0.01, or 0.001, we move the decimal to the left one, two, or three places, respectively.
We can apply this pattern when we make measurement conversions in the metric system. In Example 8, we changed 3,200 grams to kilograms by multiplying by ![]() (or 0.001). This is the same as moving the decimal three places to the left.
(or 0.001). This is the same as moving the decimal three places to the left.
EXAMPLE 6
The volume of blood coursing throughout an adult human body is about 5 litres. Convert it to millilitres.
We will convert litres to millilitres. In the Metric System of Measurement table, we see that ![]()
| Multiply by 1, writing 1 as a fraction relating litres to millilitres. | |
| Simplify. | |
| Multiply. |
TRY IT 6
Convert 6.3 L to millilitre
Show answer
6,300 millilitres
Convert Between the Imperial and the Metric Systems of Measurement
As Canada uses both system of measurement, we need to be able to convert between the two systems.
The table below shows some of the most common conversions.
| Length | Mass | Capacity |
|---|---|---|
 |
 |
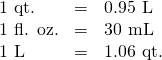 |
(Figure.2) shows how inches and centimetres are related on a ruler.

(Figure.3) shows the ounce and millilitre markings on a measuring cup.
(Figure.4) shows how pounds and kilograms marked on a bathroom scale.

We make conversions between the systems just as we do within the systems—by multiplying by unit conversion factors.
EXAMPLE 7
Plastic bag used for transfusion holds 500 mL of packed red cells. How many ounces are in the bag? Round to the nearest tenth of an ounce.
| 500 mL | |
| Multiply by a unit conversion factor relating mL and ounces. | |
| Simplify. | |
| Divide. | 16.7 ounces. |
| The plastic bag has 16.7 ounces of packed red cells. |
TRY IT 7
Adam donated 450 ml of blood. How many ounces is that?
Show answer
15 ounces.
EXAMPLE 8
A human brain weights about 3 pounds. How many kilograms is that? Round to the nearest tenth of a kilogram.
| 3 pounds | |
| Multiply by a unit conversion factor relating km and mi. | |
| Simplify. | |
| Divide. | 1.4 kilograms |
| A human brain weights around 1.4 kilograms. |
TRY IT 8
A human liver normally weights approximately 1.5 kilograms. Convert it to pounds.
Show answer
3.3 pounds
Convert between Fahrenheit and Celsius Temperatures
Have you ever been in a foreign country and heard the weather forecast? If the forecast is for ![]() °F what does that mean?
°F what does that mean?
The Canadian and imperial systems use different scales to measure temperature. The Canadian system uses degrees Celsius, written °C. The imperial system uses degrees Fahrenheit, written°F. (Figure.5) shows the relationship between the two systems.
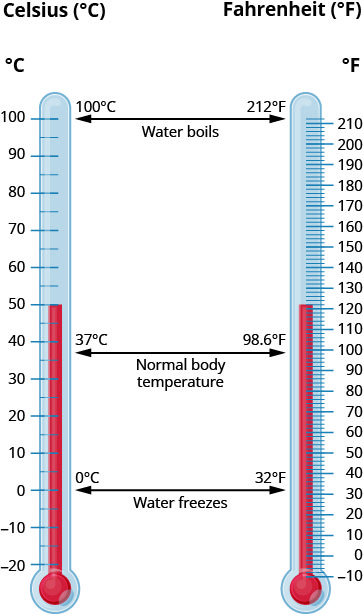
Temperature Conversion
To convert from Fahrenheit temperature, F, to Celsius temperature, C, use the formula
![]() .
.
To convert from Celsius temperature, C, to Fahrenheit temperature, F, use the formula
![]() .
.
EXAMPLE 9
Before mixing, the Pfizer-BioNTech COVID-19 vaccine may be stored in an ultra-cold freezer between -112°F and -76°F. Convert the temperatures into degrees Celsius.
Solution
We will substitute a) -112°F and b) -76°F into the formula to find C.
| a) Substitute -112 for F | |
| Simplify in parentheses. | |
| Multiply. | C= – 80
So we found that -112°F is equivalent to -80°C |
| b) Substitute -76 for F | |
| Simplify. | C= – 60 So we found that -76°F is equivalent to – 60°C.
|
TRY IT 9
Convert the Fahrenheit temperature to degrees Celsius: 59° Fahrenheit.
Show answer°C
15°C
EXAMPLE 10
Once mixed, the Pfizer-BioNTech COVID-19 vaccine can be left at room temperature 2°C to 25°C. Convert the temperatures into degrees Fahrenheit.
Solution
We will substitute a) 2°C and b) 25°C into the formula to find F.
| a) Substitute 2 for C | |
| Simplify. | F= 35.6
So we found that 2°C is equivalent to 35.6°F. |
| b) Substitute 25 for C | |
| Simplify. | F= 77 |
| So we found that 25°C is equivalent to 77°F. |
TRY IT 10
Patient with high fever had a temperature of 39° Celsius. Convert it to Fahrenheit.
Show answer
102.2°F
Key Concepts
- Metric System of Measurement
- Length

- Mass

- Capacity

- Length
- Temperature Conversion
- To convert from Fahrenheit temperature, F, to Celsius temperature, C, use the formula
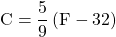
- To convert from Celsius temperature, C, to Fahrenheit temperature, F, use the formula
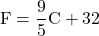
- To convert from Fahrenheit temperature, F, to Celsius temperature, C, use the formula
6.1 Exercise Set
In the following exercises, convert the units.
- A basketball player is 6 feet tall. Convert his height to inches.
- Kelvin is 18 inches tall. Convert his height to feet.
- Doctor recommended a patient to walk 1.5 miles every other day. Convert the distance to feet.
- Misty’s surgery lasted
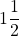 hours. Convert the time to seconds.
hours. Convert the time to seconds. - How many teaspoons are in a pint?
- Jon is 6 feet 4 inches tall. Convert his height to inches.
- Baby Preston weighed 7 pounds 3 ounces at birth. Convert his weight to ounces.
In the following exercises, convert the units.
- Ryan ran 5 kilometres. Convert the length to metres.
- Emily is 1.55 metres tall. Convert her height to centimetres.
- June’s multivitamin contains 1,500 milligrams of calcium. Convert this to grams.
- One stick of butter contains 91.6 grams of fat. Convert this to milligrams.
- Dimitri’s daughter weighed 3.8 kilograms at birth. Convert this to grams
- A bottle of medicine contained 300 millilitres. Convert this to litres.
In the following exercises, solve.
- Matthias is 1.8 metres tall. His son is 89 centimetres tall. How much taller is Matthias than his son?
- One glass of orange juice provides 560 milligrams of potassium. Linda drinks one glass of orange juice every morning. How many grams of potassium does Linda get from her orange juice in 30 days?
- Jonas drinks 200 millilitres of water 8 times a day. How many litres of water does Jonas drink in a day?
In the following exercises, make the unit conversions. Round to the nearest tenth.
- Bill is 75 inches tall. Convert his height to centimetres.
- Kathryn is 1.6 metres tall. Convert her height to feet
In the following exercises, convert the Fahrenheit temperatures to degrees Celsius. Round to the nearest tenth.
- 86° Fahrenheit
- 104° Fahrenheit
- 72° Fahrenheit
- 0° Fahrenheit
In the following exercises, convert the Celsius temperatures to degrees Fahrenheit. Round to the nearest tenth.
- 5° Celsius
- -10° Celsius
- 22° Celsius
- 43° Celsius
Everyday Math
- Nutrition Julian drinks one can of soda every day. Each can of soda contains 40 grams of sugar. How many kilograms of sugar does Julian get from soda in 1 year?
Answers
- 72 inches
- 1.5 feet
- 7,920 feet
- 5,400 s
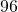 teaspoons
teaspoons- 76 in.
- 115 ounces
- 5,000 metres
- 155 centimetres
- 1.5 grams
- 91,600 milligrams
- 3,800 grams
- 0.3 litres
- 91 centimetres
- 16.8 grams
- 1.6 litres
- 190.5 centimetres
- 5.2 feet
- 30°C
- 40°C
- 22.2°C
- -17.8°C
- 41°F
- 14°F
- 71.6°F
- 109.4°F
- 14.6 kilograms
Attributions
- This chapter has been adapted from “Systems of Measurement” in Elementary Algebra (OpenStax) by Lynn Marecek and MaryAnne Anthony-Smith, which is under a CC BY 4.0 Licence. Adapted by Izabela Mazur. See the Copyright page for more information.
- OER.hawaii.edu
- COVID-19 Government of Canada website https://www.canada.ca/en/health-canada/news/2021/05/health-canada-authorizes-more-flexible-storage-conditions-for-pfizer-biontech-covid-19-vaccine.html

