5.4 Silicate Minerals
Silicon and oxygen bond covalently to create a silicate tetrahedron (SiO44-), which is a four-sided pyramid shape with oxygen at each corner and silicon in the middle (Figure 5.21). This structure is the building block of many important minerals in the crust and mantle. Silicon has a charge of +4, and oxygen has a charge of -2, so the total charge of the silicate anion is -4.
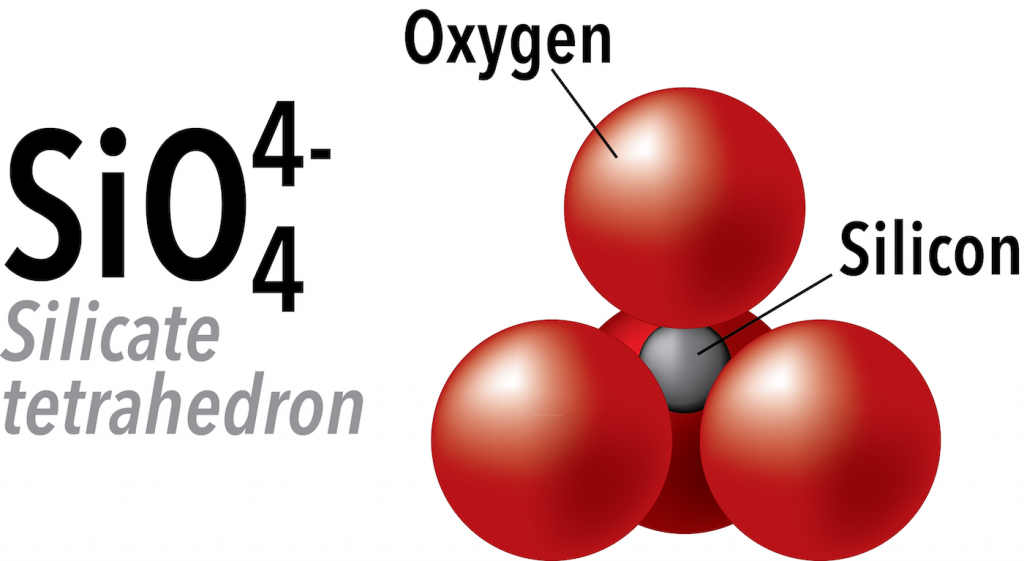
In silicate minerals, these tetrahedra are arranged and linked together in a variety of ways, from single units to chains, rings, and more complex frameworks. In the rest of this section we will look at the structures of the most common silicate minerals in Earth’s crust and mantle.
Make Your Own Tetrahedron
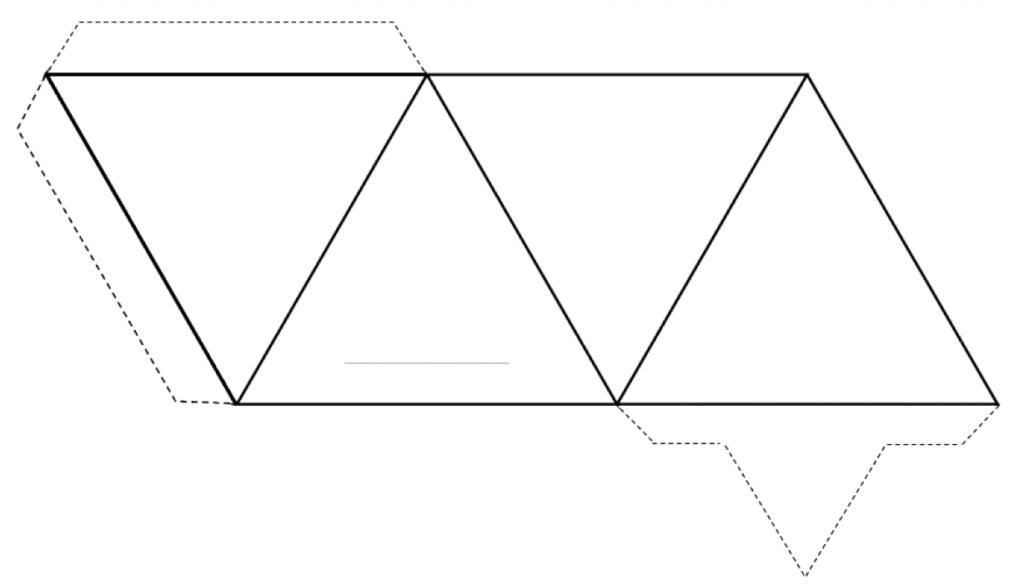
Download Tetrahedron [PDF] with the tetrahedron pattern shown here. Cut around the outside of the shape (solid lines and dotted lines), and then fold along the solid lines to form a tetrahedron.
If you have glue or tape, secure the tabs to the tetrahedron to hold it together. If you don’t have glue or tape, make a slice along the thin grey line and insert the pointed tab into the slit.
If you’re feeling ambitious, make several tetrahedra and and use toothpicks through the corners to make the configurations discussed below.
Isolated Tetrahedra
The simplest silicate structure—that of the mineral olivine (Figure 5.23)—is composed of isolated tetrahedra bonded to iron and/or magnesium ions. In olivine, the –4 charge of each silica tetrahedron is balanced by two iron or magnesium cations, each with a charge of +2.

Olivine can be pure Mg2SiO4 or pure Fe2SiO4, or a combination of the two, written as (Mg,Fe)2SiO4. Magnesium and iron can substitute for each other because they both have a charge of +2, and they are similar in size: magnesium cations have a radius of 0.73 Å, and iron cations have a radius of 0.62 Å [1].
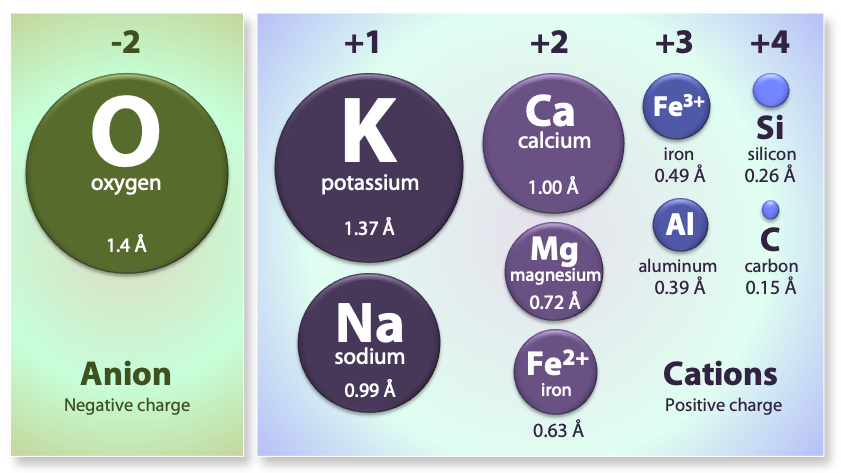
While iron and magnesium ions are similar in size, allowing them to substitute for each other in some silicate minerals, the common ions in silicate minerals come in a wide range of sizes (Figure 5.24). Ionic radii are critical to the composition of silicate minerals, because the structure of the silicate mineral will determine the size of spaces available.
Chain Silicates
The mineral pyroxene is an example of a single-chain silicate (Figure 5.25), where one oxygen from each tetrahedron is shared with the next tetrahedron. Sharing means that fewer oxygens are needed to make the tetrahedra, so there’s less oxygen in this structure over all compared to olivine. This can be expressed as a silicon-to-oxygen ratio (Si:O). In olivine, tetrahedra aren’t connected directly to each other, so each silicon atom must have four oxygen atoms all to itself to complete a tetrahedron. That’s a ratio of 1:4. In pyroxene, each silicon atom only needs three unique oxygen atoms because it can borrow one from a neighbour to have a tetrahedron. For pyroxene, the Si:O is 1:3. With one less oxygen in the mix per tetrahedron, the net charge per silicon atom that must be balanced by cations is lower (-2 instead of -4).

The way tetrahedra share oxygens in single-chain silicates is why, even though pyroxene is built out of silicate tetrahedra (with the silicate anion being SiO44-), its formula has the tetrahedra represented as SiO3 (e.g., MgSiO3, FeSiO3, and CaSiO3[2], or a multiple thereof). In other words, pyroxene has one cation for each silica tetrahedron (e.g., MgSiO3) while olivine has two (e.g., Mg2SiO4).
The structure of pyroxene is also more “permissive” than that of olivine, meaning cations with a wider range of ionic radii can fit into it. That’s why pyroxenes can have calcium cations (radius 1.00 Å) substitute for iron (0.63 Å) and magnesium (0.72 Å).
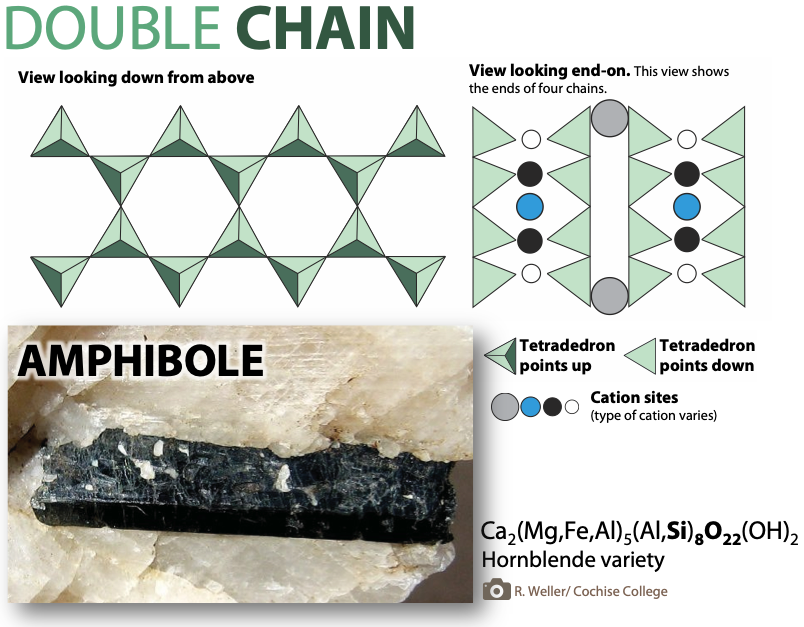
The mineral amphibole is also a chain silicate, but the the silica tetrahedra are linked in a double chains (Figure 5.26). Amphibole has a silicon-to-oxygen ratio higher than that of pyroxene, and hence still fewer cations are necessary to balance the charge. Amphibole is even more permissive than pyroxene, and its compositions can be very complex.
Can You Find the Silicon to Oxygen Ratios?
Two chain silicate structures are shown below. For both, the smallest segment possible that can be repeated to get the chain, is highlighted. Refer to the highlights to verify for yourself the Si:O ratio of pyroxene (single chain) and to figure out the Si:O ratio of amphibole (double chain).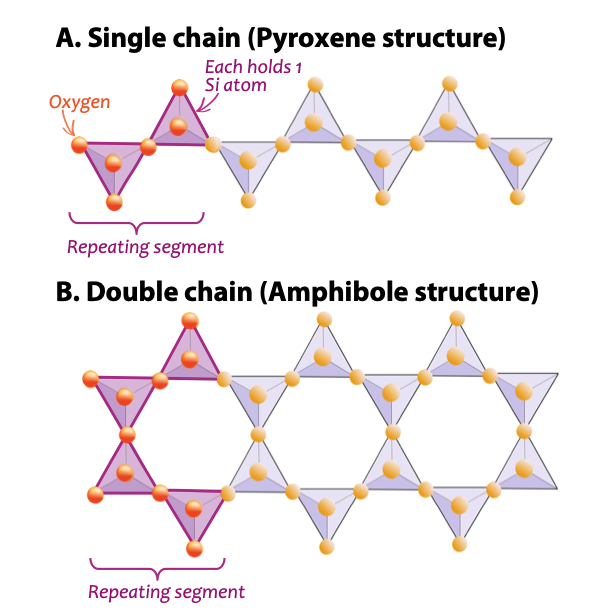
- Single chain: Pyroxene structure.
- How may tetrahedra are highlighted?
- How many oxygen atoms are highlighted?
- This gives a Si:O ratio of : . Note: Remember to reduce your fraction. E.g., [latex]\tfrac{2}{4}[/latex] is the same as [latex]\tfrac{1}{2}[/latex].
- B. Double chain: Amphibole structure.
- How may tetrahedra are highlighted?
- How many oxygen atoms are highlighted?
- This gives a Si:O ratio of : .
To check your answers, navigate to the below link to view the interactive version of this activity.
Sheet Silicates
In mica structures, the silica tetrahedra are arranged in continuous sheets (Figure 5.27), where each tetrahedron shares three oxygen anions with adjacent tetrahedra. Because even more oxygens are shared between adjacent tetrahedra, fewer charge-balancing cations are needed for sheet silicate minerals.
Bonding between sheets is relatively weak, and this accounts for the tendency of mica minerals to split apart in sheets (Figure 5.27 bottom right). Two common micas in silicate rocks are biotite (Figure 5.27 bottom left), which contains iron and/or magnesium, making it a dark mineral; and muscovite (Figure 5.27 right), which contains aluminum and potassium, and is light in colour. All of the sheet silicate minerals have water in their structure, in the form of the hydroxyl (OH-) anion.
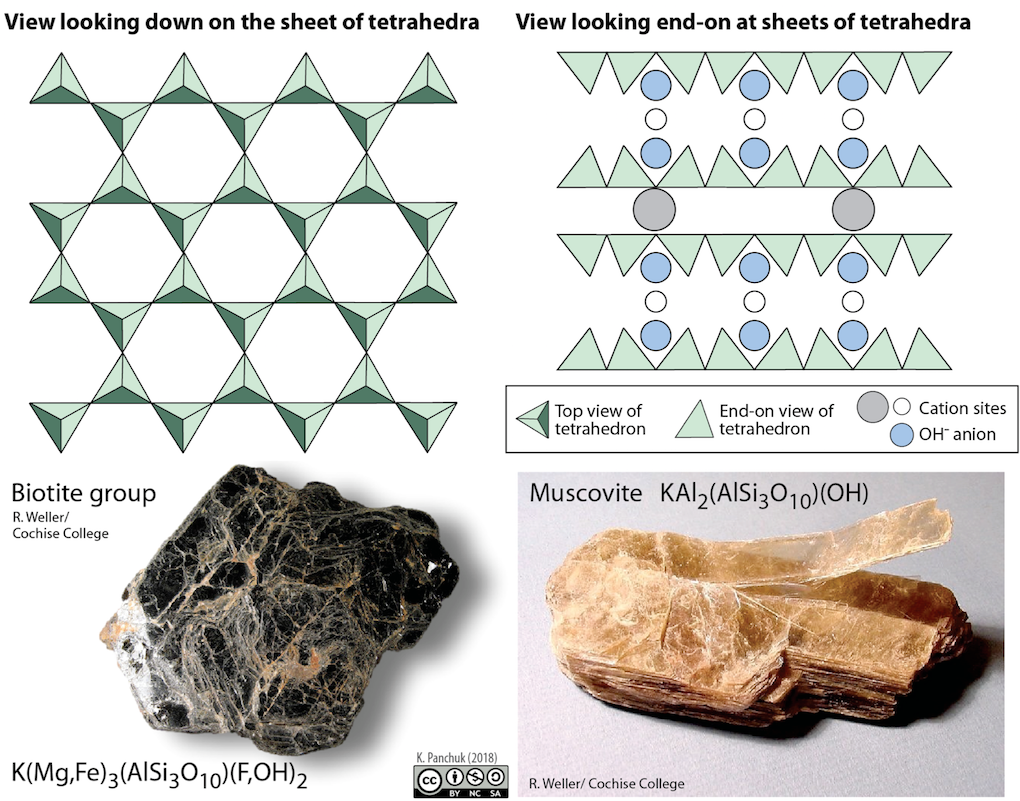
Some sheet silicates typically occur in clay-sized fragments (i.e., less than 0.004 mm). These include the clay minerals kaolinite, illite, and smectite, which are important components of rocks and especially of soils.
Framework Silicates
In framework silicates, tetrahedra are connected to each other in three-dimensional structures rather than in two-dimensional chains and sheets.
Feldspar
Feldspars are a group of very abundant framework silicates in Earth’s crust. They include alumina tetrahedra as well as silicate tetrahedra. In alumina tetrahedra, there is an aluminum cation at the centre instead of a silicon cation.
Feldspars are classified using a ternary (3-fold) system with three end-members (“pure” feldspars). This system is illustrated with a triangular diagram that has each end-member at one corner (Figure 5.28). The distance along a side of the diagram represents the relative abundance of the composition of each end-member.
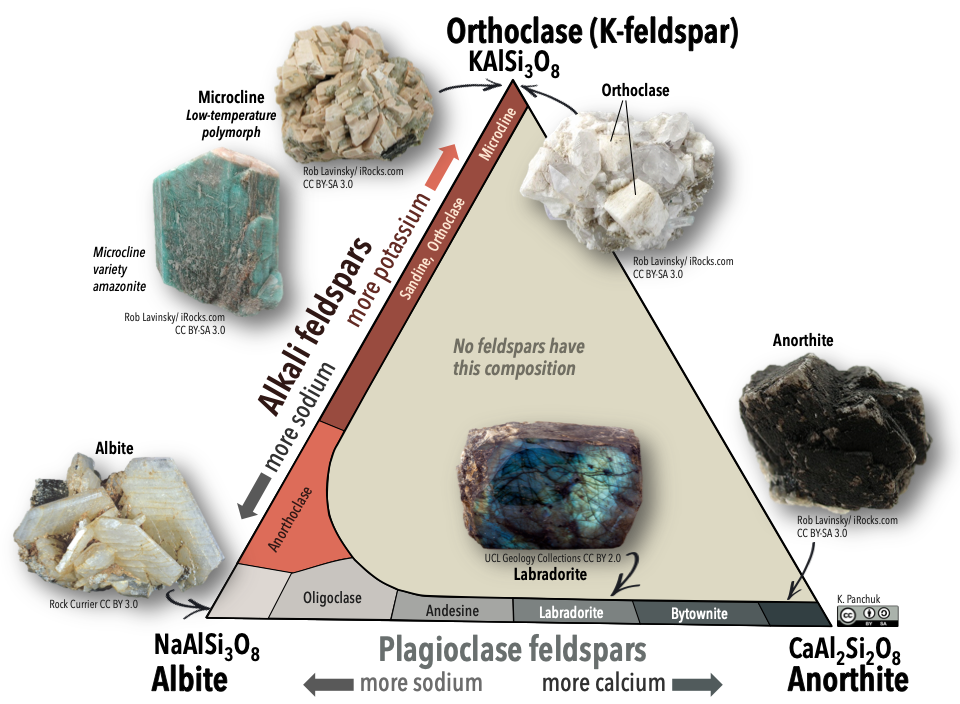
One end-member is potassium feldspar (also referred to as K-feldspar), which has the composition KAlSi3O8. Depending on the temperature and rate of cooling, K-feldspar can occur as one of three polymorphs: orthoclase, sanidine, or microcline. Another end member is albite, which has sodium instead of potassium (formula NaAlSi3O8). As is the case for iron and magnesium in olivine, there is a continuous range of compositions (referred to as a solid-solution series) between albite and orthoclase. Feldspars in this series are referred to as alkali feldspars. Potassium cations are much larger than sodium cations (1.37 Å versus 0.99 Å, respectively), so high temperatures are required to form alkali feldspars with intermediate compositions.
The third end-member is anorthite and it has calcium instead of potassium or sodium (formula CaAl2Si3O8). Feldspars in the solid-solution series between albite and anorthite are called plagioclase feldspars. Calcium and sodium cations are nearly the same size (1.00 Å and 0.99 Å, respectively), so from that perspective it makes sense that they substitute readily for each other, and that any intermediate compositions between CaAl2Si3O8 and NaAlSi3O8 can exist. However, calcium and sodium ions don’t have the same charge (Ca2+ versus Na+), making it surprising that they substitute so easily. The difference in charge is accommodated by substituting some Al3+ for Si4+. Albite has one Al and three Si in its formula, while anorthite is has two Al and two Si. Plagioclase feldspars of intermediate composition also have intermediate proportions of Al and Si.
Quartz
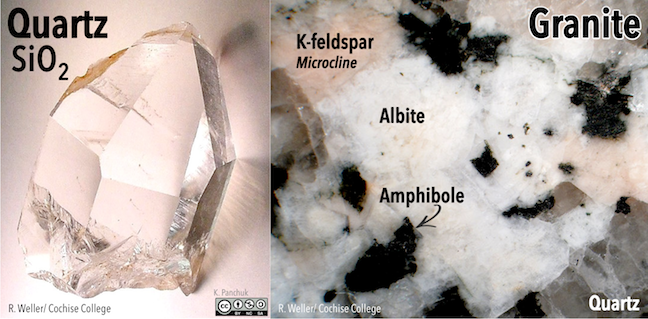
Quartz (SiO2; Figure 5.29) contains only silica tetrahedra. In quartz, each silica tetrahedron is bonded to four other tetrahedra (with an oxygen shared at every corner of each tetrahedron), making a three-dimensional framework. As a result, the ratio of silicon to oxygen is 1:2. Because the one silicon cation has a +4 charge and the two oxygen anions each have a –2 charge, the charge is balanced. There is no need to add cations to balance the charge. The hardness of quartz and the fact that it breaks irregularly (notice the bottom of the crystal in Figure 5.29 right) and not along smooth planes result from the strong covalent/ionic bonds characteristic of the silica tetrahedron.
Practice with Silicate Minerals & Their Structures
Download a printable version of this exercise: Silicate Minerals & Their Structures [PDF].
The original version of this chapter contained H5P content. You may want to remove or replace this element.
References
Klein, C. & Hurlbut, C. S., Jr. (1993). Manual of mineralogy (after J. D. Dana). John Wiley & Sons, Inc.

